向量间距离
在初中学习过绝对值,数轴上两个点的距离,可以用绝对值表示。
即两点的距离 d=∣x2−x1∣
比如A=1,B=−2,则∣AB∣=∣1−(−2)∣=3
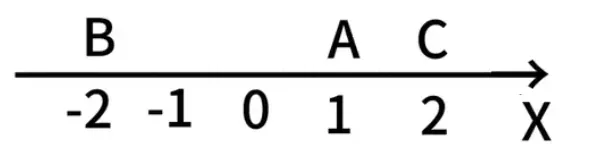 {width=300px}
同样,可以定义两个向量间的距离,但是通常称为距高。
{width=300px}
同样,可以定义两个向量间的距离,但是通常称为距高。
Rn 中向量 u 和 v 的距高, 记作 dist(u,v), 表示向量 u−v 的长度, 即
dist(u,v)=∥u−v∥ 向量行距的几何意义
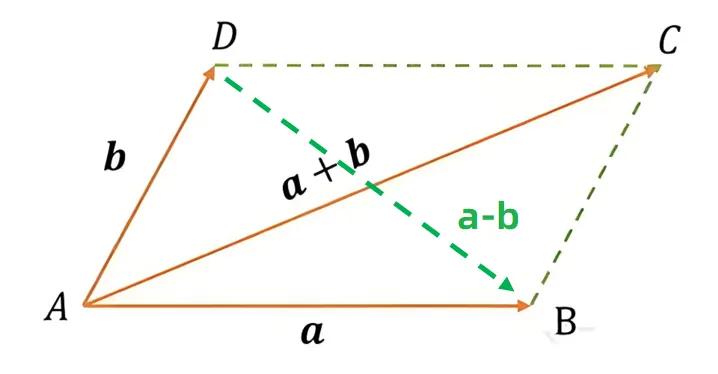
假设有两个向量a,b, 根据向量的平行四边形法则,a+b 表示的是一条主对角线,而 a−b 表示的是一条副对角线。
所以,两个向量的距离就是 幅对角线的长度。
 {width=400px}
{width=400px}
例题
例 计算向量 u=(7,1) 和 v=(3,2) 之间的距离。
解 先计算 u−v=[71]−[32]=[4−1], 则有 ∥u−v∥=42+(−1)2=17.
例 如果 u=(u1,u2,u3) 和 v=(v1,v2,v3), 那么
dist(u,v)=∥u−v∥=(u−v)⋅(u−v)=(u1−v1)2+(u2−v2)2+(u3−v3)2 例 α=[1,1,1]T,β=[3,2,3]T ,求 α,β 之间的距离、夹角以及与 α 同方向的单位向量.
解 ∥α∥=(α,α)=3,∥β∥=(β,β)=22,(α,β)=8,α−β=−2−1−2 ,
故
∥α−β∥=(α−β,α−β)=3cosθ=∥α∥⋅∥β∥(α,β)=668=33466 所以
θ=arccos33466 令
η=∥α∥1⋅α=31111 显然,∥η∥=1 且 η 与 α 同方向.
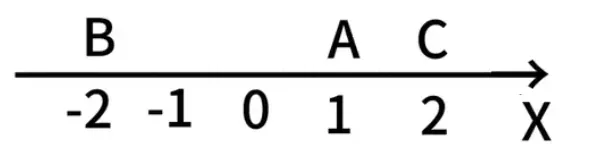 {width=300px}
同样,可以定义两个向量间的距离,但是通常称为距高。
{width=300px}
同样,可以定义两个向量间的距离,但是通常称为距高。 {width=400px}
{width=400px}