7._向量投影 - 线性代数

二维投影

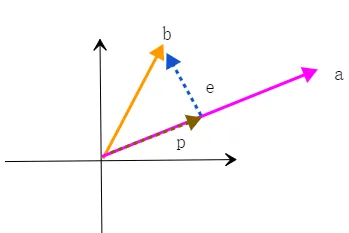
向量投影是向量空间到自身的线性变换。例如在二维平面上，有两个向量 $a$ 和 $b$ 。向量 $b$ 在向量 $a$ 上的投影，是自 $b$ 向 $a$ 做垂线，我们把这个投影向量命名为 $p$ 。

由于 $p$ 是投影到 $a$ 上的，所以我们可以用某个常数系数 $x$ 来表示 $p$ 相对于 $a$ 的位置。

此外，我们还可以定义另一个向量 $e$ ，它与 $a$ 正交如下图。如果把所有关系都写下来，就会变成这样。

$图片$

根据高中向量平面向量的运行性质，很容易得出下面的性质

(1) $\vec{p}=x \vec{a}$ ( $x$ 为常数，向量共线定理) (2) $\vec{e}=\vec{b}-\vec{p}$ (向量减法的三角形法则详见此处) (3) $\vec{a} \vec{e}=0$ (向量正交定义,几何意义详见此处)

由了上面的三个等式后，我们的目标是投影向量 $p$ 能用 $a,b$ 向量表示。把(1)(2)(3)当做普通方程来解即可。

答案如下: ① 将 (1) 带入 (2) : $\vec{e}= \vec{b}-x\vec{a}$ ...(4)

②将(4)带入(3)得:

$\vec{a}(\vec{b}-x \vec{a}) =0$ 即

$\vec{a} \vec{b}-\vec{a} x \vec{a} =0$

③因为 $x$ 为常数,可以提取到前面

\vec{a} \vec{b}-x \vec{a} \vec{a}=0

即得到

x=\dfrac{\vec{a} \vec{b}}{\vec{a} \vec{a}} ...(5)

将(5)带入(1)式得

\boxed{ p =\dfrac{\vec{a} \vec{b}}{\vec{a} \vec{a}} {\vec{a}} ...(1.1) }

这就是投影公式，要完全理解这个等式可能比较困难，下面让我举一个具体的例子就明白了。

举例

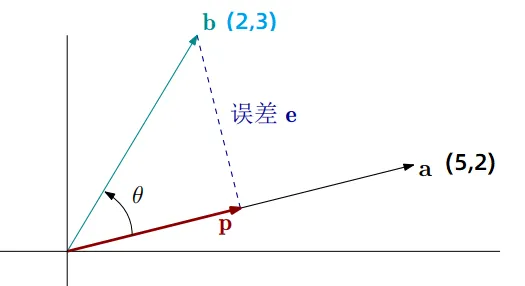
假设有两个向量: $\boldsymbol{a}=(5,2)$ 和 $\boldsymbol{b}=(2,3)$ 计算 $b$ 在 $a$ 上的投影。

$图片$ {width=350px}

我们先计算一下 $x=\dfrac{\boldsymbol{a b}}{\boldsymbol{a a}}$ 因为两个向量内积，为两个向量坐标分量直接乘积，所以， $\boldsymbol{ab}=5*2+2*3=16$ $\boldsymbol{aa}=5^2+2^2=29$

所以 $x=\dfrac{16}{29}$

所以 $p=x\boldsymbol{a}= \dfrac{16}{29} (5,2)= (\dfrac{80}{29},\dfrac{32}{29})$

现在你可以看到，投影向量 $p$ 只不过是向量 $a$ 的缩放版本。

投影矩阵

给定 $a \in R ^m$ 和 $b \in R ^m$ ，上面我们从向量的角度除非，给出了 $b$ 在 $a$ 上的投影 $p$ 。现在再从矩阵的角度理解这个问题：能否找到一个矩阵 $P$ ，使得我们有：

P\boldsymbol{b}=\boldsymbol{p}

可以证明

P=\dfrac{a a^{\top}}{a^{\top} a}

这里 $P$ 是一个 $m \times m$ 的矩阵。

证明．

Pb=\frac{a a^{\top}}{a^{\top} a} b=\frac{a a^{\top} b}{a^{\top} a}=\frac{a^{\top} b a}{a^{\top} a}=\frac{a^{\top} b}{a^{\top} a} a=p

三维投影

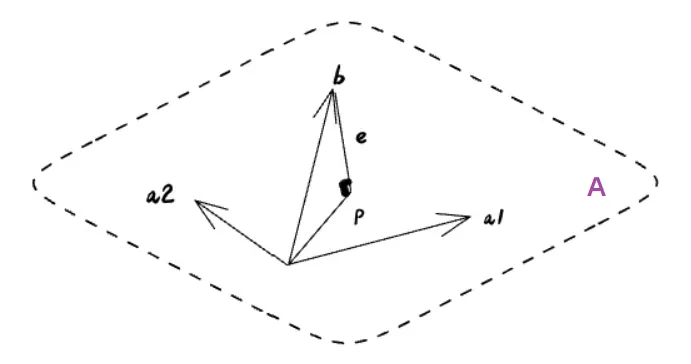
如下图： 1.平面 $A$ 是 $a_1$ 和 $a_2$ 张成的平面。 2. $a_1$ 和 $a_2$ 是 A 的列向量即：

A=\left[\begin{array}{ll} a_1 & a_2 \end{array}\right]

我们看到的平面是一个列空间，由列向量 $a_1$ 和 $a_2$ 表示。 $A$ 是一个矩阵，其中包含了这些列向量。现在我们要做的是将不在这个平面上的向量 $b$ 投影到平面上。

就像在二维示例中一样，我们定义了两个向量 $p$ 和 $e$ 。

$图片$ {width=450px}

1.因为 $p$ 在平面内，所以 $p$ 可以表示为 $a_1, a_2$ 的线性组合， $x_1, x_2$ 为常数

p=A x=x_1 a_1+x_2 a_2

2.在 $b, p$ 平面内，向量 $e$ 依然可以表示为:

e=b-p=b-A x

由于 $e$ 垂直于平面，根据两个向量垂直内积为零，可以建立如下两个方程。

\left\{\begin{array}{l} a_1 e=0 \\ a_2 e=0 \end{array}\right.

将这两个等式合并并进行相应的修改，我们就得到了缩放因子 $x$ . 然后将 $e$ 代入后

\left[\begin{array}{l} a_1 \\ a_2 \end{array}\right](b-A x)=\left[\begin{array}{l} 0 \\ 0 \end{array}\right]

通过解这个方程也可以求得投影P向量。有了上面二维和三维作为铺垫，现在可以推广到 $n$ 维了。

n维向量投影

对 $R ^n$ 中给出的非零向量 $u$ , 考虑 $R ^n$ 中一个向量 $y$ 分解为两个向量之和的问题, 一个向量是向量 $u$ 的数量乘积，另一个向量与 $u$ 垂直。根据向量运算的平行四边形法则，我们期望写成

y=\hat{y}+z ...(1)

其中 $\hat{ y }=\alpha u , \alpha$ 是一个数， $z$ 是一个垂直于 $u$ 的向量，见下图.

对给定数 $\alpha$ , 记 $z= y -\alpha u$ ,则方程（1）可以满足，那么 $y -\hat{ y }$ 和 $u$ 正交的充分必要条件是

0=( y -\alpha u ) \cdot u = y \cdot u -(\alpha u ) \cdot u = y \cdot u -\alpha( u \cdot u )

$图片$

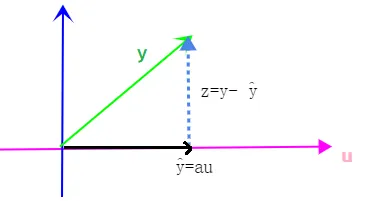
也就是满足方程 (1), 且 $z$ 与 $u$ 正交的充分必要条件是

\boxed{ \alpha=\dfrac{ y \cdot u }{ u \cdot u } }

且

\boxed{ \hat{y}=\dfrac{ y \cdot u }{ u \cdot u } \cdot u }

这就是投影公式。

向量 $\hat{ y }$ 称为 $y$ 在 $u$ 上的正交投影，向量 $z$ 称为 $y$ 垂直 $u$ 的分量.

。有时用 $\operatorname{proj}_L y$ 来表示 $\hat{ y }$ , 并称之为 $y$ 在 $u$ 上的正交投影, 即

\boxed { \hat{y}=\operatorname{proj}_L y=\frac{y \cdot u}{u \cdot u} \cdot u ...(2) }

例题

例 假设 $y =\left[\begin{array}{l}7 \\ 6\end{array}\right]$ 和 $u =\left[\begin{array}{l}4 \\ 2\end{array}\right]$ , 找出 $y$ 在 $u$ 上的正交投影, 然后将 $y$ 写成两个正交向量之和,一个在 $\operatorname{Span}\{ u \}$ , 另一个与 $u$ 正交.

解计算

\begin{aligned} & y \cdot u =\left[\begin{array}{l} 7 \\ 6 \end{array}\right] \cdot\left[\begin{array}{l} 4 \\ 2 \end{array}\right]=40 \\ & u \cdot u =\left[\begin{array}{l} 4 \\ 2 \end{array}\right] \cdot\left[\begin{array}{l} 4 \\ 2 \end{array}\right]=20 \end{aligned}

则 $y$ 在 $u$ 上的正交投影是：

\hat{ y }=\frac{ y \cdot u }{ u \cdot u } \cdot u =\frac{40}{20} u =2\left[\begin{array}{l} 4 \\ 2 \end{array}\right]=\left[\begin{array}{l} 8 \\ 4 \end{array}\right]

$y$ 垂直于 $u$ 的分量是:

y -\hat{ y }=\left[\begin{array}{l} 7 \\ 6 \end{array}\right]-\left[\begin{array}{l} 8 \\ 4 \end{array}\right]=\left[\begin{array}{r} -1 \\ 2 \end{array}\right]

两个向量之和为 $y$ , 即 $图片$

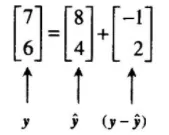
向量 $y$ 的分解可表示为下图. $图片$

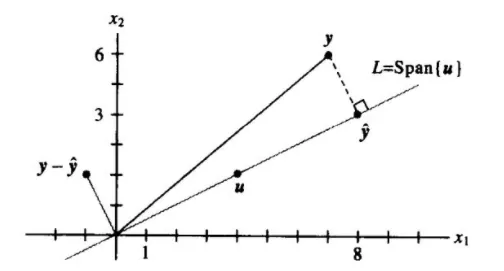
作为检验、计算

\hat{ y } \cdot( y -\hat{ y })=\left[\begin{array}{l} 8 \\ 4 \end{array}\right] \cdot\left[\begin{array}{r} -1 \\ 2 \end{array}\right]=-8+8=0

从高中物理的角度上看，合力y被分解为一个是沿着 $u$ 方向的水平力，一个是沿着 $y-\hat{y}$ 方向上的垂直力。

向量间的距离

由于上图中连接 $y$ 与 $\hat{y}$ 的线段垂直于 $L$ , 由 $\hat{ y }$ 的构造可知, 标记为 $\hat{ y }$ 的点是 $y$ 距离 $L$ 的最近点. (这可用几何方法证明,)

例 计算上例中从 $y$ 到 $L$ 的距离。解从 $y$ 到 $L$ 的距离，是从 $y$ 到正交投影垂直线段的长度，这个长度等于 $y -\hat{y}$ 的长度，从而距离为

\|y-\hat{y}\|=\sqrt{(-1)^2+2^2}=\sqrt{5}

几何解释

对于 $W= R ^2=\operatorname{Span}\left\{u_1, u _2\right\}, u _1$ 和 $u _2$ 相互正交的情形，很容易看到分解式，对任意 $R ^2$ 中的向量 $y$ 可以写成:

y =\frac{ y \cdot u _1}{ u _1 \cdot u _1} u _1+\frac{ y \cdot u _2}{ u _2 \cdot u _2} u _2 ...(3)

（3）中的第一项是 $y$ 在子空间 $\operatorname{Span}\left\{ u _1\right\}$ 上的投影（通过原点和 $u _1$ 的直线），第二项 $y$ 在子空间 Span $\left\{ u _2\right\}$ 上的投影，（3）式将 $y$ 表示为由 $y _1$ 和 $y _2$ 确定的（正交）轴上的投影之和，

$图片$

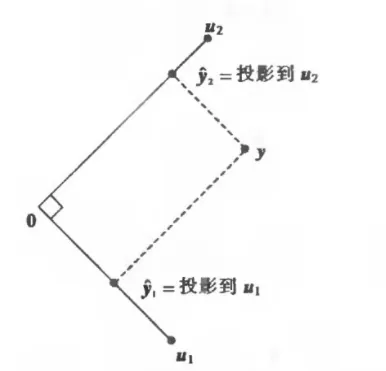
单位正交集

集合 $\left\{ u _1, \cdots, u _p\right\}$ 是一个单位正交集，如果它是由单位向量构成的正交集。如果 $W$ 是一个由单位正交集合组成的子空间，那么 $\left\{ u _1, \cdots, u _p\right\}$ 是 $W$ 的单位正交基，原因是这类集合自然线性无关.

最简单的单位正交集合是 $R ^n$ 中的标准基 $\left\{ e _1, \cdots, e _n\right\}$ , 任何集合 $\left\{ e _1, \cdots, e _n\right\}$ 的非空子集也是单位正交的, 下面是一个更复杂的例子.

例 证明 $\left\{ u _1, u _2, u _3\right\}$ 是 $R ^3$ 的一个单位正交基, 其中:

v _1=\left[\begin{array}{l} 3 / \sqrt{11} \\ 1 / \sqrt{11} \\ 1 / \sqrt{11} \end{array}\right] \quad v _2=\left[\begin{array}{r} -1 / \sqrt{6} \\ 2 / \sqrt{6} \\ 1 / \sqrt{6} \end{array}\right] \quad v _3=\left[\begin{array}{c} -1 / \sqrt{66} \\ -4 / \sqrt{66} \\ 7 / \sqrt{66} \end{array}\right]

解计算

\begin{aligned} & v_1 \cdot v_2=-3 / \sqrt{66}+2 / \sqrt{66}+1 / \sqrt{66}=0 \\ & v_1 \cdot v_3=-3 / \sqrt{726}-4 / \sqrt{726}+7 / \sqrt{726}=0 \\ & v_2 \cdot v_3=1 / \sqrt{396}-8 / \sqrt{396}+7 / \sqrt{396}=0 \end{aligned}

从而 $\left\{ v _1, v _2, v _3\right\}$ 是一个正交基, 另外

\begin{aligned} & v_1 \cdot v_1=9 / 11+1 / 11+1 / 11=1 \\ & v_2 \cdot v_2=1 / 6+4 / 6+1 / 6=1 \\ & v_3 \cdot v_3=1 / 66+16 / 66+49 / 66=1 \end{aligned}

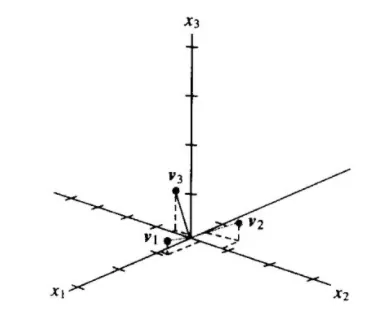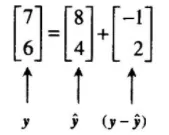
从而证明 $v_1, v_2$ 和 $v_3$ 是单位向量，即 $\left\{v_1, v_2, v_3\right\}$ 是一个单位正交集。由于集合线性无关，它的 $\because$ 个向量构成 $R ^3$ 的一个基, 见图 $图片$ 当一个正交集中的向量被 "单位化" 具有单位长度后, 这些新向量仍然保持正交性, 因此新的集合成为单位正交基