向量的外积 向量外积在本课程里用的很少，稍微了解即可,向量外积表示向量张成的平面有向面积
二维向量的外积 假设有向量 a , b \boldsymbol{a} , \boldsymbol{b} a , b a \boldsymbol{a} a b \boldsymbol{b} b θ \theta θ
a × b = ∣ a ∣ ∣ b ∣ sin θ . . . （二维向量外积） \boxed{
\boldsymbol{a} \times \boldsymbol{b} =| \boldsymbol{a} || \boldsymbol{b} | \sin \theta ...\text{（二维向量外积）}
} a × b = ∣ a ∣∣ b ∣ sin θ ... （二维向量外积） 向量外积表示的是几何意义是：两个向量张成的又向平行四边形的面积 。
对于向量外积，最大的特点是：a × b ≠ b × a a \times b \ne b \times a a × b = b × a ∣ a ∣ ∣ b ∣ sin θ |a| |b| \sin \theta ∣ a ∣∣ b ∣ sin θ sin θ \sin \theta sin θ a a a b b b b b b a a a
a × b = − b × a \boldsymbol{a} \times \boldsymbol{b} = -\boldsymbol{b} \times \boldsymbol{a} a × b = − b × a
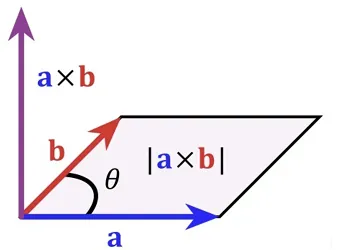
这种方向关系不容易在二维平面上体现，因此一般画成三维图 ，如下图，规定一个方向向上，另外一个乘积的方向就向下，因此外积的方向和a , b a,b a , b
因此，要研究向量外积，就必须先定义三维向量的方向 。
外积的物理意义 向量外积的定义并不是凭空产生，学过高中物理的同学应该都知道 楞次定律 , 通电导线在磁场里运动，会产生力。这里导线的运动v v v B B B f f f v , B , f v,B,f v , B , f f = v t i m e s B f= v times B f = v t im es B
三维向量外积 既然二维向量外积表示2个向量形成的面积，那么三维向量外积就表示3个向量组成的又向空间体积。
左手坐标系和右手坐标系 左手坐标系 对于三维坐标系，一般有两种习俗，左手坐标系和右手坐标系，它们的重点不是在于 z z z z z z
但是如果我们把左手转90°（如下图右图），这依旧是一个左手坐标系
右手坐标系 如下图是右手坐标系。
如下图右图，通过右手旋转90度，这依旧是一个右手坐标系
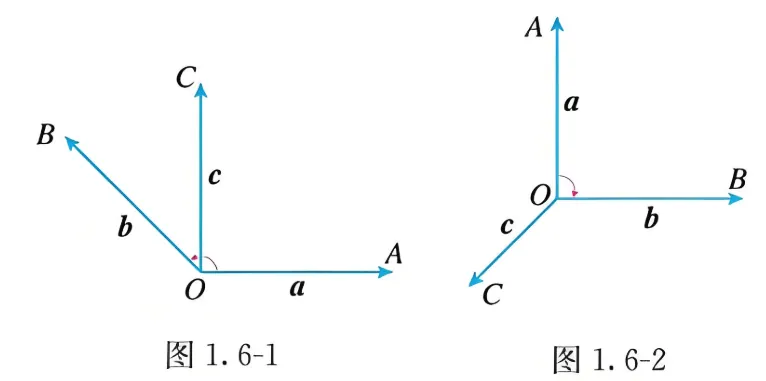
向量的外积 设 { a , b , c } \{\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}\} { a , b , c } V V V O O O O A → = a , O B → = b , O C → = \overrightarrow{O A}=\boldsymbol{a}, \overrightarrow{O B}=\boldsymbol{b}, \overrightarrow{O C}= O A = a , OB = b , OC = c \boldsymbol{c} c a , b , c \boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c} a , b , c a \boldsymbol{a} a b \boldsymbol{b} b c c c { a , b , c } \{\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}\} { a , b , c } a \boldsymbol{a} a b \boldsymbol{b} b c \boldsymbol{c} c { a , b , c } \{\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}\} { a , b , c }
一个基是右手系还是左手系, 与基向量的排列顺序密切相关. 容易验证, 如果 { a , b , c ⃗ } \{\boldsymbol{a}, \boldsymbol{b}, \vec{c}\} { a , b , c } { b , c , a ⃗ } \{\boldsymbol{b}, \boldsymbol{c}, \vec{a}\} { b , c , a } { c , a → , b ⃗ } \overrightarrow{\{c, a}, \vec{b}\} { c , a , b } { b , a → , c ⃗ } , { a , c , b ⃗ } → \overrightarrow{\{b, a}, \vec{c}\}, \overrightarrow{\{\boldsymbol{a}, \boldsymbol{c}, \vec{b}\}} { b , a , c } , { a , c , b } { c → , b , a ⃗ } \overrightarrow{\{c}, \boldsymbol{b}, \vec{a}\} { c , b , a }
定义1 设 a , b \boldsymbol{a}, \boldsymbol{b} a , b a \boldsymbol{a} a b \boldsymbol{b} b a × b \boldsymbol{a} \times \boldsymbol{b} a × b a \boldsymbol{a} a b \boldsymbol{b} b a × b \boldsymbol{a} \times \boldsymbol{b} a × b a × b \boldsymbol{a} \times \boldsymbol{b} a × b a , b \boldsymbol{a}, \boldsymbol{b} a , b { a , b , a × b } \{\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{a} \times \boldsymbol{b}\} { a , b , a × b } ∣ a × b ∣ = ∣ a ∣ ∣ b ∣ sin ⟨ a , b ⟩ |\boldsymbol{a} \times \boldsymbol{b}|=|\boldsymbol{a}||\boldsymbol{b}| \sin \langle\boldsymbol{a}, \boldsymbol{b}\rangle ∣ a × b ∣ = ∣ a ∣∣ b ∣ sin ⟨ a , b ⟩
称向量 a × b \boldsymbol{a} \times \boldsymbol{b} a × b a \boldsymbol{a} a b \boldsymbol{b} b
定理1 两不共线向量 a \boldsymbol{a} a b \boldsymbol{b} b ∣ a × b ∣ |\boldsymbol{a} \times \boldsymbol{b}| ∣ a × b ∣ a \boldsymbol{a} a b \boldsymbol{b} b
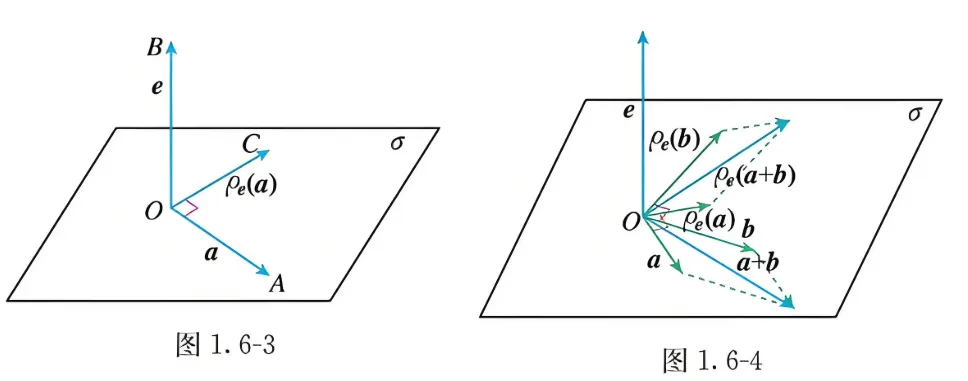
设 e e e a a a e e e O O O O O O e \boldsymbol{e} e O A → = a , O B → = e \overrightarrow{O A}=\boldsymbol{a}, \overrightarrow{O B}=\boldsymbol{e} O A = a , OB = e O O O O A → \overrightarrow{O A} O A 90 ∘ 90^{\circ} 9 0 ∘ e \boldsymbol{e} e a \boldsymbol{a} a b \boldsymbol{b} b
ρ e ( a + b ) = ρ e ( a ) + ρ e ( b ) . \rho_e(\boldsymbol{a}+\boldsymbol{b})=\rho_e(\boldsymbol{a})+\rho_e(\boldsymbol{b}) . ρ e ( a + b ) = ρ e ( a ) + ρ e ( b ) .
命题1 设 e e e a a a
e × a = ρ e ( a e ⊥ ) , e \times a=\rho_e\left(a_e^{\perp}\right), e × a = ρ e ( a e ⊥ ) , 其中 a e ⊥ a_e^{\perp} a e ⊥ a a a e e e a \boldsymbol{a} a e \boldsymbol{e} e e × a = 0 = ρ e ( a e ⊥ ) \boldsymbol{e} \times \boldsymbol{a}=\mathbf{0}=\rho_e\left(\boldsymbol{a}_{\boldsymbol{e}}^{\perp}\right) e × a = 0 = ρ e ( a e ⊥ ) a \boldsymbol{a} a e \boldsymbol{e} e e × a \boldsymbol{e} \times \boldsymbol{a} e × a ρ e ( a e ˙ ) \rho_e(\boldsymbol{a} \dot{e}) ρ e ( a e ˙ ) e \boldsymbol{e} e a \boldsymbol{a} a
∣ e × a ∣ = ∣ a ∣ sin ⟨ a , e ⟩ = ∣ a e ⊥ ∣ = ∣ ρ e ( a e ⊥ ) ∣ , |e \times a|=|a| \sin \langle\boldsymbol{a}, \boldsymbol{e}\rangle=\left|a_e^{\perp}\right|=\left|\rho_e\left(a_e^{\perp}\right)\right|, ∣ e × a ∣ = ∣ a ∣ sin ⟨ a , e ⟩ = a e ⊥ = ρ e ( a e ⊥ ) , 并且 { e , a → , e × a } \overrightarrow{\{e, a}, \boldsymbol{e} \times \boldsymbol{a}\} { e , a , e × a } { e , a → , ρ e ( a e ⊥ ) } \left.\overrightarrow{\{e, a}, \rho_e\left(a_e^{\perp}\right)\right\} { e , a , ρ e ( a e ⊥ ) } ρ e ( a e ⊥ ) \rho_e\left(a_e^{\perp}\right) ρ e ( a e ⊥ ) e × a e \times a e × a e × a = ρ e ( a e ⊥ ) e \times a=\rho_e\left(a_e^{\perp}\right) e × a = ρ e ( a e ⊥ )
命题2 向量的外积满足以下性质:
(1) a × b = − b × a \boldsymbol{a} \times \boldsymbol{b}=-\boldsymbol{b} \times \boldsymbol{a} a × b = − b × a ( λ a ) × b = λ ( a × b ) (\lambda \boldsymbol{a}) \times \boldsymbol{b}=\lambda(\boldsymbol{a} \times \boldsymbol{b}) ( λ a ) × b = λ ( a × b ) ( a + b ) × c = a × c + b × c (\boldsymbol{a}+\boldsymbol{b}) \times \boldsymbol{c}=\boldsymbol{a} \times \boldsymbol{c}+\boldsymbol{b} \times \boldsymbol{c} ( a + b ) × c = a × c + b × c { e 1 , e 2 , e 3 } → \overrightarrow{\left\{e_1, e_2, \boldsymbol{e}_3\right\}} { e 1 , e 2 , e 3 } a \boldsymbol{a} a b \boldsymbol{b} b ( a 1 , a 2 , a 3 ) \left(a_1, a_2, a_3\right) ( a 1 , a 2 , a 3 ) ( b 1 , b 2 , b 3 ) \left(b_1, b_2, b_3\right) ( b 1 , b 2 , b 3 ) a × b \boldsymbol{a} \times \boldsymbol{b} a × b
( a 2 b 3 − a 3 b 2 , a 3 b 1 − a 1 b 3 , a 1 b 2 − a 2 b 1 ) . \left(a_2 b_3-a_3 b_2, a_3 b_1-a_1 b_3, a_1 b_2-a_2 b_1\right) . ( a 2 b 3 − a 3 b 2 , a 3 b 1 − a 1 b 3 , a 1 b 2 − a 2 b 1 ) . e 1 × e 2 = e 3 , e 2 × e 3 = e 1 , e 3 × e 1 = e 2 . \boldsymbol{e}_1 \times \boldsymbol{e}_2=\boldsymbol{e}_3, \boldsymbol{e}_2 \times \boldsymbol{e}_3=e_1, e_3 \times e_1=e_2 . e 1 × e 2 = e 3 , e 2 × e 3 = e 1 , e 3 × e 1 = e 2 . 依题意, 有
a = a 1 e 1 + a 2 e 2 + a 3 e 3 , b = b 1 e 1 + b 2 e 2 + b 3 e 3 , \boldsymbol{a}=a_1 \boldsymbol{e}_1+a_2 \boldsymbol{e}_2+a_3 \boldsymbol{e}_3, \boldsymbol{b}=b_1 \boldsymbol{e}_1+b_2 \boldsymbol{e}_2+b_3 \boldsymbol{e}_3, a = a 1 e 1 + a 2 e 2 + a 3 e 3 , b = b 1 e 1 + b 2 e 2 + b 3 e 3 , 利用命题 2 , 可以得到
a × b = ( a 1 e 1 + a 2 e 2 + a 3 e 3 ) × ( b 1 e 1 + b 2 e 2 + b 3 e 3 ) = a 1 e 1 × ( b 1 e 1 + b 2 e 2 + b 3 e 3 ) + a 2 e 2 × ( b 1 e 1 + b 2 e 2 + b 3 e 3 ) + a 3 e 3 × ( b 1 e 1 + b 2 e 2 + b 3 e 3 ) = a 1 e 1 × b 2 e 2 + a 1 e 1 × b 3 e 3 + a 2 e 2 × b 1 e 1 + a 2 e 2 × b 3 e 3 + a 3 e 3 × b 1 e 1 + a 3 e 3 × b 2 e 2 = a 1 b 2 e 3 − a 1 b 3 e 2 − a 2 b 1 e 3 + a 2 b 3 e 1 + a 3 b 1 e 2 − a 3 b 2 e 1 = ( a 2 b 3 − a 3 b 2 ) e 1 + ( a 3 b 1 − a 1 b 3 ) e 2 + ( a 1 b 2 − a 2 b 1 ) e 3 . \begin{aligned}
\boldsymbol{a} \times \boldsymbol{b} & =\left(a_1 \boldsymbol{e}_1+a_2 \boldsymbol{e}_2+a_3 \boldsymbol{e}_3\right) \times\left(b_1 \boldsymbol{e}_1+b_2 \boldsymbol{e}_2+b_3 \boldsymbol{e}_3\right) \\
& =a_1 \boldsymbol{e}_1 \times\left(b_1 \boldsymbol{e}_1+b_2 \boldsymbol{e}_2+b_3 \boldsymbol{e}_3\right)+a_2 \boldsymbol{e}_2 \times\left(b_1 \boldsymbol{e}_1+b_2 \boldsymbol{e}_2+b_3 \boldsymbol{e}_3\right)+a_3 \boldsymbol{e}_3 \times\left(b_1 \boldsymbol{e}_1+b_2 \boldsymbol{e}_2+b_3 \boldsymbol{e}_3\right) \\
& =a_1 \boldsymbol{e}_1 \times b_2 \boldsymbol{e}_2+a_1 \boldsymbol{e}_1 \times b_3 \boldsymbol{e}_3+a_2 \boldsymbol{e}_2 \times b_1 \boldsymbol{e}_1+a_2 \boldsymbol{e}_2 \times b_3 \boldsymbol{e}_3+a_3 \boldsymbol{e}_3 \times b_1 \boldsymbol{e}_1+a_3 \boldsymbol{e}_3 \times b_2 \boldsymbol{e}_2 \\
& =a_1 b_2 \boldsymbol{e}_3-a_1 b_3 \boldsymbol{e}_2-a_2 b_1 \boldsymbol{e}_3+a_2 b_3 \boldsymbol{e}_1+a_3 b_1 \boldsymbol{e}_2-a_3 b_2 \boldsymbol{e}_1 \\
& =\left(a_2 b_3-a_3 b_2\right) \boldsymbol{e}_1+\left(a_3 b_1-a_1 b_3\right) \boldsymbol{e}_2+\left(a_1 b_2-a_2 b_1\right) \boldsymbol{e}_3 .
\end{aligned} a × b = ( a 1 e 1 + a 2 e 2 + a 3 e 3 ) × ( b 1 e 1 + b 2 e 2 + b 3 e 3 ) = a 1 e 1 × ( b 1 e 1 + b 2 e 2 + b 3 e 3 ) + a 2 e 2 × ( b 1 e 1 + b 2 e 2 + b 3 e 3 ) + a 3 e 3 × ( b 1 e 1 + b 2 e 2 + b 3 e 3 ) = a 1 e 1 × b 2 e 2 + a 1 e 1 × b 3 e 3 + a 2 e 2 × b 1 e 1 + a 2 e 2 × b 3 e 3 + a 3 e 3 × b 1 e 1 + a 3 e 3 × b 2 e 2 = a 1 b 2 e 3 − a 1 b 3 e 2 − a 2 b 1 e 3 + a 2 b 3 e 1 + a 3 b 1 e 2 − a 3 b 2 e 1 = ( a 2 b 3 − a 3 b 2 ) e 1 + ( a 3 b 1 − a 1 b 3 ) e 2 + ( a 1 b 2 − a 2 b 1 ) e 3 . 命题 4 设 a , b a, b a , b c c c
( a × b ) × c = ( a ⋅ c ) b − ( b ⋅ c ) a . (a \times b) \times c=(a \cdot c) b-(b \cdot c) a . ( a × b ) × c = ( a ⋅ c ) b − ( b ⋅ c ) a . 证明: 设 e 1 e_1 e 1 c c c λ \lambda λ c = λ e 1 c=\lambda e_1 c = λ e 1 e 1 e_1 e 1 e 2 e_2 e 2 e 3 = e 1 × e 2 e_3=e_1 \times e_2 e 3 = e 1 × e 2 { e 1 , e 2 , e 3 } → \overrightarrow{\left\{e_1, e_2, e_3\right\}} { e 1 , e 2 , e 3 } a = a 1 e 1 + a 2 e 2 + a 3 e 3 , b = b 1 e 1 + b 2 e 2 + b 3 e 3 \boldsymbol{a}=a_1 \boldsymbol{e}_1+a_2 \boldsymbol{e}_2+a_3 \boldsymbol{e}_3, \boldsymbol{b}=b_1 \boldsymbol{e}_1+b_2 \boldsymbol{e}_2+b_3 \boldsymbol{e}_3 a = a 1 e 1 + a 2 e 2 + a 3 e 3 , b = b 1 e 1 + b 2 e 2 + b 3 e 3
( a × b ) × e 1 = ( a 1 b 2 − a 2 b 1 ) e 2 − ( a 3 b 1 − a 1 b 3 ) e 3 . (\boldsymbol{a} \times \boldsymbol{b}) \times \boldsymbol{e}_1=\left(a_1 b_2-a_2 b_1\right) \boldsymbol{e}_2-\left(a_3 b_1-a_1 b_3\right) \boldsymbol{e}_3 . ( a × b ) × e 1 = ( a 1 b 2 − a 2 b 1 ) e 2 − ( a 3 b 1 − a 1 b 3 ) e 3 . 通过直接计算, 可以得到
( a ⋅ e 1 ) b − ( b ⋅ e 1 ) a = ( a 1 b 2 − a 2 b 1 ) e 2 − ( a 3 b 1 − a 1 b 3 ) e 3 . \left(\boldsymbol{a} \cdot \boldsymbol{e}_1\right) \boldsymbol{b}-\left(\boldsymbol{b} \cdot \boldsymbol{e}_1\right) \boldsymbol{a}=\left(a_1 b_2-a_2 b_1\right) \boldsymbol{e}_2-\left(a_3 b_1-a_1 b_3\right) \boldsymbol{e}_3 . ( a ⋅ e 1 ) b − ( b ⋅ e 1 ) a = ( a 1 b 2 − a 2 b 1 ) e 2 − ( a 3 b 1 − a 1 b 3 ) e 3 . 所以
( a ⋅ e 1 ) b − ( b ⋅ e 1 ) a = ( a × b ) × e 1 . \left(a \cdot e_1\right) b-\left(b \cdot e_1\right) a=(a \times b) \times e_1 . ( a ⋅ e 1 ) b − ( b ⋅ e 1 ) a = ( a × b ) × e 1 . 在上式两边乘 λ \lambda λ
{width=400px}
{width=300px}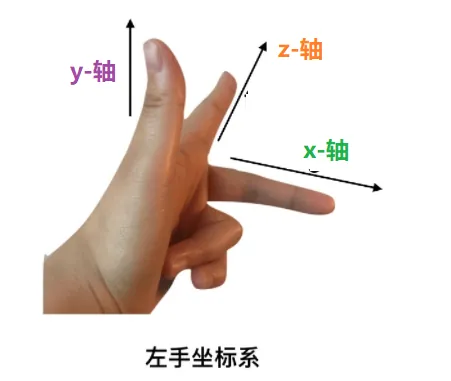
{width=300px}
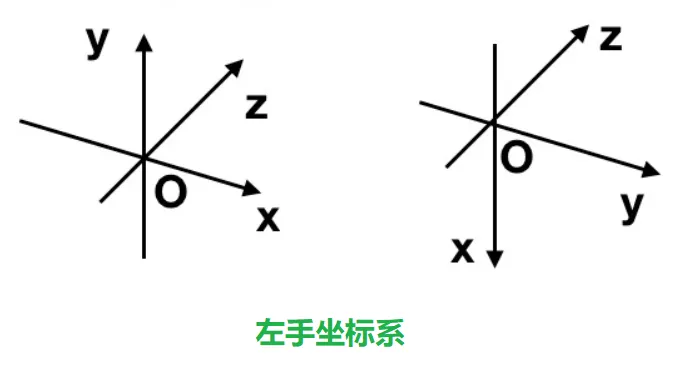{width=400px}
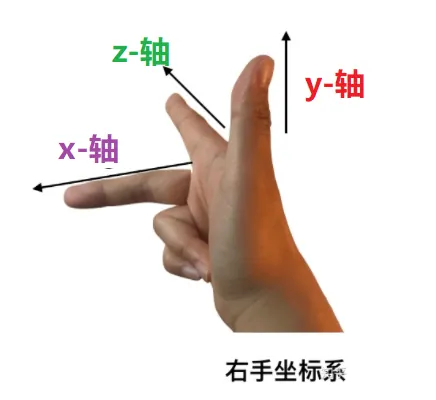{width=300px}
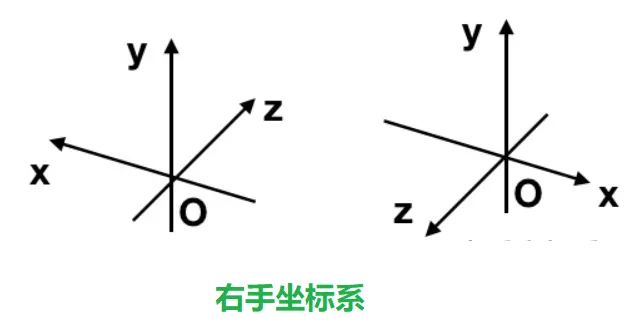{width=400px}
