线性变换的意义 在大多数的教科书中, 线性映射和线性变换被区别为两个概念。如果映射是发生在一个集合上的同一个坐标系中, 线性映射就被称为线性变换。线性变换作为线性映射的特例, 就是把集合上的两个坐标系合并为一个。
简单理解:二维到二维是变换,比如平面图形的旋转变换。 三维到二维是映射,比如灯光照射在球体上,墙面上留下球的影子,这就把三维球体映射成了二维平面。
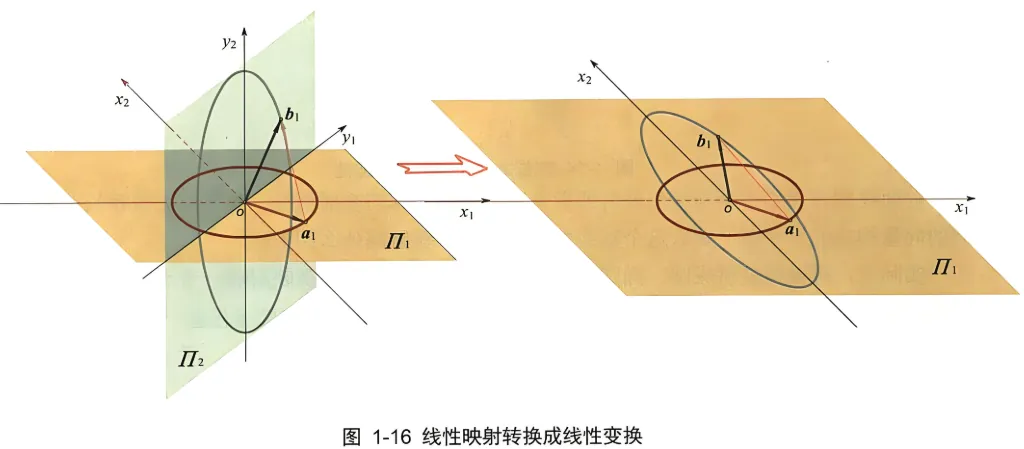
例如把二维平面圆的映射整合成变换如图 1-16 所示, 以原点为不变轴心, 把 Π 2 \Pi_2 Π 2 y 1 y_1 y 1 x 1 x_1 x 1 y 2 y_2 y 2 x 2 x_2 x 2
整合后的图形用平面直角坐标系表示就是图 1-17。
直角坐标系下的图形清楚地显示了一个圆被线性变换为一个椭圆。相应地,圆上的一个向量 a 1 \boldsymbol{a}_1 a 1 b 1 \boldsymbol{b}_1 b 1
例子 在线性代数中, 我们主要讨论的是由矩阵所决定的线性变换的各种特性。下面看两个具体的线性变换的例子 (下面的 “'”为线性变换 T ( T( T ( a 1 + a 2 ( = a 3 ) \boldsymbol{a}_1+\boldsymbol{a}_2\left(=\boldsymbol{a}_3\right) a 1 + a 2 ( = a 3 ) a 3 ′ \boldsymbol{a}_3{ }^{\prime} a 3 ′ a 1 \boldsymbol{a}_1 a 1 a 2 \boldsymbol{a}_2 a 2 a 1 ′ \boldsymbol{a}_1{ }^{\prime} a 1 ′ a 2 ′ \boldsymbol{a}_2{ }^{\prime} a 2 ′ a 1 ′ + a 2 ′ \boldsymbol{a}_1{ }^{\prime}+\boldsymbol{a}_2{ }^{\prime} a 1 ′ + a 2 ′ k k k a 1 \boldsymbol{a}_1 a 1 k a 1 k \boldsymbol{a}_1 k a 1 ( k a 1 ) ′ \left(k \boldsymbol{a}_1\right)^{\prime} ( k a 1 ) ′ k k k a 1 \boldsymbol{a}_1 a 1 a 1 ′ \boldsymbol{a}_1{ }^{\prime} a 1 ′ k a 1 ′ k \boldsymbol{a}_1{ }^{\prime} k a 1 ′
( a 1 + a 2 ) ′ = a 1 ′ + a 2 ′ , ( k a 1 ) ′ = k a 1 ′ 。 \begin{gathered}
\left(a_1+a_2\right)^{\prime}=a_1{ }^{\prime}+a_2{ }^{\prime}, \\
\left(k a_1\right)^{\prime}=k a_1{ }^{\prime} 。
\end{gathered} ( a 1 + a 2 ) ′ = a 1 ′ + a 2 ′ , ( k a 1 ) ′ = k a 1 ′ 。
另一个例子 (见图 1-19): 在建立了空间笛卡尔直角坐标系的三维向量空间中, 把每一个向量投影在坐标面 x o y x o y x oy a = ( a , b , c ) \boldsymbol{a}=(a, b, c) a = ( a , b , c ) a ′ = ( a , b , 0 ) \boldsymbol{a}^{\prime}=(a, b, 0) a ′ = ( a , b , 0 )
( a 1 + a 2 ) ′ = a 1 ′ + a 2 ′ \left(\boldsymbol{a}_1+\boldsymbol{a}_2\right)^{\prime}=\boldsymbol{a}_1{ }^{\prime}+\boldsymbol{a}_2{ }^{\prime} ( a 1 + a 2 ) ′ = a 1 ′ + a 2 ′
( k a ) ′ = k a ′ (k \boldsymbol{a})^{\prime}=k \boldsymbol{a}^{\prime} ( k a ) ′ = k a ′
这两个变换有一个共同的性质: 两个向量之和变换后, 所得的向量恰好是把这两个向量变换后所得向量之和; 数 k k k k k k F F F V V V T T T
T ( a + b ) = T a + T b ( a , b ∈ V ) T ( k a ) = k T a ( k ∈ F , a ∈ V ) \begin{aligned}
& T(\boldsymbol{a}+\boldsymbol{b})=T \boldsymbol{a}+T \boldsymbol{b} \quad(\boldsymbol{a}, \boldsymbol{b} \in V) \\
& T(k \boldsymbol{a})=k T \boldsymbol{a} \quad(k \in F, \boldsymbol{a} \in V)
\end{aligned} T ( a + b ) = T a + T b ( a , b ∈ V ) T ( k a ) = k T a ( k ∈ F , a ∈ V ) 则称 T T T V V V
下面介绍2个常见的映射。
变换的矩阵表示 上面描述了线性变换,那么如何表示这种变换呢?答案就是:矩阵。下面给出2个常用的二维变换矩阵:缩放矩阵和旋转矩阵
缩放矩阵 缩放变换中,如果一个图片以原点 ( 0 , 0 ) (0,0) ( 0 , 0 ) s s s ( x , y ) (x, y) ( x , y )
x ′ = s x y ′ = s y \begin{aligned}
& x^{\prime}=s x \\
& y^{\prime}=s y
\end{aligned} x ′ = s x y ′ = sy 写成矩阵形式为:
[ x ′ y ′ ] = [ s x 0 0 s y ] [ x y ] \left[\begin{array}{l}
x^{\prime} \\
y^{\prime}
\end{array}\right]=\left[\begin{array}{ll}
s_x & 0 \\
0 & s_y
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right] [ x ′ y ′ ] = [ s x 0 0 s y ] [ x y ] 当然,我们也可以给 x 轴和 y 轴不同的缩放倍数 s x s x s x s y s y sy
[ x ′ y ′ ] = [ s x 0 0 s y ] [ x y ] . . . ( 图像缩放公式 ) \boxed{
\left[\begin{array}{l}
x^{\prime} \\
y^{\prime}
\end{array}\right]=\left[\begin{array}{cc}
s_x & 0 \\
0 & s_y
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right] ...(\text{图像缩放公式})
} [ x ′ y ′ ] = [ s x 0 0 s y ] [ x y ] ... ( 图像缩放公式 ) 下图展示了图像缩放示意图
通过观察可以看到,缩放矩阵,只有主对角线有元素,其它元素为0
图像旋转矩阵 我们默认旋转变换(Rotate)都绕着原点( 0 , 0 ) (0, 0) ( 0 , 0 ) ( x , y ) (x,y) ( x , y ) ( 0 , 0 ) (0,0) ( 0 , 0 ) θ \theta θ
[ x ′ y ′ ] = [ cos θ − sin θ sin θ cos θ ] [ x y ] . . . ( 图像旋转公式 ) \boxed
{
\left[\begin{array}{l}
x^{\prime} \\
y^{\prime}
\end{array}\right]=\left[\begin{array}{cc}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right] ...(\text{图像旋转公式})
} [ x ′ y ′ ] = [ cos θ sin θ − sin θ cos θ ] [ x y ] ... ( 图像旋转公式 ) 证明
我们在直角坐标系中绘制一个边长为 1 的正方形,点 A A A ( 1 , 0 ) (1,0) ( 1 , 0 ) B B B ( 0 , 1 ) (0,1) ( 0 , 1 ) ( 0 , 0 ) (0,0) ( 0 , 0 ) θ \theta θ
我们设原坐标里任一点( x , y ) (x,y) ( x , y ) ( x ′ , y ′ ) (x',y') ( x ′ , y ′ )
[ x ′ y ′ ] = [ A B C D ] [ x y ] \left[\begin{array}{l}
x^{\prime} \\
y^{\prime}
\end{array}\right]=\left[\begin{array}{ll}
A & B \\
C & D
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right] [ x ′ y ′ ] = [ A C B D ] [ x y ] 接下来去两个特殊点,代入点 A A A ( 1 , 0 ) (1,0) ( 1 , 0 )
[ cos θ sin θ ] = [ A B C D ] [ 1 0 ] \left[\begin{array}{c}
\cos \theta \\
\sin \theta
\end{array}\right]=\left[\begin{array}{ll}
A & B \\
C & D
\end{array}\right]\left[\begin{array}{l}
1 \\
0
\end{array}\right] [ cos θ sin θ ] = [ A C B D ] [ 1 0 ] 解方程得到:
A = cos θ C = sin θ \begin{aligned}
& A=\cos \theta \\
& C=\sin \theta
\end{aligned} A = cos θ C = sin θ 代人点 B B B ( 0 , 1 ) (0,1) ( 0 , 1 )
[ − sin θ cos θ ] = [ A B C D ] [ 0 1 ] \left[\begin{array}{c}
-\sin \theta \\
\cos \theta
\end{array}\right]=\left[\begin{array}{ll}
A & B \\
C & D
\end{array}\right]\left[\begin{array}{l}
0 \\
1
\end{array}\right] [ − sin θ cos θ ] = [ A C B D ] [ 0 1 ] 解方程得到:
B = − sin θ D = cos θ \begin{array}{r}B=-\sin \theta \\ D=\cos \theta \end{array} B = − sin θ D = cos θ 因此,坐标旋转公式为
A rotate = [ cos θ − sin θ sin θ cos θ ] A_{\text {rotate }}=\left[\begin{array}{cc}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{array}\right] A rotate = [ cos θ sin θ − sin θ cos θ ] 下图显示了一个图形旋转。
特别的,如果 θ = 45 ∘ \theta=45^{\circ} θ = 4 5 ∘
A = [ 2 2 − 2 2 2 2 2 2 ] \boldsymbol{A}=\left[\begin{array}{cc}
\frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \\
\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}
\end{array}\right] A = [ 2 2 2 2 − 2 2 2 2 ] 这意味着任何一个向量乘以该矩阵将旋转45 ∘ 45^{\circ} 4 5 ∘
更多变换矩阵的介绍请点击 矩阵变换
 {width=600px}
{width=600px}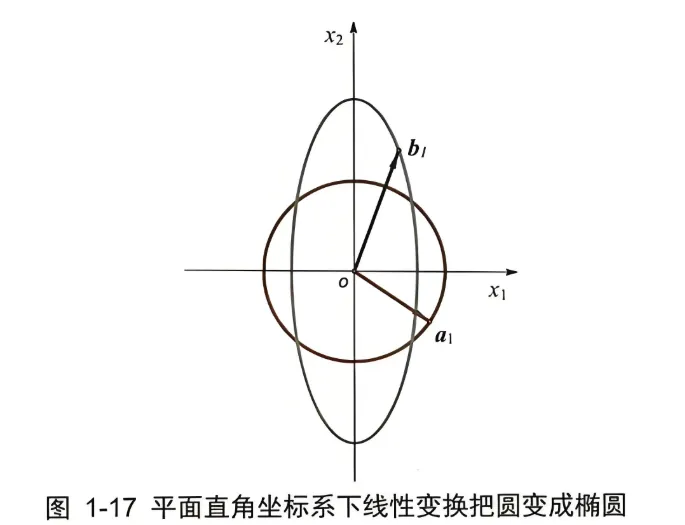 {width=500px}
{width=500px}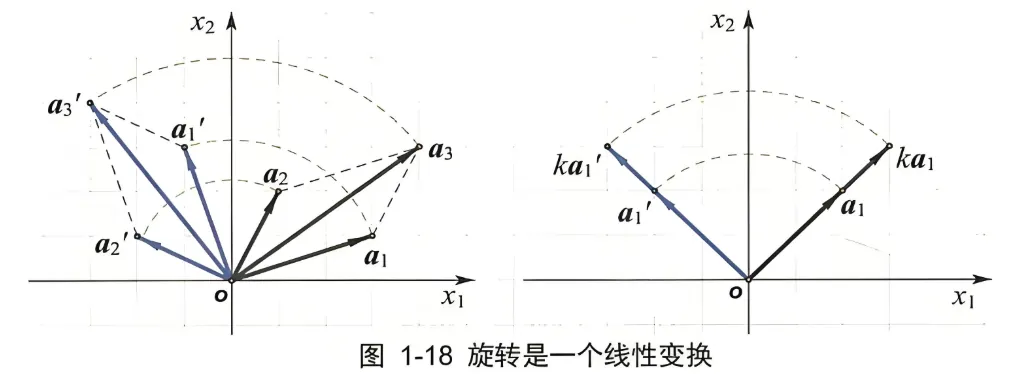 {width=600px}
{width=600px}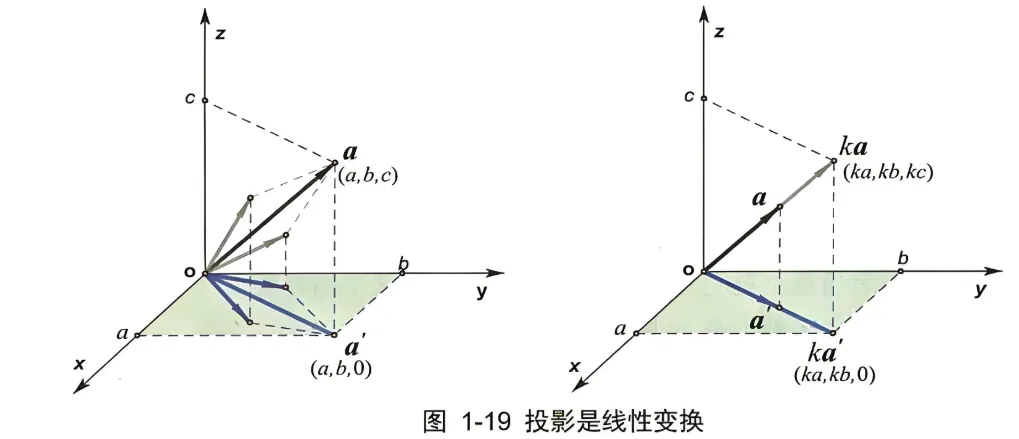 {width=600px}
{width=600px}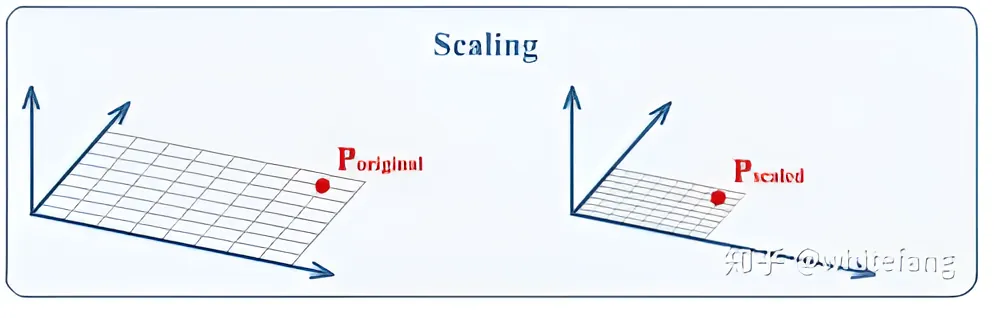 {width=600px}
{width=600px}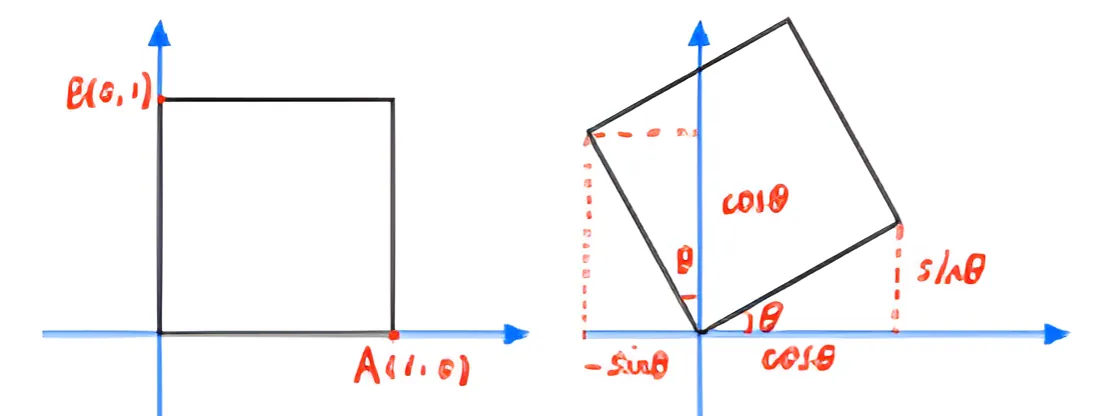 {width=500px}
{width=500px}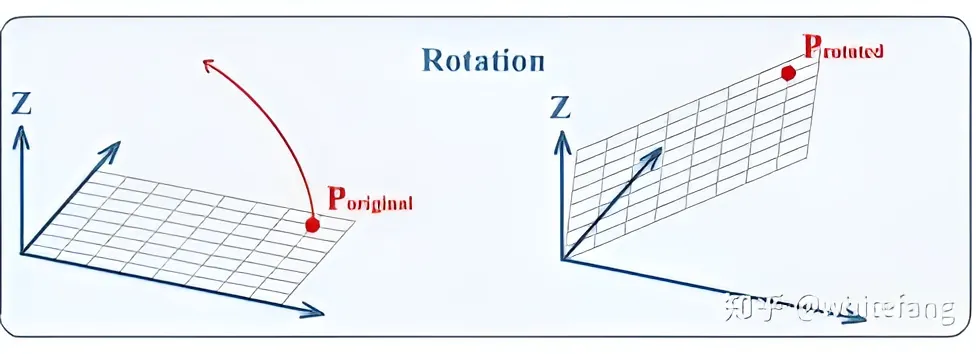 {width=600px}
{width=600px}