说明:我们把单位行矩阵看成向量α \alpha α β \beta β
矩阵乘法包括8个视角:
向量 x 向量 (2个视角,分为左乘和右乘)
矩阵 x 向量 (2个视角,分为左乘和右乘)
矩阵 x 矩阵 (4个视角,分为左乘和右乘)
本文节选自《the-Art-of-Linear-Algebra-zh-CN.pdf》,原文给出了8个视角的解释,因为8个视角太多了,最常用的是下面3个混合模式。所以本站先给出3个常用的混合模式,再列出原书给出的8个模式
本节内容是高度抽象甚至贯穿《线性代数》全书,因此初学者不要期望一下子就掌握。
矩阵的四个视角 设有一个矩阵A A A
A = [ 1 4 2 5 3 6 ] A=\left[\begin{array}{ll}
1 & 4 \\
2 & 5 \\
3 & 6
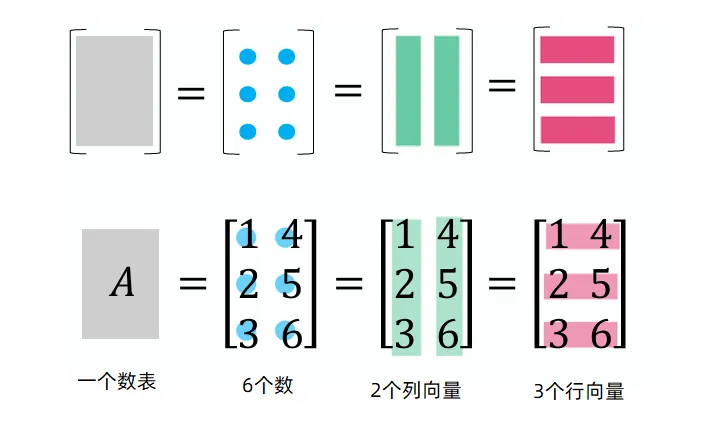
\end{array}\right] A = 1 2 3 4 5 6 第一个视角:就是一个数表。
第二个视角:就是6个数,排成了2行3列
第三个视角:两个列向量(最常用)
第四个视角:三个行向量。
一个矩阵 ( m × n ) (m \times n) ( m × n ) m n m n mn n n n m m m
以下表述里,默认都是使用列向量α \alpha α α ∗ \alpha^* α ∗ α T \alpha^T α T
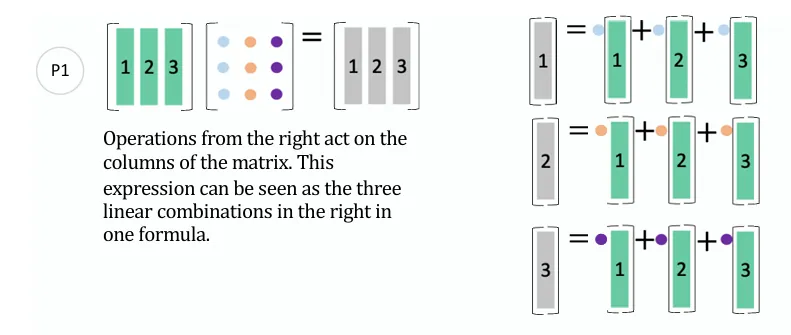
矩阵乘法的几个常用的重要视角 列模式 参考下图,数字矩阵 乘以颜色矩阵 的结果相当于颜色矩阵对数字列做线性组合。
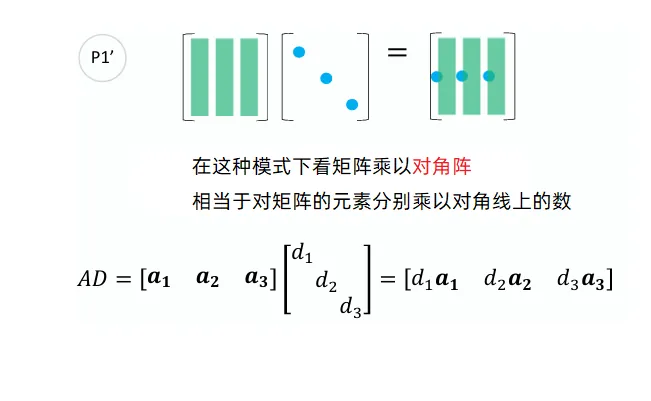
特别的,如果颜色矩阵是对角形矩阵,那么结果就相当于对对角线矩阵的数字直接作用到前面矩阵的每一列上。
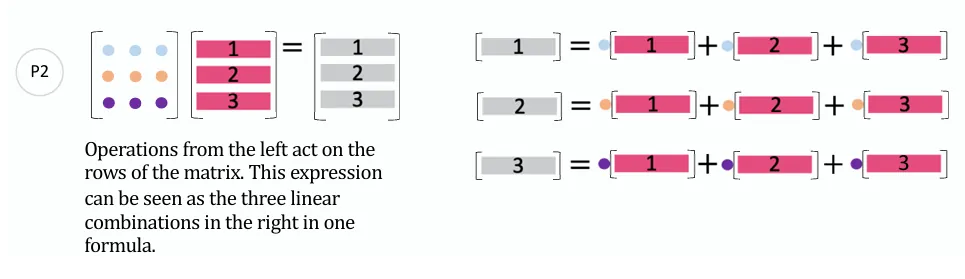
行模式 参考下图,颜色矩阵 乘以数字矩阵 的结果相当于颜色矩阵按行对数字矩阵做线性组合。
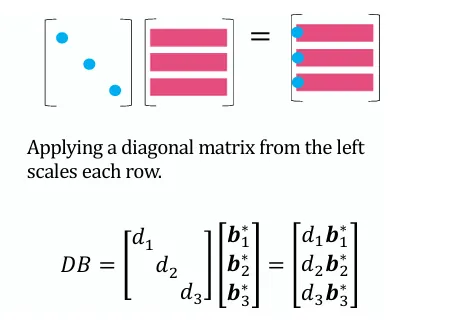
下图显示对角形矩阵作用的结果。(我们默认b b b b ∗ b^* b ∗
混合模式 如果将上面的乘法组合在一起就是
下面列出《the-Art-of-Linear-Algebra-zh-CN.pdf》所有的视角,
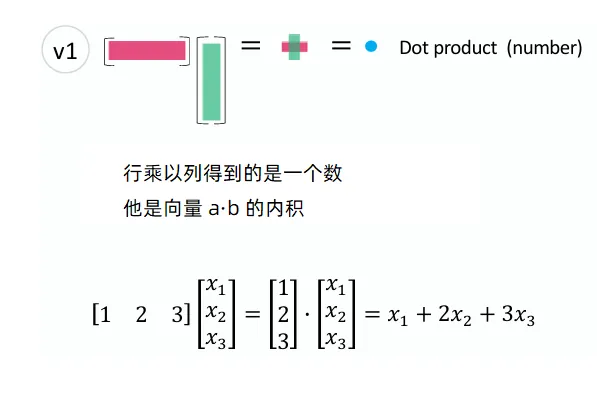
向量与向量相乘的两个视角 向量与向量相乘,一般会涉及两种形式:一种是行向量乘以列向量,其结果为一个数值(标量),也称为内积 ;另一种是列向量乘以行向量,其结果为秩为 1 的矩阵,也称为外积 。
假设 n n n a = [ a 1 a 2 ⋮ a n ] , b = [ b 1 b 2 ⋮ b n ] a =\left[\begin{array}{c}a_1 \\ a_2 \\ \vdots \\ a_n\end{array}\right], b =\left[\begin{array}{c}b_1 \\ b_2 \\ \vdots \\ b_n\end{array}\right] a = a 1 a 2 ⋮ a n , b = b 1 b 2 ⋮ b n a T = [ a 1 a 2 … a n ] , b T = [ b 1 b 2 … b n ] a ^{ T }=\left[\begin{array}{llll}a_1 & a_2 & \ldots & a_n\end{array}\right], b ^{ T }=\left[\begin{array}{llll}b_1 & b_2 & \ldots & b_n\end{array}\right] a T = [ a 1 a 2 … a n ] , b T = [ b 1 b 2 … b n ]
行乘以列 行向量乘以列向量(内积)---结果是一个数值
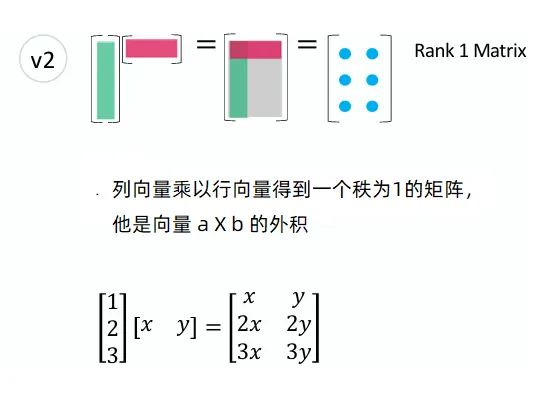
列乘以行(主流视角) 列向量乘以行向量(外积)---结果是一个矩阵
结论
行向量乘以列向量(内积): a T b = a 1 b 1 + a 2 b 2 + ⋯ + a n b n a ^{ T } b =a_1 b_1+a_2 b_2+\cdots+a_n b_n a T b = a 1 b 1 + a 2 b 2 + ⋯ + a n b n
列向量乘以行向量(外积):
a b T = [ a 1 a 2 ⋮ a n ] [ b 1 b 2 … b n ] = [ a 1 b 1 a 1 b 2 … a 1 b n a 2 b 1 a 2 b 2 … a 2 b n ⋮ ⋮ ⋱ ⋮ a n b 1 a n b 2 … a n b n ] a b ^{T}=\left[\begin{array}{c}
a_1 \\
a_2 \\
\vdots \\
a_n
\end{array}\right]\left[\begin{array}{llll}
b_1 & b_2 & \ldots & b_n
\end{array}\right]=\left[\begin{array}{cccc}
a_1 b_1 & a_1 b_2 & \ldots & a_1 b_n \\
a_2 b_1 & a_2 b_2 & \ldots & a_2 b_n \\
\vdots & \vdots & \ddots & \vdots \\
a_n b_1 & a_n b_2 & \ldots & a_n b_n
\end{array}\right] a b T = a 1 a 2 ⋮ a n [ b 1 b 2 … b n ] = a 1 b 1 a 2 b 1 ⋮ a n b 1 a 1 b 2 a 2 b 2 ⋮ a n b 2 … … ⋱ … a 1 b n a 2 b n ⋮ a n b n 举例说明:
假设列向量 a = [ 1 0 2 ] , b = [ 1 2 3 ] ,则: a T b = [ 1 0 2 ] [ 1 2 3 ] = 1 × 1 + 0 × 2 + 2 × 3 = 7 a b T = [ 1 0 2 ] [ 1 2 3 ] = [ 1 2 3 0 0 0 2 4 6 ] \begin{aligned}
&\text { 假设列向量 } a =\left[\begin{array}{l}
1 \\
0 \\
2
\end{array}\right], b =\left[\begin{array}{l}
1 \\
2 \\
3
\end{array}\right] \text { ,则:}\\
&\begin{aligned}
& a ^{T} b =\left[\begin{array}{lll}
1 & 0 & 2
\end{array}\right]\left[\begin{array}{l}
1 \\
2 \\
3
\end{array}\right]=1 \times 1+0 \times 2+2 \times 3=7 \\
& a b ^{T}=\left[\begin{array}{l}
1 \\
0 \\
2
\end{array}\right]\left[\begin{array}{lll}
1 & 2 & 3
\end{array}\right]=\left[\begin{array}{lll}
1 & 2 & 3 \\
0 & 0 & 0 \\
2 & 4 & 6
\end{array}\right]
\end{aligned}
\end{aligned} 假设列向量 a = 1 0 2 , b = 1 2 3 ,则: a T b = [ 1 0 2 ] 1 2 3 = 1 × 1 + 0 × 2 + 2 × 3 = 7 a b T = 1 0 2 [ 1 2 3 ] = 1 0 2 2 0 4 3 0 6 矩阵与向量(向量与矩阵)相乘的2个视角 设矩阵 A = [ a 11 a 12 … a 1 n a 21 a 22 … a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 … a m n ] ∈ R m × n , n A=\left[\begin{array}{cccc}a_{11} & a_{12} & \ldots & a_{1 n} \\ a_{21} & a_{22} & \ldots & a_{2 n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m 1} & a_{m 2} & \ldots & a_{m n}\end{array}\right] \in R ^{m \times n}, ~ n A = a 11 a 21 ⋮ a m 1 a 12 a 22 ⋮ a m 2 … … ⋱ … a 1 n a 2 n ⋮ a mn ∈ R m × n , n x = [ x 1 x 2 ⋮ x n ] x =\left[\begin{array}{c}x_1 \\ x_2 \\ \vdots \\ x_n\end{array}\right] x = x 1 x 2 ⋮ x n A x A x A x
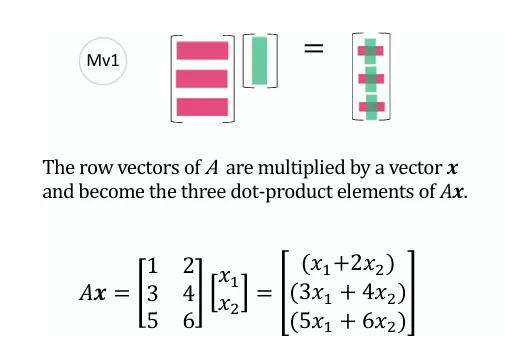
行视角 矩阵乘法视角:根据矩阵乘法规则,计算其结果:
A x = [ a 11 a 12 … a 1 n a 21 a 22 … a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 … a m n ] [ x 1 x 2 ⋮ x n ] = [ a 11 x 1 + a 22 x 2 + ⋯ + a n n x n a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n ⋮ a m 1 x 1 + a m 2 x 2 + ⋯ + a m n x n ] A x =\left[\begin{array}{cccc}
a_{11} & a_{12} & \ldots & a_{1 n} \\
a_{21} & a_{22} & \ldots & a_{2 n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m 1} & a_{m 2} & \ldots & a_{m n}
\end{array}\right]\left[\begin{array}{c}
x_1 \\
x_2 \\
\vdots \\
x_n
\end{array}\right]=\left[\begin{array}{c}
a_{11} x_1+a_{22} x_2+\cdots+a_{n n} x_n \\
a_{21} x_1+a_{22} x_2+\cdots+a_{2 n} x_n \\
\vdots \\
a_{m 1} x_1+a_{m 2} x_2+\cdots+a_{m n} x_n
\end{array}\right] A x = a 11 a 21 ⋮ a m 1 a 12 a 22 ⋮ a m 2 … … ⋱ … a 1 n a 2 n ⋮ a mn x 1 x 2 ⋮ x n = a 11 x 1 + a 22 x 2 + ⋯ + a nn x n a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n ⋮ a m 1 x 1 + a m 2 x 2 + ⋯ + a mn x n
一般线性方程组 { a 11 x 1 + a 22 x 2 + ⋯ + a n n x n = b 1 a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n = b 2 ⋮ a m 1 x 1 + a m 2 x 2 + ⋯ + a m n x n = b m \left\{\begin{array}{l}a_{11} x_1+a_{22} x_2+\cdots+a_{n n} x_n=b_1 \\ a_{21} x_1+a_{22} x_2+\cdots+a_{2 n} x_n=b_2 \\ \vdots \\ a_{m 1} x_1+a_{m 2} x_2+\cdots+a_{m n} x_n=b_m\end{array}\right. ⎩ ⎨ ⎧ a 11 x 1 + a 22 x 2 + ⋯ + a nn x n = b 1 a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n = b 2 ⋮ a m 1 x 1 + a m 2 x 2 + ⋯ + a mn x n = b m A x = b A x = b A x = b b b b m m m
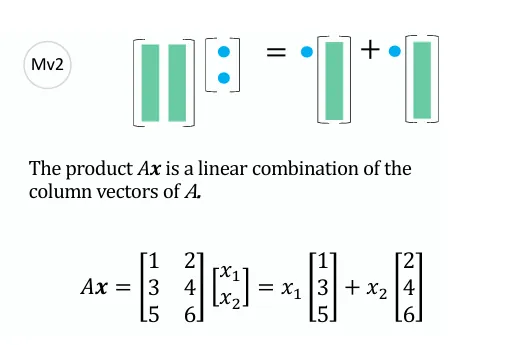
列视角 列向量线性组合视角:将矩阵 A A A n n n m m m
A = [ a 1 a 2 ⋯ a n ] , 其中, m 维列向量 a j = [ a 1 j a 2 j ⋮ a m j ] ( j = 1 , 2 , ⋯ , n ) , A=\left[\begin{array}{llll}
\boldsymbol{a _1 } & \boldsymbol{a _2} & \cdots & \boldsymbol{a _n}
\end{array}\right] \text {, 其中, } m \text { 维列向量 } \boldsymbol{a _j}=\left[\begin{array}{c}
a_{1 j} \\
a_{2 j} \\
\vdots \\
a_{m j}
\end{array}\right](j=1,2, \cdots, n) \text {, } A = [ a 1 a 2 ⋯ a n ] , 其中 , m 维列向量 a j = a 1 j a 2 j ⋮ a mj ( j = 1 , 2 , ⋯ , n ) , 则
A x = [ a 1 a 2 ⋯ a n ] [ x 1 x 2 ⋮ x n ] = x 1 a 1 + x 2 a 2 + ⋯ + x n a n \boldsymbol{A} \boldsymbol{x} =\left[\begin{array}{llll}
\boldsymbol{a _1} & \boldsymbol{a _2} & \cdots & \boldsymbol{a _n}
\end{array}\right]\left[\begin{array}{c}
x_1 \\
x_2 \\
\vdots \\
x_n
\end{array}\right]=x_1 \boldsymbol{a _1}+x_2 \boldsymbol{a _2} +\cdots+x_n \boldsymbol{a _n} A x = [ a 1 a 2 ⋯ a n ] x 1 x 2 ⋮ x n = x 1 a 1 + x 2 a 2 + ⋯ + x n a n 这也就是意味着 A x A x A x A A A A A A x x x
一般线性方程组 { a 11 x 1 + a 22 x 2 + ⋯ + a n n x n = b 1 a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n = b 2 ⋮ a m 1 x 1 + a m 2 x 2 + ⋯ + a m n x n = b m \left\{\begin{array}{l}a_{11} x_1+a_{22} x_2+\cdots+a_{n n} x_n=b_1 \\ a_{21} x_1+a_{22} x_2+\cdots+a_{2 n} x_n=b_2 \\ \vdots \\ a_{m 1} x_1+a_{m 2} x_2+\cdots+a_{m n} x_n=b_m\end{array}\right. ⎩ ⎨ ⎧ a 11 x 1 + a 22 x 2 + ⋯ + a nn x n = b 1 a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n = b 2 ⋮ a m 1 x 1 + a m 2 x 2 + ⋯ + a mn x n = b m
x 1 [ a 11 a 21 ⋮ a m 1 ] + x 2 [ a 12 a 22 ⋮ a m 2 ] + ⋯ + x n [ a 1 n a 2 n ⋮ a m n ] = [ b 1 b 2 ⋮ b m ] x_1\left[\begin{array}{c}
a_{11} \\
a_{21} \\
\vdots \\
a_{m 1}
\end{array}\right]+x_2\left[\begin{array}{c}
a_{12} \\
a_{22} \\
\vdots \\
a_{m 2}
\end{array}\right]+\cdots+x_n\left[\begin{array}{c}
a_{1 n} \\
a_{2 n} \\
\vdots \\
a_{m n}
\end{array}\right]= \left[\begin{array}{c}
b_{1} \\
b_{2} \\
\vdots \\
b_{m}
\end{array}\right] x 1 a 11 a 21 ⋮ a m 1 + x 2 a 12 a 22 ⋮ a m 2 + ⋯ + x n a 1 n a 2 n ⋮ a mn = b 1 b 2 ⋮ b m
例如:A = [ 1 2 3 4 5 6 ] , x = [ x 1 x 2 x 3 ] A=\left[\begin{array}{lll}1 & 2 & 3 \\ 4 & 5 & 6\end{array}\right], ~ x =\left[\begin{array}{l}x_1 \\ x_2 \\ x_3\end{array}\right] A = [ 1 4 2 5 3 6 ] , x = x 1 x 2 x 3
矩阵乘法视角:A x = [ 1 2 3 4 5 6 ] [ x 1 x 2 x 3 ] = [ 1 ⋅ x 1 + 2 ⋅ x 2 + 3 ⋅ x 3 4 ⋅ x 1 + 5 ⋅ x 2 + 6 ⋅ x 3 ] A x =\left[\begin{array}{lll}1 & 2 & 3 \\ 4 & 5 & 6\end{array}\right]\left[\begin{array}{l}x_1 \\ x_2 \\ x_3\end{array}\right]=\left[\begin{array}{l}1 \cdot x_1+2 \cdot x_2+3 \cdot x_3 \\ 4 \cdot x_1+5 \cdot x_2+6 \cdot x_3\end{array}\right] A x = [ 1 4 2 5 3 6 ] x 1 x 2 x 3 = [ 1 ⋅ x 1 + 2 ⋅ x 2 + 3 ⋅ x 3 4 ⋅ x 1 + 5 ⋅ x 2 + 6 ⋅ x 3 ] A x = [ 1 2 3 4 5 6 ] [ x 1 x 2 x 3 ] = x 1 [ 1 4 ] + x 2 [ 2 5 ] + x 3 [ 3 6 ] A x =\left[\begin{array}{lll}1 & 2 & 3 \\ 4 & 5 & 6\end{array}\right]\left[\begin{array}{l}x_1 \\ x_2 \\ x_3\end{array}\right]=x_1\left[\begin{array}{l}1 \\ 4\end{array}\right]+x_2\left[\begin{array}{l}2 \\ 5\end{array}\right]+x_3\left[\begin{array}{l}3 \\ 6\end{array}\right] A x = [ 1 4 2 5 3 6 ] x 1 x 2 x 3 = x 1 [ 1 4 ] + x 2 [ 2 5 ] + x 3 [ 3 6 ]
向量 × \times × 此种形式,一般为一个行向量 b T = [ b 1 b 2 ⋯ b m ] b ^{ T }=\left[\begin{array}{llll}b_1 & b_2 & \cdots & b_m\end{array}\right] b T = [ b 1 b 2 ⋯ b m ] m m m n n n A A A (1)矩阵乘法视角 :
b T A = [ b 1 b 2 ⋯ b m ] [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 ⋯ a m n ] = [ b 1 a 11 + b 2 a 21 + ⋯ + b m a m 1 , b 1 a 12 + b 2 a 22 + ⋯ + b m a m 2 , ⋯ , b 1 a 1 n + b 2 a 2 n + ⋯ + b m a m n ] \begin{aligned}
& b ^{T} A=\left[\begin{array}{llll}
b_1 & b_2 & \cdots & b_m
\end{array}\right]\left[\begin{array}{cccc}
a_{11} & a_{12} & \cdots & a_{1 n} \\
a_{21} & a_{22} & \cdots & a_{2 n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m 1} & a_{m 2} & \cdots & a_{m n}
\end{array}\right] \\
& =\left[\begin{array}{lll}
b_1 a_{11}+b_2 a_{21}+\cdots+b_m a_{m 1}, & b_1 a_{12}+b_2 a_{22}+\cdots+b_m a_{m 2}, & \cdots,
\end{array} b_1 a_{1 n}+b_2 a_{2 n}+\cdots+b_m a_{m n}\right]
\end{aligned} b T A = [ b 1 b 2 ⋯ b m ] a 11 a 21 ⋮ a m 1 a 12 a 22 ⋮ a m 2 ⋯ ⋯ ⋱ ⋯ a 1 n a 2 n ⋮ a mn = [ b 1 a 11 + b 2 a 21 + ⋯ + b m a m 1 , b 1 a 12 + b 2 a 22 + ⋯ + b m a m 2 , ⋯ , b 1 a 1 n + b 2 a 2 n + ⋯ + b m a mn ]
(2)行向量线性组合视角 :此时,将矩阵 A A A m m m n n n A = [ a 1 T a 2 T ⋮ a m T ] A=\left[\begin{array}{c} a _1^{ T } \\ a _2^{ T } \\ \vdots \\ a _m^{ T }\end{array}\right] A = a 1 T a 2 T ⋮ a m T
此处 a i = [ a i 1 a i 2 ⋮ a i n ] ( i = 1 , 2 , ⋯ , m ) a _i=\left[\begin{array}{c}a_{i 1} \\ a_{i 2} \\ \vdots \\ a_{i n}\end{array}\right](i=1,2, \cdots, m) a i = a i 1 a i 2 ⋮ a in ( i = 1 , 2 , ⋯ , m )
b T A = [ b 1 b 2 ⋯ b m ] [ a 1 T a 2 T ⋮ a m T ] = b 1 a 1 T + b 2 a 2 T + ⋯ + b m a m T b ^{T} A=\left[\begin{array}{llll}
b_1 & b_2 & \cdots & b_m
\end{array}\right]\left[\begin{array}{c}
a _1^{T} \\
a _2^{T} \\
\vdots \\
a _m^{T}
\end{array}\right]=b_1 a _1^{T}+b_2 a _2^{T}+\cdots+b_m a _m^{T} b T A = [ b 1 b 2 ⋯ b m ] a 1 T a 2 T ⋮ a m T = b 1 a 1 T + b 2 a 2 T + ⋯ + b m a m T
举例
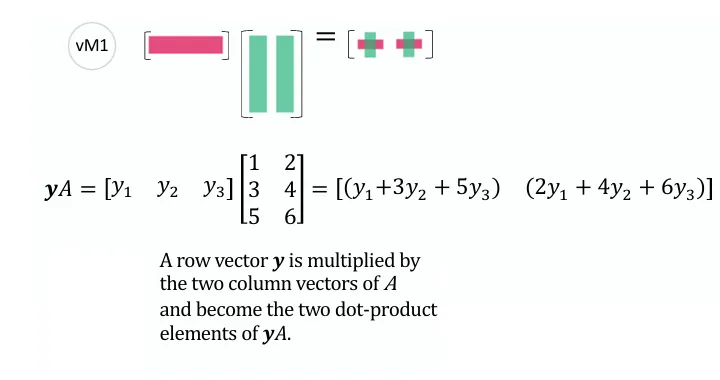
例如:A = [ 1 4 2 5 3 6 ] , y = [ y 1 y 2 y 3 ] A=\left[\begin{array}{ll}1 & 4 \\ 2 & 5 \\ 3 & 6\end{array}\right], \quad y =\left[\begin{array}{l}y_1 \\ y_2 \\ y_3\end{array}\right] A = 1 2 3 4 5 6 , y = y 1 y 2 y 3
矩阵乘法视角:
y T A = [ y 1 y 2 y 3 ] [ 1 4 2 5 3 6 ] = [ y 1 ⋅ 1 + y 2 ⋅ 2 + y 3 ⋅ 3 y 1 ⋅ 4 + y 2 ⋅ 5 + y 3 ⋅ 6 ] \begin{aligned}
& y ^{T} A=\left[\begin{array}{lll}
y_1 & y_2 & y_3
\end{array}\right]\left[\begin{array}{cc}
1 & 4 \\
2 & 5 \\
3 & 6
\end{array}\right] \\
& =\left[y_1 \cdot 1+y_2 \cdot 2+y_3 \cdot 3 \quad y_1 \cdot 4+y_2 \cdot 5+y_3 \cdot 6\right]
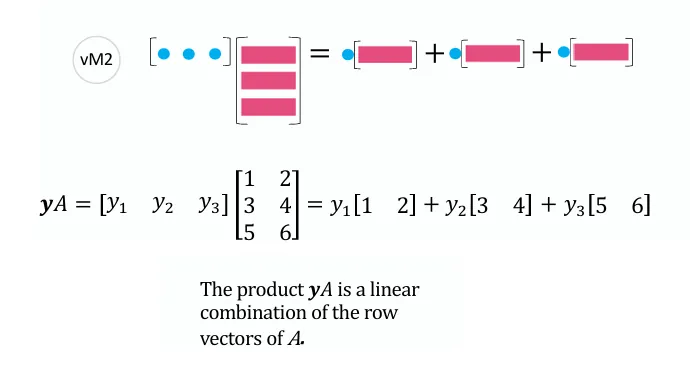
\end{aligned} y T A = [ y 1 y 2 y 3 ] 1 2 3 4 5 6 = [ y 1 ⋅ 1 + y 2 ⋅ 2 + y 3 ⋅ 3 y 1 ⋅ 4 + y 2 ⋅ 5 + y 3 ⋅ 6 ] 行向量线性组合视角:
y T A = [ y 1 y 2 y 3 ] [ 1 4 2 5 3 6 ] = y 1 [ 1 4 ] + y 2 [ 2 5 ] + y 3 [ 3 6 ] y ^{T} A=\left[\begin{array}{lll}
y_1 & y_2 & y_3
\end{array}\right]\left[\begin{array}{ll}
1 & 4 \\
2 & 5 \\
3 & 6
\end{array}\right]=y_1\left[\begin{array}{ll}
1 & 4
\end{array}\right]+y_2\left[\begin{array}{ll}
2 & 5
\end{array}\right]+y_3\left[\begin{array}{ll}
3 & 6
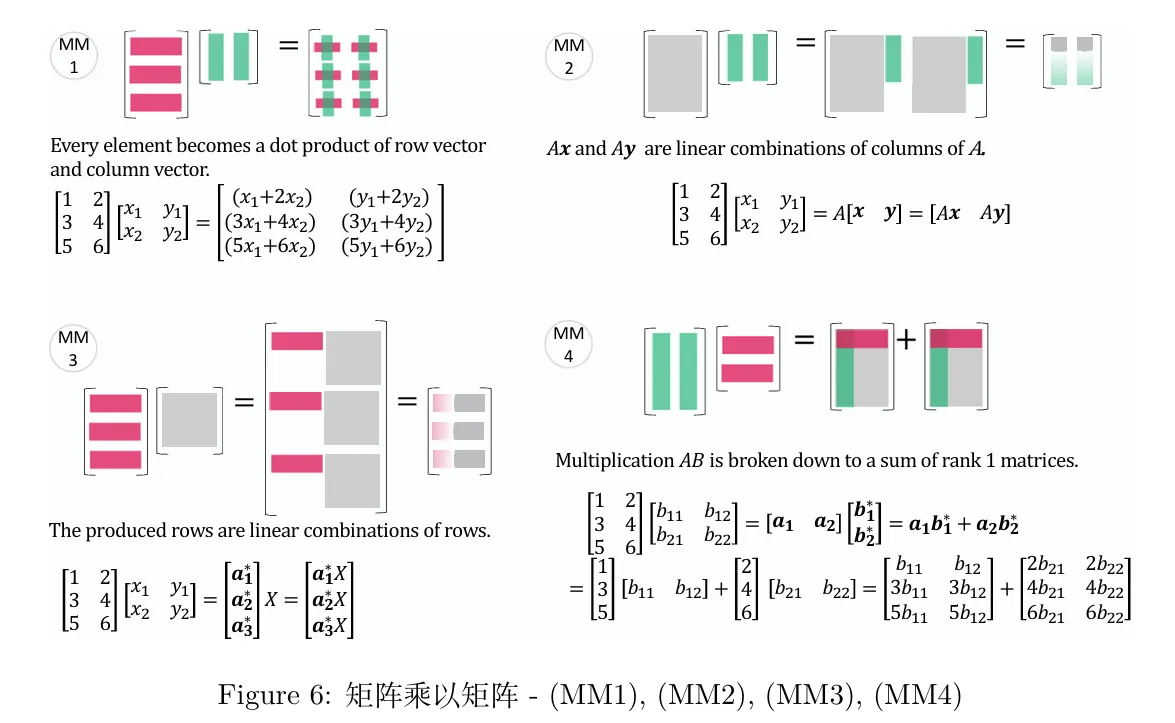
\end{array}\right] y T A = [ y 1 y 2 y 3 ] 1 2 3 4 5 6 = y 1 [ 1 4 ] + y 2 [ 2 5 ] + y 3 [ 3 6 ] 矩阵与矩阵相乘的四个视角 图中带∗ * ∗
(1)矩阵乘法定义(MM1)视角:根据矩阵乘法的定义来看矩阵乘法,其本质是 A A A B B B B B B A A A B B B A A A B B B A A A B B B A B A B A B A A A B B B A A A B B B m × n m \times n m × n
 {width=400px}
{width=400px}