引言
下课时间到了,在嘈杂的教室里,每个同学都在开心的大笑或者说话,但是在这种复杂的环境下,你闭着眼睛还是能够感觉到哪个是小明的声音,哪个是小强的声音。我们对这个现象已经习以为常,学过高中物理的我们知道,声音是一种波,每个人说的话都是一种声波,当多个声波在空气里传播时,彼此不受干扰,因此你能分辨初小明和小强的声音。矩阵乘法从本质上说与此类似,两个矩阵相乘,可以认为是对空间图形的线性变换。本节涉及到空间向量知识,如果对向量不了解,可以学过向量后,再来学习本文。
在矩阵变换里有3种重要变换,这里单独介绍一下。
缩放矩阵
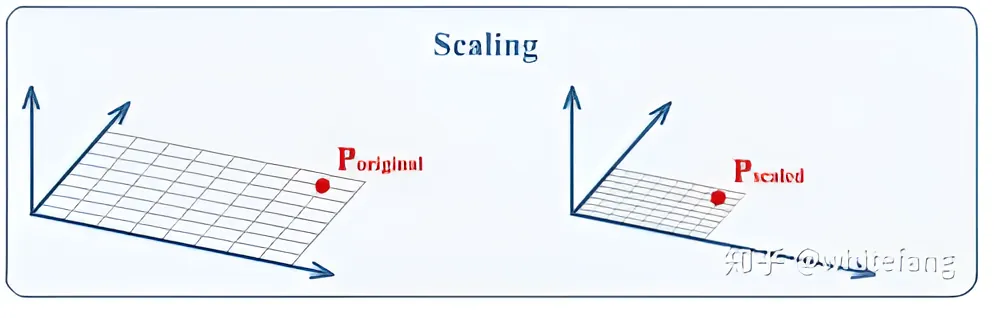
缩放变换中,如果一个图片以原点 (0,0) 为中心缩放 s 倍。那么点 (x,y) 变换后数学形式可以表示为
x′=sxy′=sy 写成矩阵形式为:
[x′y′]=[sx00sy][xy] 当然,我们也可以给 x 轴和 y 轴不同的缩放倍数 sx 和 sy 。在非均匀情况下,缩放变换的矩阵形式为
[x′y′]=[sx00sy][xy]...(图像缩放公式) 下图展示了图像缩放示意图
 {width=600px}
{width=600px}
仔细看上面这个矩阵,可以发现他是一个 对角形矩阵 即:主对角线有元素,其它元素都是0的矩阵,记住这种矩阵,他在线性变换里非常重要。
一个对角矩阵作用在一个三维向量 a=(1,2,3)上,相当于这个矩阵对这个向量的三个维度分别进行了变换。
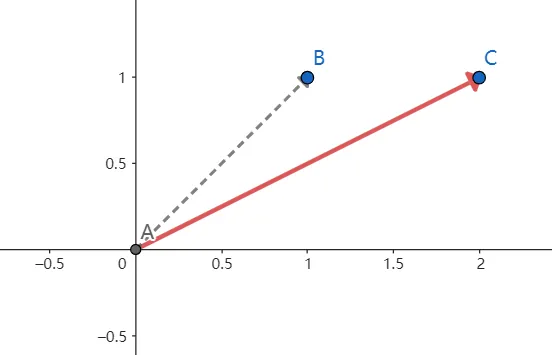
例 下面矩阵乘法显示一个向量[1,1] 左乘以一个对角矩阵后,变成 [2,1]
[2001][11]=[21] 从几何意义上看,向量从AB 变成AC ,也就是向量AB发生了放大和旋转。
对角矩阵的2相当于x方向上放大2倍,对角矩阵的1相当于y方向上放大1倍。
 {width=500px}
{width=500px}
旋转矩阵
我们默认旋转变换(Rotate)都绕着原点(0,0) 旋转,并且默认旋转方向为逆时针方向(逆时针方向旋转角度值为正,顺时针旋转角度值为负),当一个点 (x,y)绕着原点(0,0)旋转θ角时,变换矩阵可以表示为:
[x′y′]=[cosθsinθ−sinθcosθ][xy]...(图像旋转公式) 证明
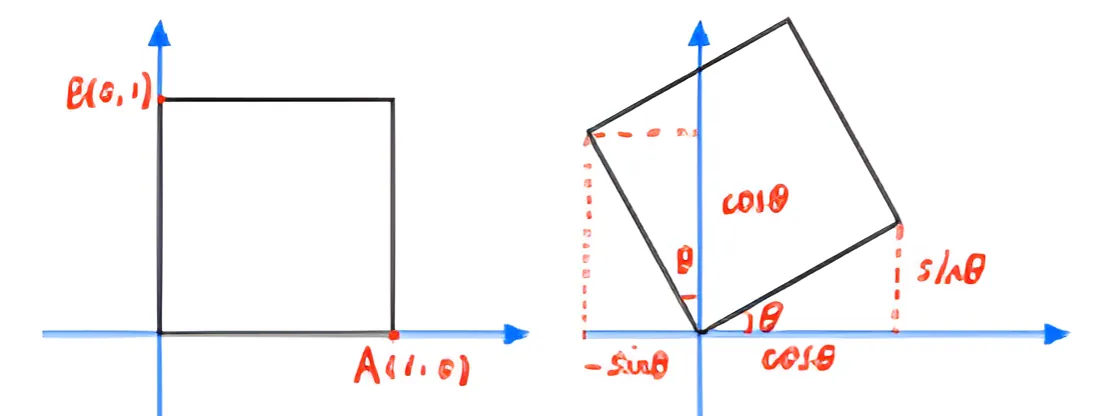
我们在直角坐标系中绘制一个边长为 1 的正方形,点 A 坐标为 (1,0) ,点 B 坐标为 (0,1) 。正方形沿着原点 (0,0) 旋转的角度为 θ 角 参考下图。
 {width=500px}
{width=500px}
我们设原坐标里任一点(x,y) 经过旋转后,在新坐标为(x′,y′),现在找一下新旧坐标系下“点”的关系。
[x′y′]=[ACBD][xy] 接下来去两个特殊点,代入点 A 的的值 (1,0) 可以得到:
[cosθsinθ]=[ACBD][10] 解方程得到:
A=cosθC=sinθ 代人点 B 的的值 (0,1) 可以得到:
[−sinθcosθ]=[ACBD][01] 解方程得到:
B=−sinθD=cosθ 因此,坐标旋转公式为
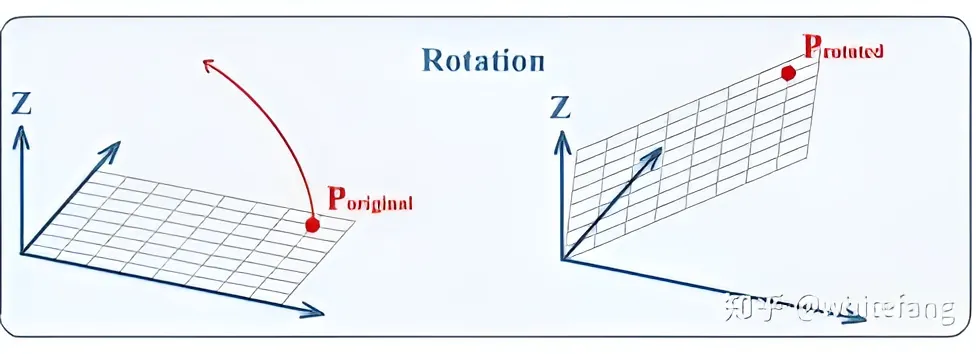
Arotate =[cosθsinθ−sinθcosθ] 下图显示了一个图形旋转
 {width=600px}
{width=600px}
例 考虑θ=45∘ 时, cosθ=sinθ=22 ,此时旋转矩阵A为
A=[2222−2222] 这意味着任何一个向量乘以该矩阵将旋转45∘
提示:默认旋转矩阵都是正交矩阵,其所对应的行列式的值是1或者-1,具体后面会介绍。
特别的考虑下面2个矩阵相乘是多少?
Arotate =2222−2222⋅Arotate =2222−2222=? Arotate ⋅Arotate 表示矩阵旋转两次,也就是角度为90度,不用计算,仔细思考上面结果是多少
上面可以推广到三维,例如
A=cosφsinφ0−sinφcosφ0001 就是空间图形绕Z周旋转矩阵。
切变矩阵
一本书实以水平的力,会发生切变
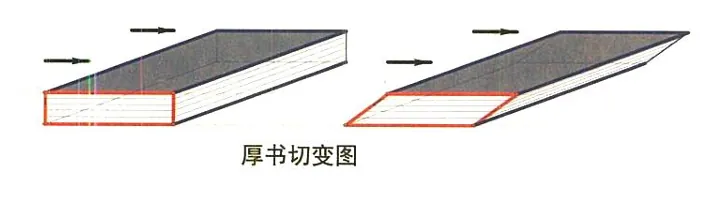
在平面上,一个正方形受到了一个 x1 轴方向的水平切变力,切变表现为,其力偶作用由正方形变成一个等底,等高的平行四边形。其中,点 P1(x1,x2) 为正方形的任意一点,点 P2(x1′,x2′) 是切变后 P1 点所对应的平移点。
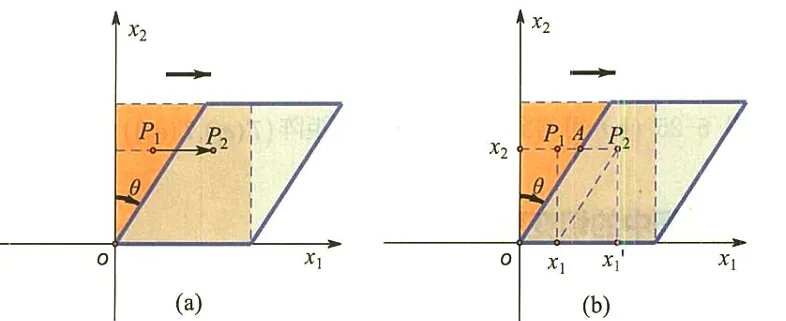
由切变的意义,在从点 P1 到点 P2 的切变过程中,纵坐标 x2(高度)不会发生变化,即 x2′=x2 ;横坐标 x1 会向右(力的方向)平移一段距离 P1P2 。如果把切变的变化量用一个变化的夹角来度量,就可以得到 P1P2=x2tanθ(见图(b),因为两个三角形全等:△oAx2≅Δx1P2P1 ),因此横坐标的变化关系为 x1′=x1+x2tanθ 。把 tanθ 简写为一个变量 k(k∈R) ,则有 {x1′=x1+kx2x2′=x2 ,将其改写成矩阵/向量的表达式
(x2′x1′)=[10k1](x2x1) 类似地,如果正方形切变的方向是竖直 x2 轴的方向,那么变化前后的坐标表达式为
{x1′=x1x2′=kx1+x2 或 (x2′x1′)=[1k01](x2x1) 因此,一个矩阵左乘矩阵 [10k1] 和 [1k01] 将发生切变。
我们称 [10k1] 为切变矩阵。
如果仔细观看,上面二维的可以推广到三维的,比如乘以
=10001k001 就是沿着y,z 方向切变
 {width=600px}
{width=600px} {width=500px}
{width=500px} {width=500px}
{width=500px} {width=600px}
{width=600px}
