矩阵的初等变换(理论证明) 这一节我们介绍一种求逆矩阵的方法,即初等变换的方法.对矩阵的行(列)进行下列三种变换,即矩阵的初等变换(elementary operations):
(1)对换变换——交换矩阵的两行(列)。
(2)数乘变换——将某行(列)全体元素都乘以某一非零常数。
(3)倍加变换——把某行(列)用该行(列)与另一行(列)的常数倍的和替换,也就是把另一行(列)的常数倍加到某行(列)上。
对 n n n E \boldsymbol{E} E E \boldsymbol{E} E i , j i, j i , j
(2)用 λ ( λ ≠ 0 ) \lambda(\lambda \neq 0) λ ( λ = 0 ) E \boldsymbol{E} E i i i
(3)将 E \boldsymbol{E} E j j j i i i γ \gamma γ i i i j j j ( i ≠ j ) (i \neq j) ( i = j )
引理 对矩阵左乘相当于是行变换,对矩阵右乘相当于是列变换
证明 仅以第三种初等行变换为例进行验证.
等式右端恰为对 A \boldsymbol{A} A
( P ( i , j ) ) − 1 = P ( i , j ) ( P ( i ( λ ) ) ) − 1 = P ( i ( 1 λ ) ) ( λ ≠ 0 ) ( P ( i , j ( γ ) ) ) − 1 = P ( i , j ( − γ ) ) \begin{aligned}
& (\boldsymbol{P}(i, j))^{-1}=\boldsymbol{P}(i, j) \\
& (\boldsymbol{P}(i(\lambda)))^{-1}=\boldsymbol{P}\left(i\left(\frac{1}{\lambda}\right)\right) \quad(\lambda \neq 0) \\
& (\boldsymbol{P}(i, j(\gamma)))^{-1}=\boldsymbol{P}(i, j(-\gamma))
\end{aligned} ( P ( i , j ) ) − 1 = P ( i , j ) ( P ( i ( λ )) ) − 1 = P ( i ( λ 1 ) ) ( λ = 0 ) ( P ( i , j ( γ )) ) − 1 = P ( i , j ( − γ )) 矩阵可逆的等价条件 定理 设 A \boldsymbol{A} A n n n A \boldsymbol{A} A A x = 0 \boldsymbol{A} \boldsymbol{x}=\mathbf{0} A x = 0 A \boldsymbol{A} A n n n E \boldsymbol{E} E A \boldsymbol{A} A E \boldsymbol{E} E
证明 我们首先证明(1)可推出(2).若 A \boldsymbol{A} A x \boldsymbol{x} x A x = 0 \boldsymbol{A} \boldsymbol{x}=\mathbf{0} A x = 0
x = E x = ( A − 1 A ) x = A − 1 ( A x ) = A − 1 0 = 0 \boldsymbol{x}=\boldsymbol{E} \boldsymbol{x}=\left(\boldsymbol{A}^{-1} \boldsymbol{A}\right) \boldsymbol{x}=\boldsymbol{A}^{-1}(\boldsymbol{A} \boldsymbol{x})=\boldsymbol{A}^{-1} \mathbf{0}=\mathbf{0} x = E x = ( A − 1 A ) x = A − 1 ( A x ) = A − 1 0 = 0 因此 A x = 0 \boldsymbol{A x}=\mathbf{0} Ax = 0 A x = 0 \boldsymbol{A x}=\mathbf{0} Ax = 0 A \boldsymbol{A} A n n n n n n A \boldsymbol{A} A n n n E \boldsymbol{E} E A \boldsymbol{A} A E , A \boldsymbol{E}, \boldsymbol{A} E , A E \boldsymbol{E} E
最后证明(3)可推出(1)。假设 A \boldsymbol{A} A E \boldsymbol{E} E A \boldsymbol{A} A P 1 , P 2 , ⋯ , P k \boldsymbol{P}_1, \boldsymbol{P}_2, \cdots, \boldsymbol{P}_k P 1 , P 2 , ⋯ , P k
P k P k − 1 ⋯ P 1 A = E . . . ( 2.3.2 ) \boldsymbol{P}_k \boldsymbol{P}_{k-1} \cdots \boldsymbol{P}_1 \boldsymbol{A}=\boldsymbol{E} ...(2.3.2) P k P k − 1 ⋯ P 1 A = E ... ( 2.3.2 ) 因为可逆矩阵的乘积 P k P k − 1 ⋯ P 1 \boldsymbol{P}_k \boldsymbol{P}_{k-1} \cdots \boldsymbol{P}_1 P k P k − 1 ⋯ P 1 P k P k − 1 ⋯ P 1 ) − 1 \boldsymbol{P}_k \boldsymbol{P}_{k-1} \cdots \left.\boldsymbol{P}_1\right)^{-1} P k P k − 1 ⋯ P 1 ) − 1
即
( P k P k − 1 ⋯ P 1 ) − 1 ( P k P k − 1 ⋯ P 1 ) A = ( P k P k − 1 ⋯ P 1 ) − 1 E , \left(\boldsymbol{P}_k \boldsymbol{P}_{k-1} \cdots \boldsymbol{P}_1\right)^{-1}\left(\boldsymbol{P}_k \boldsymbol{P}_{k-1} \cdots \boldsymbol{P}_1\right) \boldsymbol{A}=\left(\boldsymbol{P}_k \boldsymbol{P}_{k-1} \cdots \boldsymbol{P}_1\right)^{-1} \boldsymbol{E}, ( P k P k − 1 ⋯ P 1 ) − 1 ( P k P k − 1 ⋯ P 1 ) A = ( P k P k − 1 ⋯ P 1 ) − 1 E , 即
A = ( P k P k − 1 ⋯ P 1 ) − 1 \boldsymbol{A}=\left(\boldsymbol{P}_k \boldsymbol{P}_{k-1} \cdots \boldsymbol{P}_1\right)^{-1} A = ( P k P k − 1 ⋯ P 1 ) − 1 因此 A \boldsymbol{A} A A \boldsymbol{A} A
推论 2.3.2 下列命题等价:
(1)方阵 A \boldsymbol{A} A A \boldsymbol{A} A A \boldsymbol{A} A n n n
推论2.3.2 下列命题等价:
(1)方阵 A \boldsymbol{A} A A \boldsymbol{A} A A \boldsymbol{A} A n n n
推论2.3.3 若 n n n A \boldsymbol{A} A B \boldsymbol{B} B A \boldsymbol{A} A B \boldsymbol{B} B
从上面的证明过程中我们可以得到 A \boldsymbol{A} A A − 1 \boldsymbol{A}^{-1} A − 1
A − 1 = [ ( P k P k − 1 ⋯ P 1 ) − 1 ] − 1 = P k P k − 1 ⋯ P 1 = P k P k − 1 ⋯ P 1 E . \begin{aligned}
\boldsymbol{A}^{-1} & =\left[\left(\boldsymbol{P}_k \boldsymbol{P}_{k-1} \cdots \boldsymbol{P}_1\right)^{-1}\right]^{-1} \\
& =\boldsymbol{P}_k \boldsymbol{P}_{k-1} \cdots \boldsymbol{P}_1 \\
& =\boldsymbol{P}_k \boldsymbol{P}_{k-1} \cdots \boldsymbol{P}_1 \boldsymbol{E} .
\end{aligned} A − 1 = [ ( P k P k − 1 ⋯ P 1 ) − 1 ] − 1 = P k P k − 1 ⋯ P 1 = P k P k − 1 ⋯ P 1 E . 这说明 A − 1 \boldsymbol{A}^{-1} A − 1 P k P k − 1 ⋯ P 1 \boldsymbol{P}_k \boldsymbol{P}_{k-1} \cdots \boldsymbol{P}_1 P k P k − 1 ⋯ P 1 n n n E \boldsymbol{E} E A \boldsymbol{A} A
P k P k − 1 ⋯ P 1 A = E . . . ( 2.3.3 ) P k P k − 1 ⋯ P 1 E = A − 1 . . . ( 2.3.4 ) \begin{gathered}
\boldsymbol{P}_k \boldsymbol{P}_{k-1} \cdots \boldsymbol{P}_1 \boldsymbol{A}=\boldsymbol{E} ...(2.3.3)\\
\boldsymbol{P}_k \boldsymbol{P}_{k-1} \cdots \boldsymbol{P}_1 \boldsymbol{E}=\boldsymbol{A}^{-1} ...(2.3.4)
\end{gathered} P k P k − 1 ⋯ P 1 A = E ... ( 2.3.3 ) P k P k − 1 ⋯ P 1 E = A − 1 ... ( 2.3.4 ) 比较(2.3.3)和(2.3.4)可知,若对 A \boldsymbol{A} A E \boldsymbol{E} E A \boldsymbol{A} A E \boldsymbol{E} E E \boldsymbol{E} E A \boldsymbol{A} A A − 1 \boldsymbol{A}^{-1} A − 1 A \boldsymbol{A} A n × 2 n n \times 2 n n × 2 n ( A ∣ E ) (\boldsymbol{A} \mid \boldsymbol{E}) ( A ∣ E ) A \boldsymbol{A} A E \boldsymbol{E} E A − 1 \boldsymbol{A}^{-1} A − 1
初等矩阵 对 n n n E \boldsymbol{E} E n n n
例 设 A = ( a i j ) A=\left(a_{i j}\right) A = ( a ij ) P \boldsymbol{P} P
P A = ( a 11 a 12 a 13 a 31 + k a 11 a 32 + k a 12 a 33 + k a 13 a 21 a 22 a 23 ) . \boldsymbol{P A}=\left(\begin{array}{ccc}
a_{11} & a_{12} & a_{13} \\
a_{31}+k a_{11} & a_{32}+k a_{12} & a_{33}+k a_{13} \\
a_{21} & a_{22} & a_{23}
\end{array}\right) . PA = a 11 a 31 + k a 11 a 21 a 12 a 32 + k a 12 a 22 a 13 a 33 + k a 13 a 23 . 解:矩阵 P A P A P A A = ( a v ) A=\left(a_v\right) A = ( a v ) A A A A A A k k k E ( 2 , 3 ) = ( 1 0 0 0 0 1 0 1 0 ) 、 E ( ( k ) , 2 ) = ( 1 0 0 k 1 0 0 0 1 ) E(2,3)=\left(\begin{array}{lll}1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0\end{array}\right) 、 E((k), 2)=\left(\begin{array}{lll}1 & 0 & 0 \\ k & 1 & 0 \\ 0 & 0 & 1\end{array}\right) E ( 2 , 3 ) = 1 0 0 0 0 1 0 1 0 、 E (( k ) , 2 ) = 1 k 0 0 1 0 0 0 1 A \boldsymbol{A} A P A = E ( 1 ( k ) , 2 ) E ( 2 , 3 ) A , P A=E(1(k), 2) E(2,3) A , P A = E ( 1 ( k ) , 2 ) E ( 2 , 3 ) A ,
P = E ( 1 ( k ) , 2 ) E ( 2 , 3 ) = ( 1 0 0 k 1 0 0 0 1 ) ( 1 0 0 0 0 1 0 1 0 ) = ( 1 0 0 k 0 1 0 1 0 ) . P=E(1(k), 2) E(2,3)=\left(\begin{array}{lll}
1 & 0 & 0 \\
k & 1 & 0 \\
0 & 0 & 1
\end{array}\right)\left(\begin{array}{lll}
1 & 0 & 0 \\
0 & 0 & 1 \\
0 & 1 & 0
\end{array}\right)=\left(\begin{array}{lll}
1 & 0 & 0 \\
k & 0 & 1 \\
0 & 1 & 0
\end{array}\right) . P = E ( 1 ( k ) , 2 ) E ( 2 , 3 ) = 1 k 0 0 1 0 0 0 1 1 0 0 0 0 1 0 1 0 = 1 k 0 0 0 1 0 1 0 . 另外,矩阵 P A P A P A A = ( a j ) A=\left(a_j\right) A = ( a j ) A A A k k k A A A P A = E ( 2 , 3 ) E ( 1 ( k ) , 3 ) A \boldsymbol{P A}=\boldsymbol{E}(2,3) \boldsymbol{E}(1(k), 3) \boldsymbol{A} PA = E ( 2 , 3 ) E ( 1 ( k ) , 3 ) A
利用初等变换求解矩阵的逆矩阵 把一个矩阵和单位矩阵进行合并,然后进行行变换,左边化为单位矩阵,右边就是矩阵的逆,即
( A ∣ E ) → 初等行变换 ( E ∣ A − 1 ) (\boldsymbol{A} \mid \boldsymbol{E}) \xrightarrow{\text { 初等行变换 }}\left(\boldsymbol{E} \mid \boldsymbol{A}^{-1}\right) ( A ∣ E ) 初等行变换 ( E ∣ A − 1 )
例 求逆矩阵
( 1 1 − 2 2 − 1 − 1 3 6 − 9 ) \left(\begin{array}{ccc}
1 & 1 & -2 \\
2 & -1 & -1 \\
3 & 6 & -9
\end{array}\right) 1 2 3 1 − 1 6 − 2 − 1 − 9 解:
( 1 1 − 2 1 0 0 2 − 1 − 1 0 1 0 3 6 − 9 0 0 1 ) \left(\begin{array}{ccc|ccc}
1 & 1 & -2 & 1 & 0 & 0 \\
2 & -1 & -1 & 0 & 1 & 0 \\
3 & 6 & -9 & 0 & 0 & 1
\end{array}\right) 1 2 3 1 − 1 6 − 2 − 1 − 9 1 0 0 0 1 0 0 0 1 ∼ ( 1 1 − 2 1 0 0 0 − 3 3 − 2 1 0 0 3 − 3 − 3 0 1 ) \sim \left(\begin{array}{ccc|ccc}
1 & 1 & -2 & 1 & 0 & 0 \\
0 & -3 & 3 & -2 & 1 & 0 \\
0 & 3 & -3 & -3 & 0 & 1
\end{array}\right) ∼ 1 0 0 1 − 3 3 − 2 3 − 3 1 − 2 − 3 0 1 0 0 0 1 ∼ ( 1 1 − 2 1 0 0 0 − 3 3 − 2 1 0 0 0 0 − 5 1 1 ) \sim \left(\begin{array}{ccc|ccc}
1 & 1 & -2 & 1 & 0 & 0 \\
0 & -3 & 3 & -2 & 1 & 0 \\
0 & 0 & 0 & -5 & 1 & 1
\end{array}\right) ∼ 1 0 0 1 − 3 0 − 2 3 0 1 − 2 − 5 0 1 1 0 0 1 由于最后一行左侧全是0,所以矩阵不可逆。
例 求逆矩阵
( 1 1 1 1 2 3 1 3 6 ) \left(\begin{array}{lll}
1 & 1 & 1 \\
1 & 2 & 3 \\
1 & 3 & 6
\end{array}\right) 1 1 1 1 2 3 1 3 6 解:
( 1 1 1 1 0 0 1 2 3 0 1 0 1 3 6 0 0 1 ) \left(\begin{array}{lll|lll}
1 & 1 & 1 & 1 & 0 & 0 \\
1 & 2 & 3 & 0 & 1 & 0 \\
1 & 3 & 6 & 0 & 0 & 1
\end{array}\right) 1 1 1 1 2 3 1 3 6 1 0 0 0 1 0 0 0 1 ∼ ( 1 1 1 1 0 0 0 1 2 − 1 1 0 0 0 1 1 − 2 1 ) \sim \left(\begin{array}{ccc|ccc}
1 & 1 & 1 & 1 & 0 & 0 \\
0 & 1 & 2 & -1 & 1 & 0 \\
0 & 0 & 1 & 1 & -2 & 1
\end{array}\right) ∼ 1 0 0 1 1 0 1 2 1 1 − 1 1 0 1 − 2 0 0 1 ∼ ( 1 0 0 3 − 3 1 0 1 0 − 3 5 − 2 0 0 1 1 − 2 1 ) \sim \left(\begin{array}{ccc|ccc}
1 & 0 & 0 & 3 & -3 & 1 \\
0 & 1 & 0 & -3 & 5 & -2 \\
0 & 0 & 1 & 1 & -2 & 1
\end{array}\right) ∼ 1 0 0 0 1 0 0 0 1 3 − 3 1 − 3 5 − 2 1 − 2 1 所以矩阵可逆,且逆矩阵为
A − 1 = ( 3 − 3 1 − 3 5 − 2 1 − 2 1 ) A^{-1}=\left(\begin{array}{ccc}
3 & -3 & 1 \\
-3 & 5 & -2 \\
1 & -2 & 1
\end{array}\right) A − 1 = 3 − 3 1 − 3 5 − 2 1 − 2 1 利用逆矩阵解方程 利用逆矩阵还可以求解矩阵方程
① A X = B ①A X=B ① A X = B ② X A = B ②X A=B ② X A = B ③ A X B = C ③A X B=C ③ A XB = C
具体求解为
①若矩阵 A A A
A − 1 ( A X ) = A − 1 B ⇒ ( A − 1 A ) X = A − 1 B ⇒ X = A − 1 B . A^{-1}(A X)=A^{-1} B \Rightarrow\left(A^{-1} A\right) X=A^{-1} B \Rightarrow X=A^{-1} B . A − 1 ( A X ) = A − 1 B ⇒ ( A − 1 A ) X = A − 1 B ⇒ X = A − 1 B . ②若矩阵 A A A
( X A ) A − 1 = B A − 1 ⇒ X ( A A − 1 ) = B A − 1 ⇒ X = B A − 1 . (\mathrm{X} A) A^{-1}=B A^{-1} \Rightarrow X\left(A A^{-1}\right)=B A^{-1} \Rightarrow X=B A^{-1} . ( X A ) A − 1 = B A − 1 ⇒ X ( A A − 1 ) = B A − 1 ⇒ X = B A − 1 . ③若矩阵 A 、 B A 、 B A 、 B
A − 1 ( A X B ) B − 1 = A − 1 C B − 1 ⇒ ( A − 1 A ) X ( B B − 1 ) = A − 1 C B − 1 ⇒ X = A − 1 C B − 1 . A^{-1}(A X B) B^{-1}=A^{-1} C B^{-1} \Rightarrow\left(A^{-1} A\right) X\left(B B^{-1}\right)=A^{-1} C B^{-1} \Rightarrow X=A^{-1} C B^{-1} . A − 1 ( A XB ) B − 1 = A − 1 C B − 1 ⇒ ( A − 1 A ) X ( B B − 1 ) = A − 1 C B − 1 ⇒ X = A − 1 C B − 1 . 所以,可以用初等行变换的方法解矩阵方程.
解方程步骤
①首先构造分块矩阵 ( A ∣ B ) (\boldsymbol{A} \mid \boldsymbol{B}) ( A ∣ B ) ( A ∣ B ) (\boldsymbol{A} \mid \boldsymbol{B}) ( A ∣ B ) ( A ∣ B ) (\boldsymbol{A} \mid \boldsymbol{B}) ( A ∣ B ) A \boldsymbol{A} A E \boldsymbol{E} E A \boldsymbol{A} A B \boldsymbol{B} B X = A − 1 B \boldsymbol{X}=\boldsymbol{A}^{-1} \boldsymbol{B} X = A − 1 B
例 解方程
( − 1 4 − 2 7 ) X = ( 2 − 1 3 1 0 − 2 ) \left(\begin{array}{ll}
-1 & 4 \\
-2 & 7
\end{array}\right) \boldsymbol{X}=\left(\begin{array}{ccc}
2 & -1 & 3 \\
1 & 0 & -2
\end{array}\right) ( − 1 − 2 4 7 ) X = ( 2 1 − 1 0 3 − 2 ) 解:
( − 1 4 2 − 1 3 − 2 7 1 0 − 2 ) \left(\begin{array}{cc|ccc}
-1 & 4 & 2 & -1 & 3 \\
-2 & 7 & 1 & 0 & -2
\end{array}\right) ( − 1 − 2 4 7 2 1 − 1 0 3 − 2 ) ∼ → ( 1 − 4 − 2 1 − 3 0 − 1 − 3 2 − 8 ) \sim
\rightarrow\left(\begin{array}{ll|lll}
1 & -4 & -2 & 1 & -3 \\
0 & -1 & -3 & 2 & -8
\end{array}\right) ∼→ ( 1 0 − 4 − 1 − 2 − 3 1 2 − 3 − 8 ) ∼ ( 1 0 10 − 7 29 0 1 3 − 2 8 ) \sim
\left(\begin{array}{cc|ccc}
1 & 0 & 10 & -7 & 29 \\
0 & 1 & 3 & -2 & 8
\end{array}\right) ∼ ( 1 0 0 1 10 3 − 7 − 2 29 8 ) 所以方程的解为
X = ( 10 − 7 29 3 − 2 8 ) \boldsymbol{X}=\left(\begin{array}{ccc}
10 & -7 & 29 \\
3 & -2 & 8
\end{array}\right) X = ( 10 3 − 7 − 2 29 8 ) 例 解方程
X ( 1 0 − 2 0 − 2 1 − 2 − 1 5 ) = ( − 1 1 0 1 2 − 1 ) \boldsymbol{X}\left(\begin{array}{ccc}
1 & 0 & -2 \\
0 & -2 & 1 \\
-2 & -1 & 5
\end{array}\right)=\left(\begin{array}{ccc}
-1 & 1 & 0 \\
1 & 2 & -1
\end{array}\right) X 1 0 − 2 0 − 2 − 1 − 2 1 5 = ( − 1 1 1 2 0 − 1 ) 对于方程 X A = B X A=B X A = B A T X T = B T A^{\mathrm{T}} X^{\mathrm{T}}=B^{\mathrm{T}} A T X T = B T X X X
解:
( A T ∣ B T ) = ( 1 0 − 2 − 1 1 0 − 2 − 1 1 2 − 2 1 5 0 − 1 ) \left(\boldsymbol{A}^{\mathrm{T}} \mid \boldsymbol{B}^{\mathrm{T}}\right)=\left(\begin{array}{ccc|cc}
1 & 0 & -2 & -1 & 1 \\
0 & -2 & -1 & 1 & 2 \\
-2 & 1 & 5 & 0 & -1
\end{array}\right) ( A T ∣ B T ) = 1 0 − 2 0 − 2 1 − 2 − 1 5 − 1 1 0 1 2 − 1 ∼ ( 1 0 − 2 − 1 1 0 − 2 − 1 1 2 0 1 1 − 2 1 ) \sim
\left(\begin{array}{ccc|cc}
1 & 0 & -2 & -1 & 1 \\
0 & -2 & -1 & 1 & 2 \\
0 & 1 & 1 & -2 & 1
\end{array}\right) ∼ 1 0 0 0 − 2 1 − 2 − 1 1 − 1 1 − 2 1 2 1 ∼ ( 1 0 − 2 − 1 1 0 1 1 − 2 1 0 0 1 − 3 4 ) \sim
\left(\begin{array}{ccc|cc}
1 & 0 & -2 & -1 & 1 \\
0 & 1 & 1 & -2 & 1 \\
0 & 0 & 1 & -3 & 4
\end{array}\right) ∼ 1 0 0 0 1 0 − 2 1 1 − 1 − 2 − 3 1 1 4 ∼ ( 1 0 0 − 7 9 0 1 0 1 − 3 0 0 1 − 3 4 ) \sim
\left(\begin{array}{ccc|cc}
1 & 0 & 0 & -7 & 9 \\
0 & 1 & 0 & 1 & -3 \\
0 & 0 & 1 & -3 & 4
\end{array}\right) ∼ 1 0 0 0 1 0 0 0 1 − 7 1 − 3 9 − 3 4 所以 X T = ( − 7 9 1 − 3 − 3 4 ) \boldsymbol{X}^{\mathrm{T}}=\left(\begin{array}{cc}-7 & 9 \\ 1 & -3 \\ -3 & 4\end{array}\right) \quad X T = − 7 1 − 3 9 − 3 4 X = ( − 7 1 − 3 9 − 3 4 ) \boldsymbol{X}=\left(\begin{array}{ccc}-7 & 1 & -3 \\ 9 & -3 & 4\end{array}\right) X = ( − 7 9 1 − 3 − 3 4 )
例 解方程
( 1 1 − 1 − 2 ) X ( − 1 1 0 0 1 − 1 1 0 − 2 ) = ( 1 − 1 0 − 1 0 1 ) \left(\begin{array}{cc}
1 & 1 \\
-1 & -2
\end{array}\right) \boldsymbol{X}\left(\begin{array}{ccc}
-1 & 1 & 0 \\
0 & 1 & -1 \\
1 & 0 & -2
\end{array}\right)=\left(\begin{array}{ccc}
1 & -1 & 0 \\
-1 & 0 & 1
\end{array}\right) ( 1 − 1 1 − 2 ) X − 1 0 1 1 1 0 0 − 1 − 2 = ( 1 − 1 − 1 0 0 1 ) 解:此题是 A X B = C \boldsymbol{A} \boldsymbol{X B}=\boldsymbol{C} A XB = C X B = Y \boldsymbol{X B}=\boldsymbol{Y} XB = Y A Y = C \boldsymbol{A Y}=\boldsymbol{C} AY = C B T X T = Y T \boldsymbol{B}^{\mathrm{T}} \boldsymbol{X}^{\mathrm{T}}=\boldsymbol{Y}^{\mathrm{T}} B T X T = Y T X \boldsymbol{X} X
( A ∣ C ) = ( 1 1 1 − 1 0 − 1 − 2 − 1 0 1 ) → r 2 + r 1 ( 1 1 1 − 1 0 0 − 1 0 − 1 1 ) → ( − 1 ) r 2 r 1 + r 2 ( 1 0 1 − 2 1 0 1 0 1 − 1 ) (\boldsymbol{A} \mid \boldsymbol{C})=\left(\begin{array}{cc|ccc}
1 & 1 & 1 & -1 & 0 \\
-1 & -2 & -1 & 0 & 1
\end{array}\right) \xrightarrow{r_2+r_1}\left(\begin{array}{cc|ccc}
1 & 1 & 1 & -1 & 0 \\
0 & -1 & 0 & -1 & 1
\end{array}\right) \xrightarrow[(-1) r_2]{r_1+r_2}\left(\begin{array}{cc|ccc}
1 & 0 & 1 & -2 & 1 \\
0 & 1 & 0 & 1 & -1
\end{array}\right) ( A ∣ C ) = ( 1 − 1 1 − 2 1 − 1 − 1 0 0 1 ) r 2 + r 1 ( 1 0 1 − 1 1 0 − 1 − 1 0 1 ) r 1 + r 2 ( − 1 ) r 2 ( 1 0 0 1 1 0 − 2 1 1 − 1 ) 于是得 Y = ( 1 − 2 1 0 1 − 1 ) \boldsymbol{Y}=\left(\begin{array}{ccc}1 & -2 & 1 \\ 0 & 1 & -1\end{array}\right) Y = ( 1 0 − 2 1 1 − 1 )
( B T ∣ Y T ) = ( − 1 0 1 1 0 1 1 0 − 2 1 0 − 1 − 2 1 − 1 ) → r 2 + r 1 ( − 1 0 1 1 0 0 1 1 − 1 1 0 − 1 − 2 1 − 1 ) → ( − 1 ) h r 3 + r 2 ( − 1 0 1 1 0 0 1 1 − 1 1 0 0 1 0 0 ) → r 2 + ( − 1 ) r n r 2 ( − 1 ) r 5 ( − 1 ) r n ( 1 0 0 − 1 0 0 1 0 − 1 1 0 0 1 0 0 ) \left(\boldsymbol{B}^{\mathrm{T}} \mid \boldsymbol{Y}^{\mathrm{T}}\right)=\left(\begin{array}{ccc|cc}
-1 & 0 & 1 & 1 & 0 \\
1 & 1 & 0 & -2 & 1 \\
0 & -1 & -2 & 1 & -1
\end{array}\right) \xrightarrow{r_2+r_1}\left(\begin{array}{ccc|cc}
-1 & 0 & 1 & 1 & 0 \\
0 & 1 & 1 & -1 & 1 \\
0 & -1 & -2 & 1 & -1
\end{array}\right) \xrightarrow[(-1) h]{r_3+r_2}\left(\begin{array}{ccc|cc}
-1 & 0 & 1 & 1 & 0 \\
0 & 1 & 1 & -1 & 1 \\
0 & 0 & 1 & 0 & 0
\end{array}\right) \xrightarrow[r_2+(-1) r_n]{\substack{r_2(-1) r_5 \\
(-1) r_n}}\left(\begin{array}{ccc|cc}
1 & 0 & 0 & -1 & 0 \\
0 & 1 & 0 & -1 & 1 \\
0 & 0 & 1 & 0 & 0
\end{array}\right) ( B T ∣ Y T ) = − 1 1 0 0 1 − 1 1 0 − 2 1 − 2 1 0 1 − 1 r 2 + r 1 − 1 0 0 0 1 − 1 1 1 − 2 1 − 1 1 0 1 − 1 r 3 + r 2 ( − 1 ) h − 1 0 0 0 1 0 1 1 1 1 − 1 0 0 1 0 r 2 ( − 1 ) r 5 ( − 1 ) r n r 2 + ( − 1 ) r n 1 0 0 0 1 0 0 0 1 − 1 − 1 0 0 1 0 可知 X T = ( − 1 0 − 1 1 0 0 ) \boldsymbol{X}^{\mathrm{T}}=\left(\begin{array}{cc}-1 & 0 \\ -1 & 1 \\ 0 & 0\end{array}\right) X T = − 1 − 1 0 0 1 0 X = ( − 1 − 1 0 0 1 0 ) \boldsymbol{X}=\left(\begin{array}{ccc}-1 & -1 & 0 \\ 0 & 1 & 0\end{array}\right) X = ( − 1 0 − 1 1 0 0 )
 {width=400px}
{width=400px}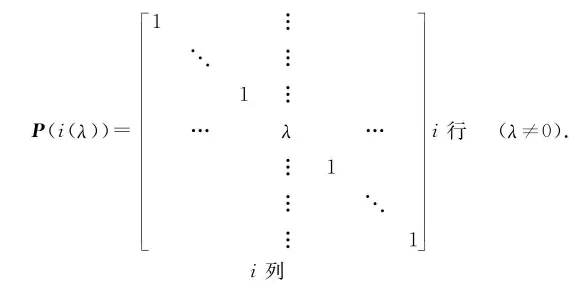 {width=400px}
{width=400px}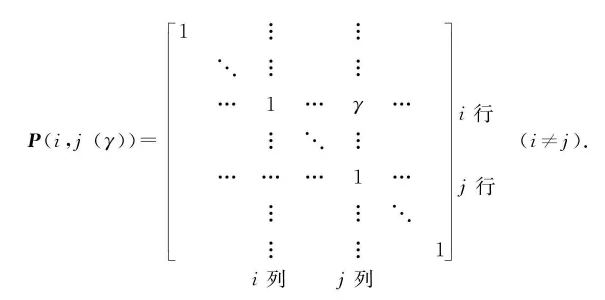 {width=400px}
{width=400px} {width=500px}
{width=500px}