对于初学线性代数的人,遇到的第一个抽象的概念就是:矩阵的秩,矩阵的秩太重要了,后面很多结论都需要用它,本文介绍矩阵的秩的定义和意义。在阅读本节内容前,需要先了解阶梯形矩阵 ,要从向量空间理解矩阵的秩,请点击矩阵的秩(向量版)
矩阵的秩的引入 本文谈谈矩阵秩的概念,先看一个例题:解下列线性方程组的解,
{ x 1 − 2 x 2 − x 3 + 3 x 4 = 1 2 x 1 − 4 x 2 + x 3 = 5 x 1 − 2 x 2 + 2 x 3 − 3 x 4 = 4 \left\{\begin{aligned}
&x_1-2 x_2-x_3+3 x_4 & =1 \\
&2 x_1-4 x_2+x_3 & =5 \\
&x_1-2 x_2+2 x_3-3 x_4 & =4
\end{aligned}
\right. ⎩ ⎨ ⎧ x 1 − 2 x 2 − x 3 + 3 x 4 2 x 1 − 4 x 2 + x 3 x 1 − 2 x 2 + 2 x 3 − 3 x 4 = 1 = 5 = 4 我们按高斯消元法,首先列出增广矩阵:
[ 1 − 2 − 1 3 1 2 − 4 1 0 5 1 − 2 2 − 3 4 ] \left[\begin{array}{rrrr|r}
1 & -2 & -1 & 3 & 1 \\
2 & -4 & 1 & 0 & 5 \\
1 & -2 & 2 & -3 & 4
\end{array}\right] 1 2 1 − 2 − 4 − 2 − 1 1 2 3 0 − 3 1 5 4 现在把他化为阶梯形矩阵。
(i) 用第一行的-2倍加到第二行
(ii)用第一行的-1倍加到第三行
[ 1 − 2 − 1 3 1 0 0 3 − 6 3 0 0 3 − 6 3 ] \left[\begin{array}{rrrr|r}
1 & -2 & -1 & 3 & 1 \\
0 & 0 & 3 & -6 & 3 \\
0 & 0 & 3 & -6 & 3
\end{array}\right] 1 0 0 − 2 0 0 − 1 3 3 3 − 6 − 6 1 3 3 继续化简,
(i)用第二行的-1倍加到第三行
(ii)第二行乘以1 3 \frac{1}{3} 3 1
如果我们把上面矩阵系数再还原成方程,则是:
{ x 1 − 2 x 2 − x 3 + 3 x 4 = 1 0 x 1 + 0 x 2 + x 3 − 2 x 4 = 1 0 x 1 + 0 x 2 + 0 x 3 + 0 x 4 = 0 \left\{\begin{aligned}
&x_1-2 x_2-x_3+3 x_4 & =1 \\
&0 x_1+0 x_2+x_3 -2x_4 & =1 \\
&0 x_1+0 x_2+0 x_3+0 x_4 & =0
\end{aligned}
\right. ⎩ ⎨ ⎧ x 1 − 2 x 2 − x 3 + 3 x 4 0 x 1 + 0 x 2 + x 3 − 2 x 4 0 x 1 + 0 x 2 + 0 x 3 + 0 x 4 = 1 = 1 = 0 仔细观察上面第三个方程,可以发现,不论x x x
因此,如何求矩阵的秩?我们要牢记下面一个结论:
给你一个矩阵,把他化为阶梯形,数一下阶梯的行数,有几行矩阵的秩就是几。
从这里,还可以得到一个结论:
矩阵的秩的本质就是:给你一个方程组,其中有效的方程的个数。
矩阵的行与列 仍以上面方程组为例
{ x 1 − 2 x 2 − x 3 + 3 x 4 = 1 2 x 1 − 4 x 2 + x 3 = 5 x 1 − 2 x 2 + 2 x 3 − 3 x 4 = 4 . . . ( 3.5 ) \left\{\begin{aligned}
&x_1-2 x_2-x_3+3 x_4 & =1 \\
&2 x_1-4 x_2+x_3 & =5 \\
&x_1-2 x_2+2 x_3-3 x_4 & =4
\end{aligned}
\right. ...(3.5) ⎩ ⎨ ⎧ x 1 − 2 x 2 − x 3 + 3 x 4 2 x 1 − 4 x 2 + x 3 x 1 − 2 x 2 + 2 x 3 − 3 x 4 = 1 = 5 = 4 ... ( 3.5 ) 前面介绍过分块矩阵,把矩阵按照一列列进行分块,则可以表示为
x 1 [ 1 2 1 ] + x 2 [ − 2 − 4 − 2 ] + x 3 [ − 1 1 2 ] + x 4 [ 3 0 − 3 ] = [ 1 5 4 ] . . . ( 3.6 ) x_1 \left[\begin{array}{l}
1 \\
2 \\
1
\end{array}\right] +x_2 \left[\begin{array}{l}
-2 \\
-4 \\
-2
\end{array}\right]+x_3\left[\begin{array}{r}
-1 \\
1 \\
2
\end{array}\right]+x_4\left[\begin{array}{r}
3 \\
0 \\
-3
\end{array}\right]=\left[\begin{array}{r}
1 \\
5 \\
4
\end{array}\right] ...(3.6) x 1 1 2 1 + x 2 − 2 − 4 − 2 + x 3 − 1 1 2 + x 4 3 0 − 3 = 1 5 4 ... ( 3.6 ) 把3.6 等号两端都取转置并考虑x i x_i x i
x 1 [ 1 2 1 ] + x 2 [ − 2 − 4 − 2 ] + x 3 [ − 1 1 2 ] + x 4 [ 3 0 − 3 ] = [ 1 5 4 ] . . . ( 3.7 ) x_1 \left[\begin{array}{l}1 \quad 2 \quad 1\end{array}\right] +x_2 \left[\begin{array}{l}-2 \quad -4 \quad -2 \end{array}\right]+x_3\left[\begin{array}{r}
-1 \quad 1 \quad 2 \end{array}\right]+x_4\left[\begin{array}{r}3 \quad 0 \quad -3\end{array}\right]=\left[\begin{array}{r}1 \quad 5\quad 4\end{array}\right] ...(3.7) x 1 [ 1 2 1 ] + x 2 [ − 2 − 4 − 2 ] + x 3 [ − 1 1 2 ] + x 4 [ 3 0 − 3 ] = [ 1 5 4 ] ... ( 3.7 ) 从上面可以看到(3.5),(3.6),(3.7) 本质是一样的,(3.6)按列的处理方式方便人脑的思考,而(3.7)按行的处理方式方便电脑的计算。所以,很多行的性质和列的性质都是通用的
矩阵秩的定义 定义1 :在 m × n m \times n m × n A A A k k k k k k ( k ≤ m , k ≤ n ) (k \leq m, k \leq n) ( k ≤ m , k ≤ n ) k 2 k^2 k 2 A A A k k k A A A k k k
定义2 m × n m \times n m × n A A A k k k C m k ⋅ C n k C_m^k \cdot C_n^k C m k ⋅ C n k
定义3 设在矩阵 A A A r r r D 1 D_1 D 1 r + 1 r+1 r + 1 D D D A A A r r r A A A 秩 ,记作 R ( A ) R(A) R ( A )
并规定:零矩阵的秩等于 0.
由行列式按行(列)展开的性质可知,若 A A A r + 1 r+1 r + 1 r + 1 r+1 r + 1 r r r D D D A A A R ( A ) R(\boldsymbol{A}) R ( A ) A \boldsymbol{A} A k k k R ( A ) ≥ k R(\boldsymbol{A}) \geq k R ( A ) ≥ k A \boldsymbol{A} A k k k R ( A ) < k R(\boldsymbol{A})<k R ( A ) < k n n n A A A A A A n n n ∣ A ∣ |\boldsymbol{A}| ∣ A ∣ ∣ A ∣ ≠ 0 |A| \neq 0 ∣ A ∣ = 0 R ( A ) = n R(A)=n R ( A ) = n ∣ A ∣ = 0 |\boldsymbol{A}|=0 ∣ A ∣ = 0 R ( A ) < n R(\boldsymbol{A})<n R ( A ) < n 满秩矩阵 ,不可逆矩阵又称为降秩矩阵 .
矩阵秩的性质 性质 设矩阵 A m × n \boldsymbol{A}_{m \times n} A m × n A \boldsymbol{A} A 0 ⩽ r ( A ) ⩽ min { m , n } 0 \leqslant r(\boldsymbol{A}) \leqslant \min \{m, n\} 0 ⩽ r ( A ) ⩽ min { m , n } A 1 \boldsymbol{A}_1 A 1 A \boldsymbol{A} A r ( A 1 ) ⩽ r ( A ) r\left(\boldsymbol{A}_1\right) \leqslant r(\boldsymbol{A}) r ( A 1 ) ⩽ r ( A ) A \boldsymbol{A} A r r r r ( A ) ⩾ r r(\boldsymbol{A}) \geqslant r r ( A ) ⩾ r A \boldsymbol{A} A r r r r ( A ) < r r(\boldsymbol{A})<r r ( A ) < r r ( A T ) = r ( A ) r\left(\boldsymbol{A}^{\mathrm{T}}\right)=r(\boldsymbol{A}) r ( A T ) = r ( A ) r ( k A ) = { r ( A ) , k ≠ 0 , 0 , k = 0. r(k \boldsymbol{A})=\left\{\begin{array}{cc}r(\boldsymbol{A}), & k \neq 0, \\ 0, & k=0 .\end{array}\right. r ( k A ) = { r ( A ) , 0 , k = 0 , k = 0.
矩阵秩的求法 例 求矩阵A的秩
A = [ 1 1 − 1 4 2 1 3 0 0 1 − 5 8 ] A=\left[\begin{array}{rrrr}
1 & 1 & -1 & 4 \\
2 & 1 & 3 & 0 \\
0 & 1 & -5 & 8
\end{array}\right] A = 1 2 0 1 1 1 − 1 3 − 5 4 0 8 解:将矩阵A化为行的阶梯矩阵有,
A = [ 1 1 − 1 4 2 1 3 0 0 1 − 5 8 ] → [ 1 1 − 1 4 0 − 1 5 − 8 0 1 − 5 8 ] A=\left[\begin{array}{rrrr}
1 & 1 & -1 & 4 \\
2 & 1 & 3 & 0 \\
0 & 1 & -5 & 8
\end{array}\right] \rightarrow\left[\begin{array}{rrrr}
1 & 1 & -1 & 4 \\
0 & -1 & 5 & -8 \\
0 & 1 & -5 & 8
\end{array}\right] A = 1 2 0 1 1 1 − 1 3 − 5 4 0 8 → 1 0 0 1 − 1 1 − 1 5 − 5 4 − 8 8 得
A = [ 1 1 − 1 4 0 1 − 5 8 0 0 0 0 ] A=\left[\begin{array}{rrrr}
1 & 1 & -1 & 4 \\
0 & 1 & -5 & 8 \\
0 & 0 & 0 & 0
\end{array}\right] A = 1 0 0 1 1 0 − 1 − 5 0 4 8 0 因为阶梯一共2层,所以R ( A ) = 2 R(A)=2 R ( A ) = 2
例 设矩阵 A 4 × 3 \boldsymbol{A}_{4 \times 3} A 4 × 3 r ( A ) = 2 , B = ( 1 0 2 0 2 0 − 1 0 3 ) r(\boldsymbol{A})=2, \boldsymbol{B}=\left(\begin{array}{rrr}1 & 0 & 2 \\ 0 & 2 & 0 \\ -1 & 0 & 3\end{array}\right) r ( A ) = 2 , B = 1 0 − 1 0 2 0 2 0 3 r ( A B ) r(\boldsymbol{A} \boldsymbol{B}) r ( A B )
解:因为 ∣ B ∣ = 2 ∣ 1 2 − 1 3 ∣ = 2 × 5 = 10 ≠ 0 |\boldsymbol{B}|=2\left|\begin{array}{rr}1 & 2 \\ -1 & 3\end{array}\right|=2 \times 5=10 \neq 0 ∣ B ∣ = 2 1 − 1 2 3 = 2 × 5 = 10 = 0 B \boldsymbol{B} B r ( A B ) = r ( A ) = 2 r(\boldsymbol{A B})=r(\boldsymbol{A})=2 r ( AB ) = r ( A ) = 2
方程的解 定理1 m × n m \times n m × n A x = b \boldsymbol{A x}=\boldsymbol{b} Ax = b A ~ = \widetilde{\boldsymbol{A}}= A = A b A \quad b A b r ( A ) = r ( A ~ ) r(\boldsymbol{A})=r(\tilde{\boldsymbol{A}}) r ( A ) = r ( A ~ ) r ( A ) = r ( A ~ ) = n r(\boldsymbol{A})=r(\widetilde{\boldsymbol{A}})=n r ( A ) = r ( A ) = n r ( A ) = r ( A ~ ) < n r(\boldsymbol{A})=r(\tilde{\boldsymbol{A}})<n r ( A ) = r ( A ~ ) < n r ( A ) < r ( A ~ ) r(\boldsymbol{A})<r(\tilde{\boldsymbol{A}}) r ( A ) < r ( A ~ )
定理2 m × n m \times n m × n A x = 0 A x=0 A x = 0 r ( A ) = n r(\boldsymbol{A})=n r ( A ) = n r ( A ) < n r(\boldsymbol{A})<n r ( A ) < n m < n m<n m < n m = n m=n m = n ∣ A ∣ ≠ 0 |\boldsymbol{A}| \neq 0 ∣ A ∣ = 0 ∣ A ∣ = 0 |\boldsymbol{A}|=0 ∣ A ∣ = 0
上面得到了如下这个阶梯形矩阵,我们继续化简
[ 1 − 2 − 1 3 1 0 0 1 − 2 1 0 0 0 0 0 ] \left[\begin{array}{rrrr|r}
1 & -2 & -1 & 3 & 1 \\
0 & 0 & 1 & -2 & 1 \\
0 & 0 & 0 & 0 & 0
\end{array}\right] 1 0 0 − 2 0 0 − 1 1 0 3 − 2 0 1 1 0 我们通过把第二行加到第一行来把它化简(只能从下往上运算):
行最简形矩阵 ”
相应的简化方程组为
{ x 1 − 2 x 2 + x 4 = 2 x 3 − 2 x 4 = 1 0 = 0 \left\{
\begin{aligned}
&x_1 -2 x_2 & +x_4 & =2 \\
& & x_3-2 x_4 & =1 \\
& & 0 & =0
\end{aligned}
\right. ⎩ ⎨ ⎧ x 1 − 2 x 2 + x 4 x 3 − 2 x 4 0 = 2 = 1 = 0 首非零元为 1 在第 1 列和第 3 列,所以对应的变量 x 1 x_1 x 1 x 3 x_3 x 3 首变量 (主要的变量),因为矩阵是行最简阶梯形,所以这些方程可以用系数非1变量 x 2 x_2 x 2 x 4 x_4 x 4 x 2 , x 4 x_2, ~ x_4 x 2 , x 4 自由变量 。更准确地说,在这个例子中,我们设 x 2 = C 1 x_2= C_1 x 2 = C 1 x 4 = C 2 x_4= C_2 x 4 = C 2 C 1 C_1 C 1 C 2 C_2 C 2
{ x 1 − 2 C 1 + C 2 = 2 x 3 − 2 C 2 = 1 \left\{
\begin{array}{r}
x_1-2 C_1+C_2=2 \\
x_3-2 C_2=1
\end{array}
\right. { x 1 − 2 C 1 + C 2 = 2 x 3 − 2 C 2 = 1 最后方程组的解用参数,用 C 1 , C 2 C_1,C_2 C 1 , C 2
{ x 1 = 2 + 2 C 1 − C 2 x 2 = C 1 x 3 = 1 + 2 C 2 x 4 = C 2 \left\{
\begin{aligned}
& x_1=2+2 C_1-C_2 \\
& x_2=C_1 \\
& x_3=1+2 C_2 \\
& x_4=C_2
\end{aligned}
\right. ⎩ ⎨ ⎧ x 1 = 2 + 2 C 1 − C 2 x 2 = C 1 x 3 = 1 + 2 C 2 x 4 = C 2 由于 C 1 , C 2 C_1, C_2 C 1 , C 2
解线性方程组 对于 n n n { a 1 x 1 + a 2 x 2 + ⋯ + a 1 x 1 x 1 = b 1 , a 2 a 1 a 2 + ⋯ + ⋯ + a 2 x n = b 2 , a m x 1 + a m 2 x 2 + ⋯ + a m , x n = b m , \left\{\begin{array}{l}a_1 x_1+a_2 x_2+\cdots+a_1 x_1 x_1=b_1, \\ a_2 a_1 a_2+\cdots+\cdots+a_2 x_n=b_2, \\ a_m x_1+a_{m 2} x_2+\cdots+a_{m, x_n}=b_m,\end{array}\right. ⎩ ⎨ ⎧ a 1 x 1 + a 2 x 2 + ⋯ + a 1 x 1 x 1 = b 1 , a 2 a 1 a 2 + ⋯ + ⋯ + a 2 x n = b 2 , a m x 1 + a m 2 x 2 + ⋯ + a m , x n = b m ,
如果 b i ( i = 1 , 2 , ⋯ , m ) b_i(i=1,2, \cdots, m) b i ( i = 1 , 2 , ⋯ , m ) n n n 齐次线性方程组 .
如果 b i ( i = 1 , 2 , ⋯ , m ) b_i(i=1,2, \cdots, m) b i ( i = 1 , 2 , ⋯ , m ) n n n 非齐次线性方程组 .
显然,齐次线性方程组一定有解 x 1 = x 2 = ⋯ = x n = 0 x_1=x_2=\cdots=x_n=0 x 1 = x 2 = ⋯ = x n = 0
对于方程组系数组成的矩阵称为方程的系数矩阵 ,如果矩阵包含右边常数项,则成为方程的增广矩阵
解方程的步骤 解n n n
{ a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n = b 2 ⋯ + ⋯ a m 1 x 1 + a m 2 x 2 + ⋯ + a m n x n = b m \left\{\begin{array}{c}
a_{11} x_1+a_{12} x_2+\cdots+a_{1 n} x_n=b_1 \\
a_{21} x_1+a_{22} x_2+\cdots+a_{2 n} x_n=b_2 \\
\cdots+\cdots \\
a_{m 1} x_1+a_{m 2} x_2+\cdots+a_{m n} x_n=b_m
\end{array}\right. ⎩ ⎨ ⎧ a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n = b 2 ⋯ + ⋯ a m 1 x 1 + a m 2 x 2 + ⋯ + a mn x n = b m 的具体步骤为
01写出线性方程组的增广矩阵 A ~ \tilde{A} A ~ A ~ \tilde{A} A ~ R ~ \tilde{R} R ~ R ~ \tilde{R} R ~
例解方程组
{ x 1 − x 2 + 2 x 3 − 2 x 4 = 1 , x 2 + x 3 + 2 x 4 = − 1 , 2 x 1 − x 2 + 5 x 3 − 2 x 4 = 1 x 1 − x 2 − 4 x 4 = 3. \left\{\begin{array}{r}
x_1-x_2+2 x_3-2 x_4=1, \\
x_2+x_3+2 x_4=-1, \\
2 x_1-x_2+5 x_3-2 x_4=1 \\
x_1-x_2-4 x_4=3 .
\end{array}\right. ⎩ ⎨ ⎧ x 1 − x 2 + 2 x 3 − 2 x 4 = 1 , x 2 + x 3 + 2 x 4 = − 1 , 2 x 1 − x 2 + 5 x 3 − 2 x 4 = 1 x 1 − x 2 − 4 x 4 = 3. 对该线性方程组的增广矩阵实施初等行变换,
A ~ = ( 1 − 1 2 − 2 1 0 1 1 2 − 1 2 − 1 5 − 2 1 1 − 1 0 − 4 3 ) ⟶ r 4 + ( − 1 ) r 1 r 3 + ( − 2 ) 1 ( 1 − 1 2 − 2 1 0 1 1 2 − 1 0 1 1 2 − 1 0 0 − 2 − 2 2 ) ⟶ − 1 2 r 4 r 3 + ( − 1 ) r 2 ( 1 − 1 2 − 2 1 0 1 1 2 − 1 0 0 0 0 0 0 0 1 1 − 1 ) \tilde{\boldsymbol{A}}=\left(\begin{array}{ccccc}
1 & -1 & 2 & -2 & 1 \\
0 & 1 & 1 & 2 & -1 \\
2 & -1 & 5 & -2 & 1 \\
1 & -1 & 0 & -4 & 3
\end{array}\right) \stackrel{r_3+(-2)_1}{\stackrel{r_4+(-1) r_1}{\longrightarrow}}\left(\begin{array}{ccccc}
1 & -1 & 2 & -2 & 1 \\
0 & 1 & 1 & 2 & -1 \\
0 & 1 & 1 & 2 & -1 \\
0 & 0 & -2 & -2 & 2
\end{array}\right) \stackrel{ r_3+(-1) r_2} {\stackrel{ -\frac{1}{2} r_4 }{\longrightarrow}}\left(\begin{array}{ccccc}
1 & -1 & 2 & -2 & 1 \\
0 & 1 & 1 & 2 & -1 \\
0 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 1 & -1
\end{array}\right) A ~ = 1 0 2 1 − 1 1 − 1 − 1 2 1 5 0 − 2 2 − 2 − 4 1 − 1 1 3 ⟶ r 4 + ( − 1 ) r 1 r 3 + ( − 2 ) 1 1 0 0 0 − 1 1 1 0 2 1 1 − 2 − 2 2 2 − 2 1 − 1 − 1 2 ⟶ − 2 1 r 4 r 3 + ( − 1 ) r 2 1 0 0 0 − 1 1 0 0 2 1 0 1 − 2 2 0 1 1 − 1 0 − 1 ⟶ r 3 ↔ r 4 ( 1 − 1 2 − 2 1 0 1 1 2 − 1 0 0 1 1 − 1 0 0 0 0 0 ) ⟶ r 2 + ( − 1 ) r 3 ( 1 − 1 0 − 4 3 0 1 0 1 0 0 0 1 1 − 1 0 0 0 0 0 ) ⟶ r 1 + ( − 2 ) r 3 ( 1 0 0 − 3 3 0 1 0 1 0 0 0 1 1 − 1 0 0 0 0 0 ) \stackrel{r_3 \leftrightarrow r_4}{\longrightarrow}\left(\begin{array}{ccccc}
1 & -1 & 2 & -2 & 1 \\
0 & 1 & 1 & 2 & -1 \\
0 & 0 & 1 & 1 & -1 \\
0 & 0 & 0 & 0 & 0
\end{array}\right) \stackrel{r_2+(-1)_{r_3}}{\longrightarrow}\left(\begin{array}{ccccc}
1 & -1 & 0 & -4 & 3 \\
0 & 1 & 0 & 1 & 0 \\
0 & 0 & 1 & 1 & -1 \\
0 & 0 & 0 & 0 & 0
\end{array}\right) \stackrel{r_1+(-2) r_3}{\longrightarrow}\left(\begin{array}{ccccc}
1 & 0 & 0 & -3 & 3 \\
0 & 1 & 0 & 1 & 0 \\
0 & 0 & 1 & 1 & -1 \\
0 & 0 & 0 & 0 & 0
\end{array}\right) ⟶ r 3 ↔ r 4 1 0 0 0 − 1 1 0 0 2 1 1 0 − 2 2 1 0 1 − 1 − 1 0 ⟶ r 2 + ( − 1 ) r 3 1 0 0 0 − 1 1 0 0 0 0 1 0 − 4 1 1 0 3 0 − 1 0 ⟶ r 1 + ( − 2 ) r 3 1 0 0 0 0 1 0 0 0 0 1 0 − 3 1 1 0 3 0 − 1 0 从而原方程组等价于 { x 1 − 3 x 4 = 3 , x 2 + x 4 = 0 , x 3 + x 4 = − 1 , 0 = 0. \left\{\begin{array}{cr}x_1 & -3 x_4=3, \\ & x_2 \\ & +x_4=0, \\ & x_3+x_4=-1, \\ & 0=0 .\end{array}\right. ⎩ ⎨ ⎧ x 1 − 3 x 4 = 3 , x 2 + x 4 = 0 , x 3 + x 4 = − 1 , 0 = 0. x 4 = c x_4=c x 4 = c { x 1 = 3 + 3 c , x 2 = − c , x 3 = − 1 − c , x 4 = c \left\{\begin{array}{l}x_1=3+3 c, \\ x_2=-c, \\ x_3=-1-c, \\ x_4=c\end{array}\right. ⎩ ⎨ ⎧ x 1 = 3 + 3 c , x 2 = − c , x 3 = − 1 − c , x 4 = c c c c
例解方程组
{ x 1 + x 2 − 2 x 3 = 1 , 3 x 1 + 8 x 2 + x 3 = − 2 , 7 x 1 + 2 x 2 − 21 x 3 = 13. \left\{\begin{array}{l}
x_1+x_2-2 x_3=1, \\
3 x_1+8 x_2+x_3=-2, \\
7 x_1+2 x_2-21 x_3=13 .
\end{array}\right. ⎩ ⎨ ⎧ x 1 + x 2 − 2 x 3 = 1 , 3 x 1 + 8 x 2 + x 3 = − 2 , 7 x 1 + 2 x 2 − 21 x 3 = 13. 解:对方程进行增广矩阵变换得到
A ~ = ( 1 1 − 2 1 3 8 1 − 2 7 2 − 21 13 ) → r 3 + ( − 7 ) r 1 r 2 + ( − 3 ) r 1 ( 1 1 − 2 1 0 5 7 − 5 0 − 5 − 7 6 ) → r 3 + r 2 ( 1 1 − 2 1 0 5 7 − 5 0 0 0 1 ) , \tilde{\boldsymbol{A}}=\left(\begin{array}{cccc}
1 & 1 & -2 & 1 \\
3 & 8 & 1 & -2 \\
7 & 2 & -21 & 13
\end{array}\right) \xrightarrow[r_3+(-7) r_1]{r_2+(-3) r_1}\left(\begin{array}{cccc}
1 & 1 & -2 & 1 \\
0 & 5 & 7 & -5 \\
0 & -5 & -7 & 6
\end{array}\right) \xrightarrow{r_3+r_2}\left(\begin{array}{cccc}
1 & 1 & -2 & 1 \\
0 & 5 & 7 & -5 \\
0 & 0 & 0 & 1
\end{array}\right), A ~ = 1 3 7 1 8 2 − 2 1 − 21 1 − 2 13 r 2 + ( − 3 ) r 1 r 3 + ( − 7 ) r 1 1 0 0 1 5 − 5 − 2 7 − 7 1 − 5 6 r 3 + r 2 1 0 0 1 5 0 − 2 7 0 1 − 5 1 , 从而原方程等价于
= { x 1 + x 2 − 2 x 3 = 1 5 x 2 + 7 x 3 = − 5 0 = 1 =\left\{\begin{aligned}
x_1+x_2-2 x_3 & =1 \\
5 x_2+7 x_3 & =-5 \\
0 & =1
\end{aligned}\right. = ⎩ ⎨ ⎧ x 1 + x 2 − 2 x 3 5 x 2 + 7 x 3 0 = 1 = − 5 = 1 最后一个方程矛盾,所以原方程无解。
例 解线性方程组 { 3 x 1 + 2 x 2 + 5 x 3 = 0 , 3 x 1 − 2 x 2 + 6 x 3 = 0 , 2 x 1 + 5 x 3 = 0. \left\{\begin{array}{r}3 x_1+2 x_2+5 x_3=0, \\ 3 x_1-2 x_2+6 x_3=0, \\ 2 x_1+5 x_3=0 .\end{array}\right. ⎩ ⎨ ⎧ 3 x 1 + 2 x 2 + 5 x 3 = 0 , 3 x 1 − 2 x 2 + 6 x 3 = 0 , 2 x 1 + 5 x 3 = 0.
解 对该线性方程组的系数矩阵实施初等行变换,得:
( 3 2 5 3 − 2 6 2 0 5 ) → r 1 ↔ r 3 ( 2 0 5 3 − 2 6 3 2 5 ) → r 3 + ( − 1 ) r 2 1 2 r 1 ( 1 0 5 2 3 − 2 6 0 4 − 1 ) → r 2 + ( − 3 ) r 1 ( 1 0 5 2 0 − 2 − 3 2 0 4 − 1 ) \left(\begin{array}{ccc}
3 & 2 & 5 \\
3 & -2 & 6 \\
2 & 0 & 5
\end{array}\right) \xrightarrow{r_1 \leftrightarrow r_3}\left(\begin{array}{ccc}
2 & 0 & 5 \\
3 & -2 & 6 \\
3 & 2 & 5
\end{array}\right) \xrightarrow[r_3+(-1) r_2]{\frac{1}{2} r_1}\left(\begin{array}{ccc}
1 & 0 & \frac{5}{2} \\
3 & -2 & 6 \\
0 & 4 & -1
\end{array}\right) \xrightarrow{r_2+(-3) r_1}\left(\begin{array}{ccc}
1 & 0 & \frac{5}{2} \\
0 & -2 & -\frac{3}{2} \\
0 & 4 & -1
\end{array}\right) 3 3 2 2 − 2 0 5 6 5 r 1 ↔ r 3 2 3 3 0 − 2 2 5 6 5 2 1 r 1 r 3 + ( − 1 ) r 2 1 3 0 0 − 2 4 2 5 6 − 1 r 2 + ( − 3 ) r 1 1 0 0 0 − 2 4 2 5 − 2 3 − 1 → r 3 + 2 r 2 ( 1 0 5 2 0 − 2 − 3 2 0 0 − 4 ) → r 1 + 5 8 r 3 r 2 + ( − 3 8 ) r 3 ( 1 0 0 0 − 2 0 0 0 − 4 ) → ( − 1 4 ) r 3 ( − 1 2 ) r 2 ( 1 0 0 0 1 0 0 0 1 ) , \xrightarrow{r_3+2 r_2}\left(\begin{array}{ccc}
1 & 0 & \frac{5}{2} \\
0 & -2 & -\frac{3}{2} \\
0 & 0 & -4
\end{array}\right) \xrightarrow[\substack{r_1+\frac{5}{8} r_3 \\
r_2+\left(-\frac{3}{8}\right) r_3}]{ }\left(\begin{array}{ccc}
1 & 0 & 0 \\
0 & -2 & 0 \\
0 & 0 & -4
\end{array}\right) \xrightarrow[\left(-\frac{1}{4}\right) r_3]{\left(-\frac{1}{2}\right) r_2}\left(\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right), r 3 + 2 r 2 1 0 0 0 − 2 0 2 5 − 2 3 − 4 r 1 + 8 5 r 3 r 2 + ( − 8 3 ) r 3 1 0 0 0 − 2 0 0 0 − 4 ( − 2 1 ) r 2 ( − 4 1 ) r 3 1 0 0 0 1 0 0 0 1 , 所以方程组只有零解。
例 解方程组
{ x 1 + x 2 − 2 x 3 + x 4 = 0 2 x 1 − x 2 − x 3 + x 4 = 0 3 x 1 + 6 x 2 − 9 x 3 + 7 x 4 = 0 4 x 1 − 6 x 2 + 2 x 3 − 2 x 4 = 0 \left\{\begin{array}{r}
x_1+x_2-2 x_3+x_4=0 \\
2 x_1-x_2-x_3+x_4=0 \\
3 x_1+6 x_2-9 x_3+7 x_4=0 \\
4 x_1-6 x_2+2 x_3-2 x_4=0
\end{array}\right. ⎩ ⎨ ⎧ x 1 + x 2 − 2 x 3 + x 4 = 0 2 x 1 − x 2 − x 3 + x 4 = 0 3 x 1 + 6 x 2 − 9 x 3 + 7 x 4 = 0 4 x 1 − 6 x 2 + 2 x 3 − 2 x 4 = 0 解 对该线性方程组的系数矩阵实施初等行变换,得:
( 1 1 − 2 1 2 − 1 − 1 1 3 6 − 9 7 4 − 6 2 − 2 ) → r 4 + ( − 4 ) r 1 r 2 + ( − 2 ) r 1 r 2 + ( − 2 ) r 4 ( 1 1 − 2 1 0 − 3 3 − 1 0 3 − 3 4 0 − 10 10 − 6 ) \left(\begin{array}{cccc}
1 & 1 & -2 & 1 \\
2 & -1 & -1 & 1 \\
3 & 6 & -9 & 7 \\
4 & -6 & 2 & -2
\end{array}\right) \xrightarrow[\substack{r_4+(-4) r_1 \\
r_2+(-2) r_1}]{\substack{r_2+(-2) \\
r_4}}\left(\begin{array}{cccc}
1 & 1 & -2 & 1 \\
0 & -3 & 3 & -1 \\
0 & 3 & -3 & 4 \\
0 & -10 & 10 & -6
\end{array}\right) 1 2 3 4 1 − 1 6 − 6 − 2 − 1 − 9 2 1 1 7 − 2 r 2 + ( − 2 ) r 4 r 4 + ( − 4 ) r 1 r 2 + ( − 2 ) r 1 1 0 0 0 1 − 3 3 − 10 − 2 3 − 3 10 1 − 1 4 − 6 ( 1 1 − 2 1 0 − 3 3 − 1 0 0 0 3 0 − 10 10 − 6 ) → 3 3 1 3 r 4 + 2 r 3 ( 1 1 − 2 1 0 − 3 3 − 1 0 0 0 1 0 − 10 10 0 ) \left(\begin{array}{cccc}
1 & 1 & -2 & 1 \\
0 & -3 & 3 & -1 \\
0 & 0 & 0 & 3 \\
0 & -10 & 10 & -6
\end{array}\right) \xrightarrow[\frac{3}{3}^{\frac{1}{3}}]{r_4+2 r_3}\left(\begin{array}{cccc}
1 & 1 & -2 & 1 \\
0 & -3 & 3 & -1 \\
0 & 0 & 0 & 1 \\
0 & -10 & 10 & 0
\end{array}\right) 1 0 0 0 1 − 3 0 − 10 − 2 3 0 10 1 − 1 3 − 6 r 4 + 2 r 3 3 3 3 1 1 0 0 0 1 − 3 0 − 10 − 2 3 0 10 1 − 1 1 0 ( 1 1 − 2 0 0 1 − 1 0 0 0 0 1 0 0 0 0 ) → r 1 + ( − 1 ) r 2 ( 1 0 − 1 0 0 1 − 1 0 0 0 0 1 0 0 0 0 ) \left(\begin{array}{cccc}
1 & 1 & -2 & 0 \\
0 & 1 & -1 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0
\end{array}\right) \xrightarrow{r_1+(-1) r_2}\left(\begin{array}{cccc}
1 & 0 & -1 & 0 \\
0 & 1 & -1 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0
\end{array}\right) 1 0 0 0 1 1 0 0 − 2 − 1 0 0 0 0 1 0 r 1 + ( − 1 ) r 2 1 0 0 0 0 1 0 0 − 1 − 1 0 0 0 0 1 0 从而原方程组等价于 { x 1 − x 3 = 0 , x 2 − x 3 = 0 , x 4 = 0. \left\{\begin{array}{l}x_1-x_3=0, \\ x_2-x_3=0, \\ x_4=0 .\end{array}\right. ⎩ ⎨ ⎧ x 1 − x 3 = 0 , x 2 − x 3 = 0 , x 4 = 0. x 3 = c x_3=c x 3 = c { x 1 = c , x 2 = c , x 3 = c , x 4 = 0. \left\{\begin{array}{l}x_1=c, \\ x_2=c, \\ x_3=c, \\ x_4=0 .\end{array}\right. ⎩ ⎨ ⎧ x 1 = c , x 2 = c , x 3 = c , x 4 = 0. c c c
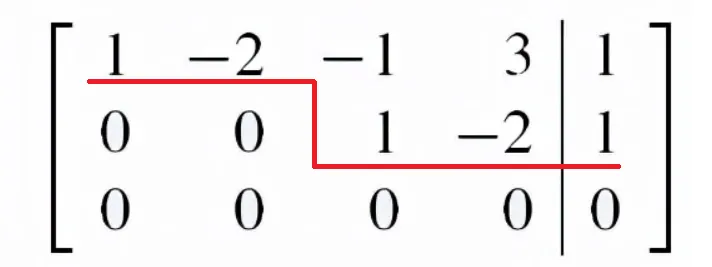 {width=300px}
{width=300px}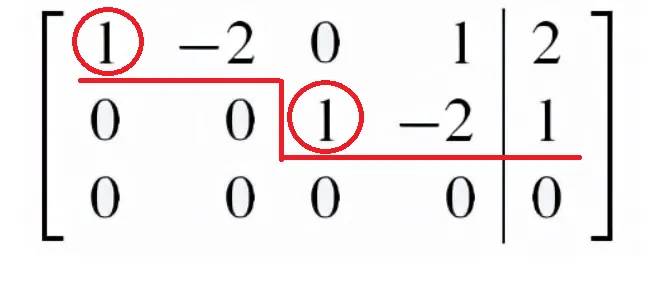 {width=300px}
这样就化为“行最简形矩阵”
{width=300px}
这样就化为“行最简形矩阵”