33._矩阵的QR分解

矩阵的QR分解

重要说明：本文设计到施密特正交化，点击查看施密特正交化，本文主要有AI生成

1. 核心思想与定义

QR分解 将一个矩阵 $A$ 分解为一个正交矩阵（Orthogonal matrix）和一个上三角矩阵（Upper triangular matrix）的乘积：

A = QR

其中：

$Q$ 是一个正交矩阵（若 $A$ 为实矩阵），即满足 $Q^T Q = I$ 。其列向量构成一组标准正交基。
$R$ 是一个上三角矩阵。

维度说明：

若 $A$ 是 $m \times n$ 的满列秩矩阵（即 $\text{rank}(A) = n$ ），则：
$Q$ 是 $m \times n$ 的矩阵，其列正交。
$R$ 是 $n \times n$ 的上三角可逆矩阵。
若 $A$ 的列秩亏损，分解仍然存在，但形式略有不同（通常称为瘦QR分解（Thin QR Factorization））。

2. 为什么需要QR分解？

QR分解的核心价值在于将任意矩阵的列向量转换为一组正交的向量。这带来了许多优势：

数值稳定性：正交变换（如Householder反射）不会放大误差，使得QR分解在数值计算中非常可靠。
求解最小二乘问题：这是QR分解最重要的应用。对于超定方程组 $A \mathbf{x} = \mathbf{b}$ （无精确解），通过QR分解将其转化为 $R \mathbf{x} = Q^T \mathbf{b}$ 。由于 $R$ 是上三角矩阵，该方程可以高效、稳定地求解，得到最小二乘解。
计算特征值：著名的QR算法用于计算矩阵的所有特征值，它迭代地应用QR分解。
正交化：QR分解提供了一种为矩阵 $A$ 的列空间构建一组标准正交基的方法。

3. 分解方法

主要有两种算法来计算QR分解：Gram-Schmidt正交化过程 和 Householder变换。

方法一：Gram-Schmidt正交化过程

这是最直观的方法，直接对 $A$ 的列向量进行正交化。

步骤：设 $A = [\mathbf{a}_1, \mathbf{a}_2, ..., \mathbf{a}_n]$ ，我们的目标是找到一组标准正交向量 $\{\mathbf{q}_1, \mathbf{q}_2, ..., \mathbf{q}_n\}$ 使得：

\begin{aligned} \text{span}\{\mathbf{a}_1, ..., \mathbf{a}_k\} &= \text{span}\{\mathbf{q}_1, ..., \mathbf{q}_k\}, \quad \text{for } k=1,...,n \\ \mathbf{a}_k &= r_{1k}\mathbf{q}_1 + r_{2k}\mathbf{q}_2 + ... + r_{kk}\mathbf{q}_k \end{aligned}

第一步：

\begin{aligned} \mathbf{u}_1 &= \mathbf{a}_1 \\ \mathbf{q}_1 &= \frac{\mathbf{u}_1}{\|\mathbf{u}_1\|} \\ r_{11} &= \|\mathbf{u}_1\| \end{aligned}

第 $k$ 步（ $k = 2, ..., n$ )**：

\begin{aligned} \mathbf{u}_k &= \mathbf{a}_k - (\mathbf{q}_1^T \mathbf{a}_k)\mathbf{q}_1 - (\mathbf{q}_2^T \mathbf{a}_k)\mathbf{q}_2 - ... - (\mathbf{q}_{k-1}^T \mathbf{a}_k)\mathbf{q}_{k-1} \\ \mathbf{q}_k &= \frac{\mathbf{u}_k}{\|\mathbf{u}_k\|} \\ r_{jk} &= \mathbf{q}_j^T \mathbf{a}_k \quad \text{for } j = 1, ..., k-1 \\ r_{kk} &= \|\mathbf{u}_k\| \end{aligned}

构造 $Q$ 和 $R$ ：

$Q = [\mathbf{q}_1, \mathbf{q}_2, ..., \mathbf{q}_n]$
$R$ 是一个上三角矩阵，其元素 $r_{ij}$ 由上述过程定义：

R = \begin{bmatrix} r_{11} & r_{12} & \cdots & r_{1n} \\ 0 & r_{22} & \cdots & r_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & r_{nn} \end{bmatrix}

缺点：经典Gram-Schmidt过程在数值计算中可能不稳定（正交性会因舍入误差而丢失）。通常使用改进的Gram-Schmidt过程。

方法二：Householder变换（更常用、更稳定）

Householder变换通过一系列的反射操作，逐步将矩阵 $A$ 的上三角部分以下的元素变为零。

思想：找到一个正交矩阵 $H$ ，使得 $H \mathbf{x} = \alpha \mathbf{e}_1$ （其中 $\mathbf{e}_1$ 是第一个标准基向量）。这个矩阵 $H$ 就是Householder反射矩阵。

步骤：对于 $k = 1$ to $n$ ：

考虑 $A$ 的第 $k$ 列的对角线以下部分 $\mathbf{x} = A[k:m, k]$ 。
计算一个Householder向量 $\mathbf{v}_k$ 和一个标量 $\beta_k$ ，使得应用反射 $H_k = I - \beta_k \mathbf{v}_k \mathbf{v}_k^T$ 后，能将 $\mathbf{x}$ 除第一个元素外的所有元素变为零。
将反射应用到 $A$ 的右下子矩阵上： $A[k:m, k:n] = H_k \cdot A[k:m, k:n]$ 。
同时，记录这些变换（如果需要显式生成 $Q$ ）。

所有变换完成后，原来的 $A$ 就被变换成了上三角矩阵 $R$ 。

H_n H_{n-1} \cdots H_1 A = R \implies A = (H_1 H_2 \cdots H_n) R

因为Householder反射是对称且正交的（ $H^T = H$ , $H^T H = I$ ），所以所有反射的乘积 $Q^T = H_n \cdots H_1$ 也是一个正交矩阵，因此 $Q = H_1 \cdots H_n$ ，最终得到 $A = QR$ 。

优点：数值稳定性远高于Gram-Schmidt方法，是数值计算软件（如MATLAB, NumPy）中 qr() 函数使用的标准算法。

4. 例子（Gram-Schmidt过程）

设矩阵 $A = \begin{bmatrix} 1 & 1 \\ 2 & 0 \\ 0 & 1 \end{bmatrix}$ ，求其QR分解。

Step 1: 处理第一列 $\mathbf{a}_1$

\begin{aligned} \mathbf{u}_1 &= \mathbf{a}_1 = \begin{bmatrix} 1 \\ 2 \\ 0 \end{bmatrix} \\ \|\mathbf{u}_1\| &= \sqrt{1^2 + 2^2 + 0^2} = \sqrt{5} \\ \mathbf{q}_1 &= \frac{\mathbf{u}_1}{\|\mathbf{u}_1\|} = \begin{bmatrix} 1/\sqrt{5} \\ 2/\sqrt{5} \\ 0 \end{bmatrix} \\ r_{11} &= \|\mathbf{u}_1\| = \sqrt{5} \end{aligned}

Step 2: 处理第二列 $\mathbf{a}_2$ 先减去它在 $\mathbf{q}_1$ 上的投影：

\begin{aligned} r_{12} &= \mathbf{q}_1^T \mathbf{a}_2 = \begin{bmatrix} 1/\sqrt{5} & 2/\sqrt{5} & 0 \end{bmatrix} \begin{bmatrix} 1 \\ 0 \\ 1 \end{bmatrix} = \frac{1}{\sqrt{5}} \\ \mathbf{u}_2 &= \mathbf{a}_2 - r_{12} \mathbf{q}_1 = \begin{bmatrix} 1 \\ 0 \\ 1 \end{bmatrix} - \frac{1}{\sqrt{5}} \begin{bmatrix} 1/\sqrt{5} \\ 2/\sqrt{5} \\ 0 \end{bmatrix} = \begin{bmatrix} 1 \\ 0 \\ 1 \end{bmatrix} - \begin{bmatrix} 1/5 \\ 2/5 \\ 0 \end{bmatrix} = \begin{bmatrix} 4/5 \\ -2/5 \\ 1 \end{bmatrix} \\ \|\mathbf{u}_2\| &= \sqrt{(4/5)^2 + (-2/5)^2 + 1^2} = \sqrt{16/25 + 4/25 + 25/25} = \sqrt{45/25} = \frac{3\sqrt{5}}{5} \\ \mathbf{q}_2 &= \frac{\mathbf{u}_2}{\|\mathbf{u}_2\|} = \frac{5}{3\sqrt{5}} \begin{bmatrix} 4/5 \\ -2/5 \\ 1 \end{bmatrix} = \begin{bmatrix} 4/(3\sqrt{5}) \\ -2/(3\sqrt{5}) \\ 5/(3\sqrt{5}) \end{bmatrix} = \begin{bmatrix} 4/(3\sqrt{5}) \\ -2/(3\sqrt{5}) \\ \sqrt{5}/3 \end{bmatrix} \\ r_{22} &= \|\mathbf{u}_2\| = \frac{3\sqrt{5}}{5} \end{aligned}

Step 3: 构造 $Q$ 和 $R$

Q = [\mathbf{q}_1, \mathbf{q}_2] = \begin{bmatrix} 1/\sqrt{5} & 4/(3\sqrt{5}) \\ 2/\sqrt{5} & -2/(3\sqrt{5}) \\ 0 & \sqrt{5}/3 \end{bmatrix}, \quad R = \begin{bmatrix} r_{11} & r_{12} \\ 0 & r_{22} \end{bmatrix} = \begin{bmatrix} \sqrt{5} & 1/\sqrt{5} \\ 0 & 3\sqrt{5}/5 \end{bmatrix}

验证：计算 $QR$ ，结果应等于 $A$ 。（验证略）

5. 总结与对比

特性	QR分解
形式	$A = QR$
矩阵Q	正交矩阵（ $Q^TQ = I$ ），其列是标准正交基。
矩阵R	上三角矩阵。
核心思想	将矩阵的列向量转换为正交的向量。
主要方法	Gram-Schmidt过程、Householder变换、Givens旋转。
最大优点	数值稳定性好（尤其Householder方法）。
主要应用	求解最小二乘问题、计算特征值（QR算法）、信号处理、模式识别。

简单来说，QR分解为我们提供了一种为矩阵的列空间寻找一组‘好’的（即正交的）基的方法。这种性质使得它在解决数值计算问题时非常强大和可靠。

$A=Q R$ 分解图解

$A=Q R$ 是在保持 $\boldsymbol{C}(A)=\boldsymbol{C}(Q)$ 的条件下，将 $A$ 转化为正交矩阵 $Q$ ．在格拉姆－施密特正交化中，首先，单位化的 $\boldsymbol{a}_1$ 被用作 $\boldsymbol{q}_1$ ，然后求出 $\boldsymbol{a}_2$ 与 $\boldsymbol{q}_1$ 正交所得到的 $\boldsymbol{q}_2$ ，以此类推．

\begin{aligned} & \boldsymbol{q}_1=\boldsymbol{a}_1 /\left\|\boldsymbol{a}_1\right\| \\ & \boldsymbol{q}_2=\boldsymbol{a}_2-\left(\boldsymbol{q}_1^{\mathrm{T}} \boldsymbol{a}_2\right) \boldsymbol{q}_1, \quad \boldsymbol{q}_2=\boldsymbol{q}_2 /\left\|\boldsymbol{q}_2\right\| \\ & \boldsymbol{q}_3=\boldsymbol{a}_3-\left(\boldsymbol{q}_1^{\mathrm{T}} \boldsymbol{a}_3\right) \boldsymbol{q}_1-\left(\boldsymbol{q}_2^{\mathrm{T}} \boldsymbol{a}_3\right) \boldsymbol{q}_2, \quad \boldsymbol{q}_3=\boldsymbol{q}_3 /\left\|\boldsymbol{q}_3\right\| \end{aligned}

或者你也可以写作 $r_{i j}=\boldsymbol{q}_i^{\mathrm{T}} \boldsymbol{a}_j$ ：

\begin{aligned} & \boldsymbol{a}_1=r_{11} \boldsymbol{q}_1 \\ & \boldsymbol{a}_2=r_{12} \boldsymbol{q}_1+r_{22} \boldsymbol{q}_2 \\ & \boldsymbol{a}_3=r_{13} \boldsymbol{q}_1+r_{23} \boldsymbol{q}_2+r_{33} \boldsymbol{q}_3 \end{aligned}

原本的 $A$ 就可以表示为 $Q R$ ：正交矩阵乘以上三角矩阵．

$图片$

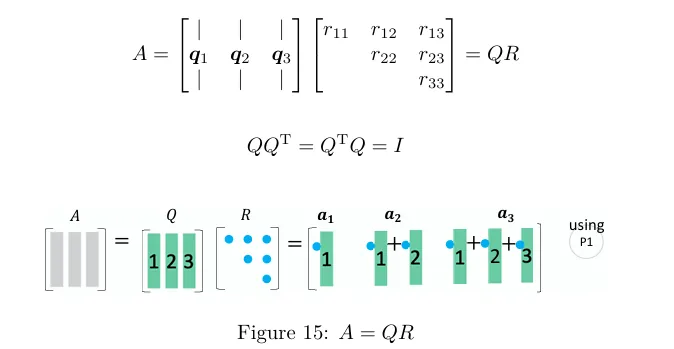
$A$ 的列向量就可以转化为一个正交集合： $Q$ 的列向量． $A$ 的每一个列向量都可以用 $Q$ 和上三角矩阵 $R$ 重新构造出．图释可以回头看 P1．