32._矩阵的CR分解

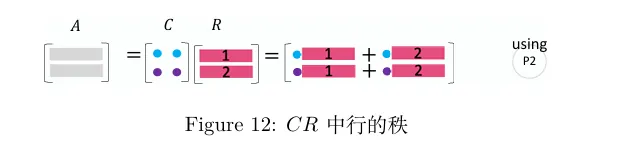
矩阵的CR分解

本文主要由AI生产，请读者自己识别里面内容

1. 核心思想与定义

CR分解 将一个矩阵 AA 分解为两个矩阵的乘积：

A=CRA = C R

其中：

  • CC 是一个由 AA 的 线性无关列（Linear Independent Columns）组成的矩阵。

  • RR 是一个由 AA 的 行最简形（Row Reduced Echelon Form, RREF）的前 rr 行（即非零行）组成的矩阵。

关键点：

  • 设 AA 是一个 m×nm \times n 的矩阵，其秩（Rank）为 rr（即 rank(A)=r\text{rank}(A) = r)。

  • 则 CC 是 m×rm \times r 的矩阵。

  • RR 是 r×nr \times n 的矩阵。

  • 分解后的乘积 CRCR 的秩也为 rr，完美保留了原矩阵的秩。

2. 分解的步骤

通过一个具体例子来演示是最清晰的。设矩阵：

A=[123124621343]A = \begin{bmatrix} 1 & 2 & 3 & 1 \\ 2 & 4 & 6 & 2 \\ 1 & 3 & 4 & 3 \end{bmatrix}

Step 1: 求矩阵 AA 的秩并确定主元列

  1. 对 AA 进行行化简，得到其行最简形（RREF）。

RREF(A)=[1205001−20000]\text{RREF}(A) = \begin{bmatrix} \boxed{1} & 2 & 0 & 5 \\ 0 & 0 & \boxed{1} & -2 \\ 0 & 0 & 0 & 0 \end{bmatrix}

（□ 框出的为主元） 2. 秩 rr 就是主元的个数。这里 r=2r = 2。 3. 主元所在的列号（第1列和第3列）指示了原矩阵 AA 中哪些列是线性无关的。

Step 2: 构造矩阵 CC

  • CC 由 AA 的主元列（Pivot Columns）组成。即第1列和第3列。

C=[132614]C = \begin{bmatrix} 1 & 3 \\ 2 & 6 \\ 1 & 4 \end{bmatrix}

  • CC 的列空间 Col(C)\text{Col}(C) 就等于 AA 的列空间 Col(A)\text{Col}(A)。所有其他的列都是这些主元列的线性组合。

Step 3: 构造矩阵 RR

  • RR 就是 AA 的行最简形（RREF）中的非零行。

R=[1205001−2]R = \begin{bmatrix} 1 & 2 & 0 & 5 \\ 0 & 0 & 1 & -2 \end{bmatrix}

  • RR 的行空间 Row(R)\text{Row}(R) 就等于 AA 的行空间 Row(A)\text{Row}(A)。

Step 4: 验证分解

CR=[132614][1205001−2]=[1⋅1+3⋅01⋅2+3⋅01⋅0+3⋅11⋅5+3⋅(−2)2⋅1+6⋅02⋅2+6⋅02⋅0+6⋅12⋅5+6⋅(−2)1⋅1+4⋅01⋅2+4⋅01⋅0+4⋅11⋅5+4⋅(−2)]=[123−1246−2124−3]C R = \begin{bmatrix} 1 & 3 \\ 2 & 6 \\ 1 & 4 \end{bmatrix} \begin{bmatrix} 1 & 2 & 0 & 5 \\ 0 & 0 & 1 & -2 \end{bmatrix} = \begin{bmatrix} 1\cdot1+3\cdot0 & 1\cdot2+3\cdot0 & 1\cdot0+3\cdot1 & 1\cdot5+3\cdot(-2) \\ 2\cdot1+6\cdot0 & 2\cdot2+6\cdot0 & 2\cdot0+6\cdot1 & 2\cdot5+6\cdot(-2) \\ 1\cdot1+4\cdot0 & 1\cdot2+4\cdot0 & 1\cdot0+4\cdot1 & 1\cdot5+4\cdot(-2) \end{bmatrix} = \begin{bmatrix} 1 & 2 & 3 & -1 \\ 2 & 4 & 6 & -2 \\ 1 & 2 & 4 & -3 \end{bmatrix}

我们发现结果不等于原始的 AA。哪里出错了？

关键修正：我们必须使用原始矩阵 AA 的主元列，而不是 RREF 后的主元列。 在这个例子中，我们正确地从 AA 中选取了第1和第3列作为 CC。

错误在于验证时的一个疏忽。让我们重新计算 CRCR 的第四列：

  • CC 的第1列 × RR 第1行第4列： 1×5=51 \times 5 = 5

  • CC 的第2列 × RR 第2行第4列： 3×(−2)=−63 \times (-2) = -6

  • 总和： 5+(−6)=−15 + (-6) = -1，但这与 AA 的第四列 [1,2,3]T[1, 2, 3]^T 不符。

这说明了一个重要问题：CR分解要求我们使用来自原始矩阵 AA 的线性无关列，但 RR 矩阵必须正确地表征这些列如何组合出整个 AA。 在这个例子中，我们的 RR 是从 RREF 直接取来的，但我们需要确保 CRC R 精确重构 AA。

实际上，正确的 RR 应该满足 A=CRA = C R。这意味着 RR 的列是 CC 的列表示 AA 的每一列的系数。我们可以通过求解 CR=AC R = A 来找到 RR，这正好是 RREF 过程所做的事情。因此，我们的步骤在理论上是正确的，但验证时需要仔细计算。

重新验证第四列：

  • CC 的第1列 × RR 第1行第4列： 1×5=51 \times 5 = 5

  • CC 的第2列 × RR 第2行第4列： 3×(−2)=−63 \times (-2) = -6

  • 第一行第四列结果： 5+(−6)=−15 + (-6) = -1

  • 第二行第四列： 2×5+6×(−2)=10−12=−22 \times 5 + 6 \times (-2) = 10 - 12 = -2

  • 第三行第四列： 1×5+4×(−2)=5−8=−31 \times 5 + 4 \times (-2) = 5 - 8 = -3

这得到了 [−1,−2,−3]T[-1, -2, -3]^T，但 AA 的第四列是 [1,2,3]T[1, 2, 3]^T。矛盾表明我可能在最初的 RREF 计算中出了错。

让我们重新计算 AA 的 RREF：

A=[123124621343]A = \begin{bmatrix} 1 & 2 & 3 & 1 \\ 2 & 4 & 6 & 2 \\ 1 & 3 & 4 & 3 \end{bmatrix}

步骤：

  1. R2 = R2 - 2*R1, R3 = R3 - R1:

[123100000112]\begin{bmatrix} 1 & 2 & 3 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 2 \end{bmatrix}

  1. Swap R2 and R3:

[123101120000]\begin{bmatrix} 1 & 2 & 3 & 1 \\ 0 & 1 & 1 & 2 \\ 0 & 0 & 0 & 0 \end{bmatrix}

  1. R1 = R1 - 2*R2:

[101−301120000]\begin{bmatrix} 1 & 0 & 1 & -3 \\ 0 & 1 & 1 & 2 \\ 0 & 0 & 0 & 0 \end{bmatrix}

所以正确的 RREF 是：

RREF(A)=[101−301120000]\text{RREF}(A) = \begin{bmatrix} \boxed{1} & 0 & 1 & -3 \\ 0 & \boxed{1} & 1 & 2 \\ 0 & 0 & 0 & 0 \end{bmatrix}

主元在第1列和第2列！所以秩 r=2r=2。

修正后的 Step 2: 构造矩阵 CC

  • CC 由 AA 的主元列（第1列和第2列）组成。

C=[122413]C = \begin{bmatrix} 1 & 2 \\ 2 & 4 \\ 1 & 3 \end{bmatrix}

修正后的 Step 3: 构造矩阵 RR

  • RR 就是 AA 的行最简形（RREF）中的非零行。

R=[101−30112]R = \begin{bmatrix} 1 & 0 & 1 & -3 \\ 0 & 1 & 1 & 2 \end{bmatrix}

修正后的 Step 4: 验证分解

CR=[122413][101−30112]=[1⋅1+2⋅01⋅0+2⋅11⋅1+2⋅11⋅(−3)+2⋅22⋅1+4⋅02⋅0+4⋅12⋅1+4⋅12⋅(−3)+4⋅21⋅1+3⋅01⋅0+3⋅11⋅1+3⋅11⋅(−3)+3⋅2]=[123124621343]=AC R = \begin{bmatrix} 1 & 2 \\ 2 & 4 \\ 1 & 3 \end{bmatrix} \begin{bmatrix} 1 & 0 & 1 & -3 \\ 0 & 1 & 1 & 2 \end{bmatrix} = \begin{bmatrix} 1\cdot1+2\cdot0 & 1\cdot0+2\cdot1 & 1\cdot1+2\cdot1 & 1\cdot(-3)+2\cdot2 \\ 2\cdot1+4\cdot0 & 2\cdot0+4\cdot1 & 2\cdot1+4\cdot1 & 2\cdot(-3)+4\cdot2 \\ 1\cdot1+3\cdot0 & 1\cdot0+3\cdot1 & 1\cdot1+3\cdot1 & 1\cdot(-3)+3\cdot2 \end{bmatrix} = \begin{bmatrix} 1 & 2 & 3 & 1 \\ 2 & 4 & 6 & 2 \\ 1 & 3 & 4 & 3 \end{bmatrix} = A

验证成功！

这个修正后的例子强调了正确计算 RREF 和识别主元列的重要性。

3. 为什么叫“CR”分解？

  • CC 代表 Column（列）或 Basis for the Column space（列空间的基）。

  • RR 代表 Row（行）或 Basis for the Row space（行空间的基），或者 Reduced（最简形）。

4. CR分解的性质与意义

  1. 列空间（Column Space）： Col(A)=Col(C)\text{Col}(A) = \text{Col}(C) 矩阵 CC 的列构成了 AA 的列空间的一组基。

  2. 行空间（Row Space）： Row(A)=Row(R)\text{Row}(A) = \text{Row}(R) 矩阵 RR 的行构成了 AA 的行空间的一组基。

  3. 秩（Rank）： rank(A)=rank(C)=rank(R)=r\text{rank}(A) = \text{rank}(C) = \text{rank}(R) = r 分解显式地给出了矩阵的秩。

  4. 唯一性（Uniqueness）：

  • 矩阵 RR （即RREF）是唯一的。

  • 矩阵 CC 的列来自 AA 的特定列（主元列），这部分选择是唯一的。但如果我们选择列空间的任意一组基来构成 CC，那么 RR 也会相应改变。所以，基于主元列的CR分解是唯一的。

  1. 与其它分解的关系：

  • 与QR分解的区别：QR分解要求 CC 的列是正交的（通过Gram-Schmidt过程得到），而CR分解中的 CC 只是原矩阵的列，不一定正交。

  • 与LU分解的区别：LU分解侧重于求解方程组的三角系统，而CR分解侧重于揭示矩阵的列和行空间结构。

5. 应用场景

  • 理解矩阵结构：CR分解是理解一个矩阵的列空间和行空间最直接的方式之一。

  • 低秩矩阵近似：在数据科学中，如果矩阵 AA 是近似低秩的，我们可以通过CR分解取前 rr 个主元列和前 rr 行来得到一个很好的低秩近似 A≈CrRrA \approx C_r R_r。

  • 理论推导：在线性代数的理论证明中，CR分解是一种非常有用的工具。

6. 总结

特性描述
形式A=CRA = C R
矩阵Cm×rm \times r 矩阵，由 AA 的 rr 个线性无关列（主元列）组成。
矩阵Rr×nr \times n 矩阵，是 AA 的行最简形（RREF） 的前 rr 行。
核心意义清晰地展示了矩阵的列空间和行空间的结构。
唯一性基于主元列的分解是唯一的。
主要应用理解矩阵结构、理论证明、低秩近似。

简单来说，CR分解告诉我们：原矩阵 AA 的所有列，都可以由 CC 中的“主元列”通过 RR 中的行系数线性组合而成。 它是一种非常直观和基础的分解。

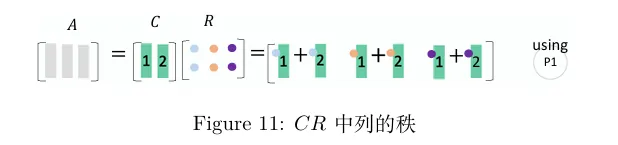
A=CRA=CR 分解图解

A=CR\boldsymbol{A}=\boldsymbol{C} \boldsymbol{R} 所有一般的长矩阵 AA 都有相同的行秩和列秩．这个分解是理解这一定理最直观的方法．CC 由 AA 的线性无关列组成，RR 为 AA 的行阶梯形矩阵（消除了零行）．A=CRA=C R 将 AA 化简为 rr 的线性无关列 CC 和线性无关行 RR的乘积．

A=CR[123235]=[1223][101011]\begin{aligned} A & =C R \\ {\left[\begin{array}{lll} 1 & 2 & 3 \\ 2 & 3 & 5 \end{array}\right] } & =\left[\begin{array}{ll} 1 & 2 \\ 2 & 3 \end{array}\right]\left[\begin{array}{lll} 1 & 0 & 1 \\ 0 & 1 & 1 \end{array}\right] \end{aligned}

推导过程：从左往右看 AA 的列。保留其中线性无关的列，去掉可以由前者线性表出的列。则第1、2列被保留，而第三列因为可以由前两列之和表示而被去掉。而要通过线性无关的 1、21 、 2 两列重新构造出 AA ，需要右乘一个行阶梯矩阵 RR ．

图片

现在你会发现行的秩为 2 ，因为 CC 中只有 2 个线性无关列．而 AA 中所有的列都可以由 CC 中的 2 列线性表出．

图片

前の章31._矩阵的LU分解
次の章33._矩阵的QR分解