行视角理解矩阵乘法
引入
想象我们是一家餐厅,使用三种原材料 水、面粉和调料 可以制作四种食物:面条、馒头、糕点和饼
 {width=500px}
{width=500px}
每种食物的配方是不同的,例如如下
10*水+3*面粉+2*调料=面条
5*水+3*面粉+0.5*调料=馒头
7*水+4*面粉+10*调料=糕点
4*水+1.5*面粉+4*调料=饼
单个产品
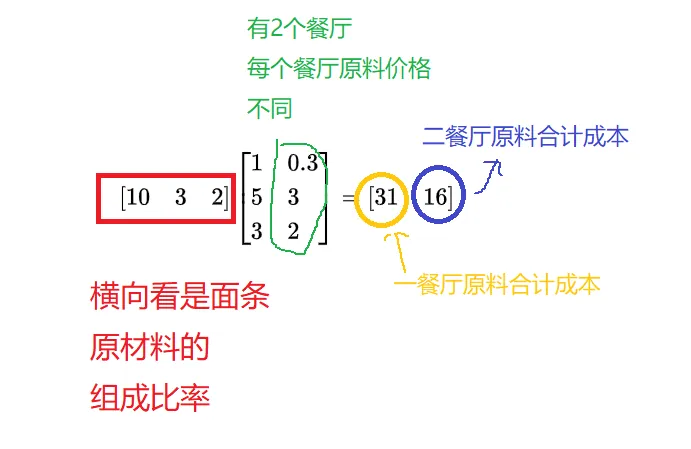
现在我们先考虑比较简单的情况:我们生成一种食物(面条),但是有两个餐馆,每个餐馆对原料的价格并不相同,即有
[1032]1530.332=[3116] 我们看一下矩阵乘积的现实意义:有一个产品,并且有2个餐厅(每种原料不同价格不同),矩阵乘法的结果是分别得到两个餐厅的原料价格。
多个产品
如果我们制作不止一个食品,因此把食品从一个变更为四个,毫无疑问矩阵乘积的结果也将变成四行,每行对应一个产品在每个餐厅的成本, 更具体的说,对不同的餐厅而言,三种原料的价格是不同的,第一个餐厅三种原料的价格分别是1,5,3,第二个餐厅三种原料的价格分别是0.3, 3, 2。于是有了下面的等式:
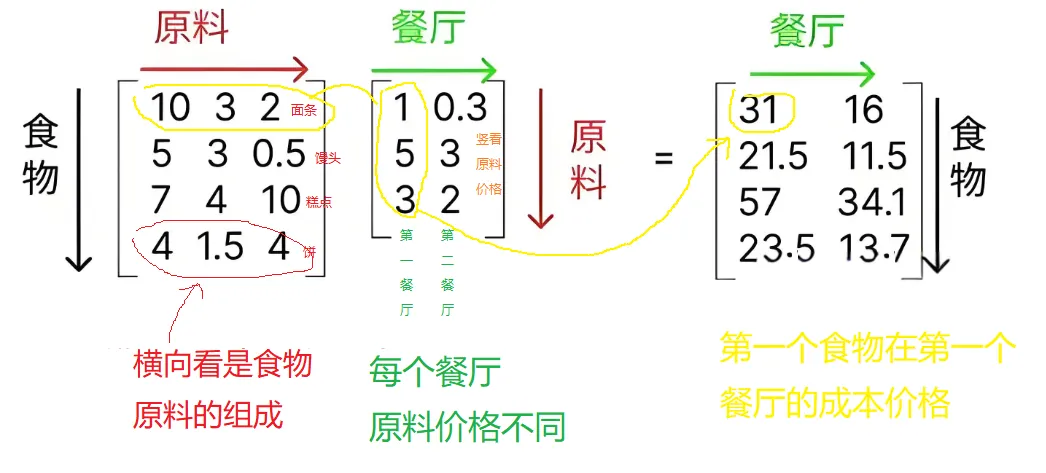
比如我们看 面条在第一个餐厅原料价格就是: 10∗1+3∗5+2∗3=31 ,面条在第二个餐厅原料价格就是: 10∗0.3+3∗3+2∗2=16 ,馒头在第一个餐厅的成本是21.5,在第二个餐厅成本价格是11.5,以此类推,最终形成了结果矩阵。
我们能够感觉到:上面的计算矩阵的结果是总价,因此是降维的。换句话说,原料消失了变成了食物,比如一个三维空间球体投影到平面上变成了椭圆,这就是维度降低
行视角图解
矩阵左乘行向量,向量对矩阵的行进行线性组合,结果向量位于矩阵的行空间
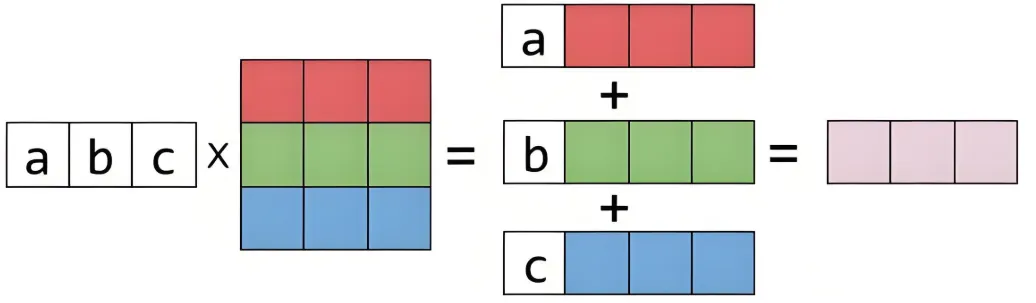
左侧的向量可以延展为一个由若干行所组成的矩阵,每一行乘以右边的矩阵,得到结果矩阵中的一行。
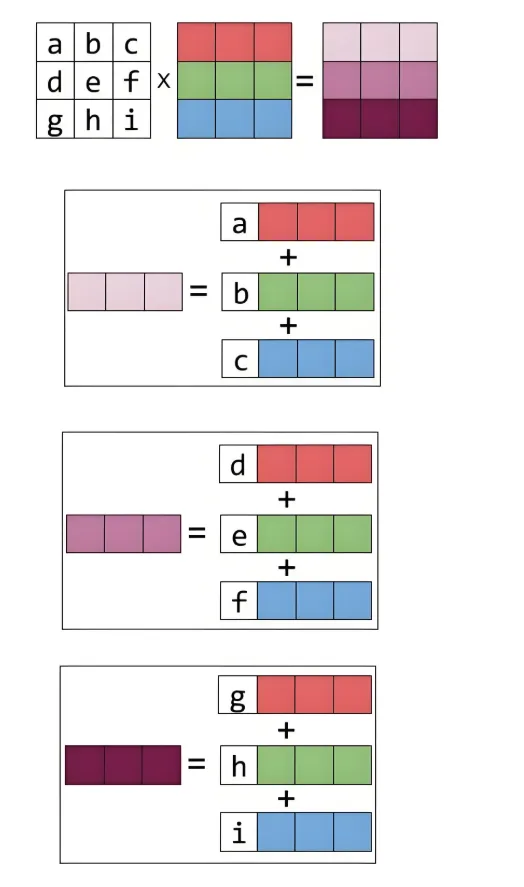
行视角下的方程组
设有方程
⎩⎨⎧a11x1+a12x2+⋯+a1nxn=b1a21x1+a22x2+⋯+a2nxn=b2⋯⋯⋯an1x1+an2x2+⋯+annxn=bn 则方程可以写成
[x1x2...xn]a11a12...an1a12...a22...an2...a1na2nann=[b1b2...bn] 这种记法用的并不是很多,我们一直说过,矩阵行视角其实并不方便人类大脑的思考。在上面这种记法可以进行转置处理,转换为列向量
因为XA=B, 如果两边取转置就有 ATXT=BT ,这样就把行向量转换为列向量,又回到了我们熟悉的列模式了。 在 逆矩阵求解方程组 里, 我们就是这么干的。
行视角下的矩阵乘法
考虑下面2个矩阵相乘
[123]111222=[612] 可以发现,原本3维的行向量经过矩阵乘法后变成了2维的列向量,因此采用行视角,可以简单理解为对向量进行升维或者将维
 {width=500px}
{width=500px}


