矩阵的LU分解的概念
设 A 是 n×n 矩阵,他可以被分解为一个下三角矩阵L和上三角矩阵U相乘的形式。其中L矩阵主对角线都是1.
提示:LU分解里,L是Low(下)的意思,U是Upper(上)的意思 不是每个矩阵都可以LU分解
A=1■■■01■■001■0001■000■■00■■■0■■■□ 分解条件:并非所有矩阵都能进行LU分解,需要满足以下条件:
① 矩阵是方阵
② 被分解方阵是可逆的,即该矩阵是满秩矩阵;
③ 消元过程中没有0主元出现,即不能出现主对角线都是0的情况;
为什么需要LU分解?
LU分解的主要目的是高效求解线性方程组 Ax=b。
分解:首先将 A 分解为 L 和 U。
Ax=b⟹(LU)x=b⟹L(Ux)=b 引入中间变量:令 Ux=y,原方程变为:Ly=b
下三角:因为 L 是下三角矩阵,方程组 Ly=b 非常容易求解(从上往下代换)。
上三角:得到 y 后,再求解 Ux=y。因为 U 是上三角矩阵,这个方程组也非常容易求解(从下往上代换)。
因此, LU 分解核心就2句话:①先通过 LY=b 求解出 Y ②再通过 UX=Y 求解出 X
优势:
对于需要多次求解不同 b 但 A 不变的情况(非常常见),只需做一次昂贵的 LU 分解,之后每次求解的成本很低。
比直接使用高斯消元法更高效、更数值稳定。
LU分解的实现
假设 A 可以化为阶梯形 U ,化简过程中仅用行倍加变换,即把一行的倍数加于它下面的另一行.这样,存在单位下三角初等矩阵 E1,⋯,Ep 使
Ep⋯E1A=U...(1) 于是
A=(Ep⋯E1)−1U=LU 其中
L=(Ep⋯E1)−1...(2) 可以看到(1)(2)分别就得到了U,L
注意(1)中的行变换,它把 A 化为 U ,所以也把(2)中的 L 化为 I ,这是因为
Ep⋯E1L=(Ep⋯E1)(Ep⋯E1)−1=I 这一点是构造 L 的关键.
注意:在上面求解L过程中,可以使用逆矩阵计算,即公式(2)也可以使用在变化过程中使用的变量进行计算,下面的例子会演示使用变量直接生成下三角。
分解方法:高斯消元法
LU分解本质上就是记录高斯消元过程。
矩阵 U 就是高斯消元结束后得到的上三角矩阵。
矩阵 L 是由消元过程中所用的乘数(即为了消元而乘以的系数)构成的,并且这些乘数放在了下三角位置。
计算步骤(以 3x3 矩阵为例):
设矩阵 A=248137129
Step 1: 第一列消元
目标:将 a21 和 a31 变为 0。
乘数:
l21=24=2 (用第1行消去第2行的第一个元素)
l31=28=4 (用第1行消去第3行的第一个元素)
消元后的矩阵 A(1):
2001(3−2×1)(7−4×1)1(2−2×1)(9−4×1)=200113105 Step 2: 第二列消元
目标:将 a32(1) 变为 0。
乘数:
l32=13=3 (用第2行消去第3行的第二个元素)
消元后的矩阵 U:
20011010(5−3×0)=200110105 构造 L 和 U:
U 就是最终的上三角矩阵: U=200110105
L 由乘数和对角线1构成: L=1l21l3101l32001=124013001
注意:上面的L的矩阵元素2,4,3直接使用所乘的系数进行拼接。
验证:
LU=124013001200110105=248137129=A
1. 存在性与选主元(Pivoting)
存在性:并非所有矩阵都有LU分解。当且仅当 A 的所有顺序主子式均不为零时,LU分解才存在。
例如,矩阵 [0110] 就不能直接进行LU分解。
选主元(Pivoting):为了解决上述问题并提高数值稳定性,通常使用部分选主元(Partial Pivoting)。这会在分解过程中引入一个置换矩阵 P,使得分解变为:
这意味着我们先对矩阵 A 的行进行交换,然后再对交换后的矩阵进行 LU 分解。这在所有数值计算软件(如MATLAB, NumPy)中都是标准做法。
2. LDU分解
LU分解的一个变种是LDU分解,它将一个对角矩阵 D 分离出来:
其中 L 是下三角矩阵(对角线为1),U 是上三角矩阵(对角线为1),D 是对角矩阵。这有时可以使分解更加对称。
3. 总结
| 特性 | 描述 |
|---|
| 形式 | A=LU(或 PA=LU) |
| 矩阵L | 下三角矩阵,主对角线元素为1,其余元素是高斯消元的乘数。 |
| 矩阵U | 上三角矩阵,是高斯消元的最终结果。 |
| 应用 | 高效求解线性方程组、计算矩阵的逆、计算行列式(det(A)=det(L)det(U)=∏uii)。 |
| 优点 | 一次分解,多次使用。是数值计算中最基础的分解之一。 |
| 注意 | 需要选主元来保证数值稳定性和解决存在性问题。 |
简单来说,LU分解就是高斯消元法的“矩阵形式”,它将消元的过程信息完美地记录在了 L 和 U 两个矩阵中。
A=LU分解图解
下图摘自 《The Art of Linear Algebra》 给出的图解,采用递归的方法,适合计算机处理。
用高斯消除法求解 Ax=b 也被称为 LU 分解。通常,是 A 左乘一个初等行变换矩阵 (E) 来得到一个上三角矩阵 U 。
EAA let L=E−1,A=U=E−1U=LU 现在,求解 Ax=b 有2步:(1)求解 Lc=b ,(2)代回 Ux=c .
在这里,我们直接通过 A 计算 L 和 U .
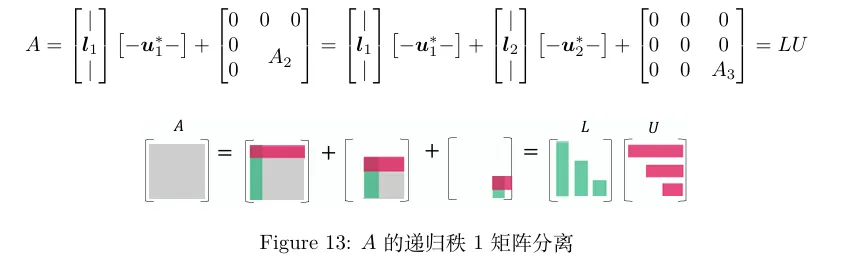
要计算 L 和 U ,首先分离出由 A 的第一行和第一列组成的外积.余下的部分为 A2 .递归执行此操作,将 A 分解为秩1矩阵之和.
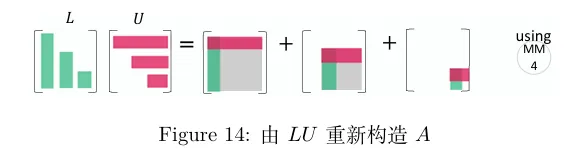
由 L 乘以 U 来重新构造 A 则相对简单。

