3._三阶行列式的几何意义 - 线性代数

三阶行列式的定义

参考上一节二阶行列式的顶用，下面给出三阶行列式的定义：

\begin{aligned} &|\boldsymbol{A}|=\left|\begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right|, \end{aligned}

称 $|\boldsymbol{A}|$ 是一个三阶行列式. 我们要定义三阶行列式的值, 使得行列式具有上节中所述的 8 个性质. 我们不妨倒过来, 假定行列式已经定义且适合 8 个性质, 那么行列式 $|\boldsymbol{A}|$ 的值应该等于什么?

根据二行列式性质6 , 上述行列式 $|\boldsymbol{A}|$ 可以表示成为 3 个行列式之和:

|\boldsymbol{A}|=\left|\begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ 0 & a_{22} & a_{23} \\ 0 & a_{32} & a_{33} \end{array}\right|+\left|\begin{array}{ccc} 0 & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ 0 & a_{32} & a_{33} \end{array}\right|+\left|\begin{array}{ccc} 0 & a_{12} & a_{13} \\ 0 & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right| .

对于上述和式中的第二个行列式, 利用性质 4 , 将其第二行和第一行对换, 就可将它化为与和式中第一个行列式相同的类型. 同理, 和式中第三个行列式也可以通过行对换化为和第一个行列式相同的类型. 因此, 现在的问题是, 行列式

\left|\begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ 0 & a_{22} & a_{23} \\ 0 & a_{32} & a_{33} \end{array}\right|

应该等于什么? 我们利用性质 7 可以将上面这个行列式化为上三角行列式:将 $-a_{22}^{-1} a_{32}$ 乘以第二行加到第三行上, 由性质 7 , 行列式值不变, 即

\left|\begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ 0 & a_{22} & a_{23} \\ 0 & a_{32} & a_{33} \end{array}\right|=\left|\begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ 0 & a_{22} & a_{23} \\ 0 & 0 & a_{33}-a_{22}^{-1} a_{32} a_{23} \end{array}\right|

再根据性质1，有

\begin{aligned} \left|\begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ 0 & a_{22} & a_{23} \\ 0 & 0 & a_{33}-a_{22}^{-1} a_{32} a_{23} \end{array}\right| & =a_{11} a_{22}\left(a_{33}-a_{22}^{-1} a_{32} a_{23}\right) \\ & =a_{11}\left(a_{22} a_{33}-a_{32} a_{23}\right) \\ & =a_{11}\left|\begin{array}{cc} a_{22} & a_{23} \\ a_{32} & a_{33} \end{array}\right| \end{aligned}

于是

\left|\begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ 0 & a_{22} & a_{23} \\ 0 & a_{32} & a_{33} \end{array}\right|=a_{11}\left|\begin{array}{ll} a_{22} & a_{23} \\ a_{32} & a_{33} \end{array}\right|

再由性质 4 和上面的结果, 我们得到

\begin{aligned} \left|\begin{array}{ccc} 0 & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ 0 & a_{32} & a_{33} \end{array}\right|=-a_{21}\left|\begin{array}{ll} a_{12} & a_{13} \\ a_{32} & a_{33} \end{array}\right|, \end{aligned}

和

\begin{aligned} \left|\begin{array}{ccc} 0 & a_{12} & a_{13} \\ 0 & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right|=a_{31}\left|\begin{array}{ll} a_{12} & a_{13} \\ a_{22} & a_{23} \end{array}\right| \end{aligned}

可以看到，利用上一节介绍的二阶行列式的性质，就可以倒推出三阶行列式的值。

代数余子式 现在我们引进几个名词. 如果将上述行列式 $|\boldsymbol{A}|$ 划去某个元素 $a_{i j}(i, j=$ $1,2,3)$ 所在的一行和一列, 则剩下的元素按原来的次序组成一个二阶行列式, 我们称这个二阶行列式为元素 $a_{i j}$ 的余子式, 记为 $M_{i j}$ .

比如 $|\boldsymbol{A}|$ 中元素 $a_{11}$ 的余子式为 $M_{11}=\left|\begin{array}{cc}a_{22} & a_{23} \\ a_{32} & a_{33}\end{array}\right|$ , 元素 $a_{12}$ 的余子式为 $M_{12}=\left|\begin{array}{ll}a_{21} & a_{23} \\ a_{31} & a_{33}\end{array}\right|$ , 元素 $a_{23}$ 的余子式为 $M_{23}=\left|\begin{array}{ll}a_{11} & a_{12} \\ a_{31} & a_{32}\end{array}\right|$ , 等等.

根据上面的分析, 我们有理由作出如下的定义. $|\boldsymbol{A}|$ 的值为

|\boldsymbol{A}| =|\boldsymbol{A}|=a_{11} M_{11}-a_{21} M_{21}+a_{31} M_{31} .

为了便于记忆，三阶行列式的值可以写成

\begin{aligned} &\left|\begin{array}{lll} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{array}\right| \\ &=a_1 \cdot\left|\begin{array}{ll} b_2 & b_3 \\ c_2 & c_3 \end{array}\right|-a_2 \cdot\left|\begin{array}{ll} b_1 & b_3 \\ c_1 & c_3 \end{array}\right|+a_3 \cdot\left|\begin{array}{ll} b_1 & b_2 \\ c_1 & c_2 \end{array}\right| \\ &=a_1 b_2 c_3+a_2 b_3 c_1+a_3 b_1 c_2-a_1 b_3 c_2-a_2 b_1 c_3-a_3 b_2 c_1 \end{aligned}

三阶行列式的值可以这么算：他是3主对角线元素的和减去3个副对角线元素的和。

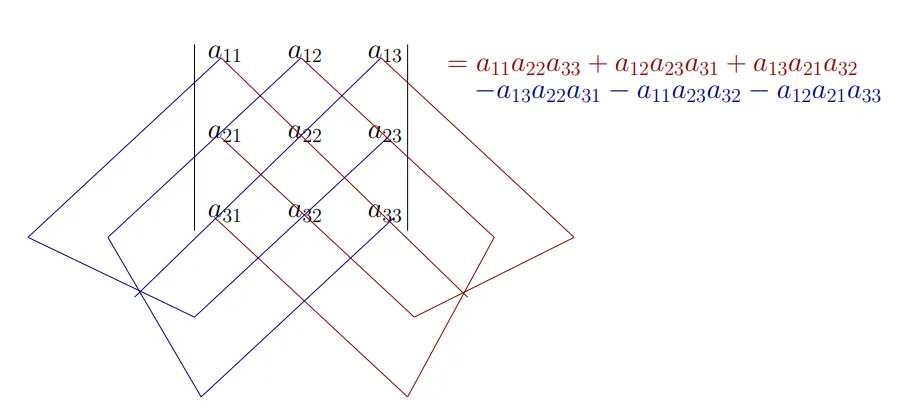$图片$ {width=600px}

三阶行列式的计算

对于三阶行列式计算通常使用三种方法：（1）代数余子式（2）初等变换。（3）利用对角线法则

①利用代数余子式计算三阶行列式

通过代数余子式，把三阶行列式转换为多个二阶的行列式，也就是行列式按行展开。点击查看代数余子式教程

例计算 ${D}_3=\left|\begin{array}{lll} {a}_{11} & {a}_{12} & {a}_{13} \\ {a}_{21} & {a}_{22} & {a}_{23} \\ {a}_{31} & {a}_{32} & {a}_{33}\end{array}\right|$

解：以第一行展开, 得

\begin{aligned} {D}_3 & =(-1)^{1+1} {a}_{11} {M}_{11}+(-1)^{1+2} {a}_{12} {M}_{12}+(-1)^{1+3} {a}_{13} {M}_{13} \\ & = {a}_{11}\left|\begin{array}{ll} {a}_{22} & {a}_{23} \\ {a}_{32} & {a}_{33} \end{array}\right|- {a}_{12}\left|\begin{array}{ll} {a}_{21} & {a}_{23} \\ {a}_{31} & {a}_{33} \end{array}\right|+ {a}_{13}\left|\begin{array}{ll} {a}_{21} & {a}_{22} \\ {a}_{31} & {a}_{32} \end{array}\right| \end{aligned}

二阶的大家都会算，这里就不再进一步展开了。

例 计算三阶行列式 $D=\left|\begin{array}{rrr}3 & -1 & 2 \\ 1 & 2 & -1 \\ 2 & 1 & 4\end{array}\right|$ . 解：按第一行展开, 得

\begin{aligned} D & =3 \times(-1)^{1+1}\left|\begin{array}{rr} 2 & -1 \\ 1 & 4 \end{array}\right|+(-1) \times(-1)^{1+2}\left|\begin{array}{rr} 1 & -1 \\ 2 & 4 \end{array}\right|+2 \times(-1)^{1+3}\left|\begin{array}{ll} 1 & 2 \\ 2 & 1 \end{array}\right| \\ & =3 \times 9+6+2 \times(-3)=27 \end{aligned}

例计算

\begin{aligned} D=\left|\begin{array}{lll} 1 & 0 & 0 \\ 2 & 3 & 5 \\ 4 & 6 & 7 \end{array} \right| \end{aligned}

按照第一行展开

\begin{aligned} & D=\left|\begin{array}{lll} 1 & 0 & 0 \\ 2 & 3 & 5 \\ 4 & 6 & 7 \end{array}\right|=1 \times(-1)^{1+1}\left|\begin{array}{ll} 3 & 5 \\ 6 & 7 \end{array}\right|+0 \times(-1)^{1+2}\left|\begin{array}{cc} 2 & 5 \\ 4 & 7 \end{array}\right|+0 \times(-1)^{1+3}\left|\begin{array}{ll} 2 & 3 \\ 4 & 6 \end{array}\right| \\ & =21-30 \\ & =-9 \end{aligned}

②利用行列式性质计算三阶行列式

利用行列式性质计算三阶行列式，主要是把行列式转换为上三角或者下三角，然后其值为主对角线的乘积。

在转换时，核心是利用行列式的3个性质： ①若行列式中有两行 (或两列) 对应元素相等，则行列式等于零. ②若行列式的某一行 (或列) 有公因子 $k$ ，则公因子 $k$ 可以提到行列式记号外面 ③行列式某一行 (或某一列) 的 $k$ 倍加到另一行 (或另一列) 的对应元素上去，行列式的值不变.

例计算 $\left|\begin{array}{ccc}1 & 2 & 3 \\ 2 & 4 & 6 \\ -3 & 7 & -2\end{array}\right|$ 解：观察到第二行恰好是第一行的2倍, 于是直接有

\begin{aligned} &\left|\begin{array}{ccc} 1 & 2 & 3 \\ 2 & 4 & 6 \\ -3 & 7 & -2 \end{array}\right|=0 \end{aligned}

例 计算

\left|\begin{array}{lll} 2 & 3 & -5 \\ 0 & 2 & -1 \\ 0 & 0 & -2 \end{array}\right|

解：该行列式是上三角行列式，因此直接有

\left|\begin{array}{lll} 2 & 3 & -5 \\ 0 & 2 & -1 \\ 0 & 0 & -2 \end{array}\right|=2 \times 2 \times(-2)=-8

例 计算

0 & 1 & 2 \\ 2 & 1 & 1 \\ -1 & 3 & 1 \end{array}\right|

解：仔细观察此行列式，第一列已经有一个0，如果第二行第一个元素也是0，那么就可以直接用代数余子式展开，为此利用行列式的性质：行列式某一行 (或某一列) 的 $k$ 倍加到另一行 (或另一列) 的对应元素上去，行列式的值不变.来化简

将第3行的2倍加到第二行上去，然后展开可得

\left|\begin{array}{ccc} 0 & 1 & 2 \\ 2 & 1 & 1 \\ -1 & 3 & 1 \end{array}\right| \xrightarrow{2 \mathrm{r}_3 \rightarrow \mathrm{r}_2}\left|\begin{array}{ccc} 0 & 1 & 2 \\ 0 & 7 & 3 \\ -1 & 3 & 1 \end{array}\right|=(-1) \times\left|\begin{array}{ll} 1 & 2 \\ 7 & 3 \end{array}\right|=11 .

③利用对角线法则计算

对于形如如下的三阶行列式，其值为主对角线（红色）减去副对角线（蓝色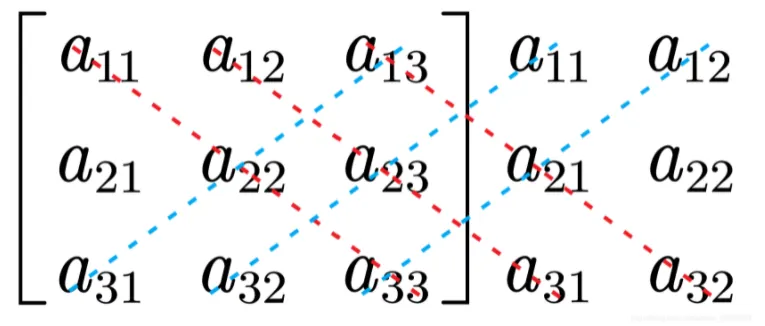） $图片$ {width=200px} 即：

{D}_3= {a}_{11} {a}_{22} {a}_{33}+ {a}_{12} {a}_{23} {a}_{31}+ {a}_{13} {a}_{21} {a}_{32} - {a}_{13} {a}_{22} {a}_{31}- {a}_{11} {a}_{23} {a}_{32}- {a}_{12} {a}_{21} {a}_{33}

例计算三阶行列式 $D=\left|\begin{array}{rrr}3 & -1 & 2 \\ 1 & 2 & -1 \\ 2 & 1 & 4\end{array}\right|$ . 解：利用对角线法则, 得

\begin{aligned} D= & 3 \times 2 \times 4+(-1) \times(-1) \times 2+2 \times 1 \times 1 \\ & -3 \times(-1) \times 1-(-1) \times 1 \times 4-2 \times 2 \times 2 \\ = & 24+2+2+3+4-8=27 . \end{aligned}

化为上三角计算三阶行列式

在三阶行列式技术中，最常用的还是化为上三角计算三阶行列式。行列式最终的要一个性质：

行列式某一行 (或某一列) 的 $k$ 倍加到另一行 (或另一列) 的对应元素上去，行列式的值不变.

例 计算 $A=\left[\begin{array}{rrr}1 & -4 & 2 \\ -2 & 8 & -9 \\ -1 & 7 & 0\end{array}\right]$ ．

解思路是先将 $A$ 化为上三角，以第一行为基准,使用第一行的2倍加到第二行上去的

A=\left|\begin{array}{rrr} 1 & -4 & 2 \\ -2 & 8 & -9 \\ -1 & 7 & 0 \end{array}\right|=\left|\begin{array}{rrr} 1 & -4 & 2 \\ 0 & 0 & -5 \\ -1 & 7 & 0 \end{array}\right|

使用第一行的1倍加到第三行上去的

A=\left|\begin{array}{rrr} 1 & -4 & 2 \\ 0 & 0 & -5 \\ 0 & 3 & 2 \end{array}\right|

交换第 2 行与第 3 行使行列式取反号，即

A=-\left|\begin{array}{rrr} 1 & -4 & 2 \\ 0 & 3 & 2 \\ 0 & 0 & -5 \end{array}\right|=-(1)(3)(-5)=15

在下一节会详细介绍如何化为上三角或下三角。

三阶行列式的几何意义

一个 $3 \times 3$ 阶的行列式是其行向量或列向量所张成的平行六面体的有向体积。这个结论可以从两个向量所张成的平行四边形推知。如图 3-12 所示, 由两个向量 $\boldsymbol{a} 、 \boldsymbol{b}$ 张成的平行四边形为 $o \boldsymbol{a} P \boldsymbol{b}$ , 面积 $S$ 为 $\boldsymbol{a} 、 \boldsymbol{b}$ 构成的行列式。那么沿着第三个向量 $\boldsymbol{c}$ 方向生长出无数个平行于原四边形的新的平行四边形来, 直至到向量 $\boldsymbol{c}$ 的末端为止。显然, 所有的这些平行四边形构成一个以向量 $a 、 b 、 c$ 为棱的平行六面体，这些四边形的面积叠加起来正是平行六面体的体积。 $图片$

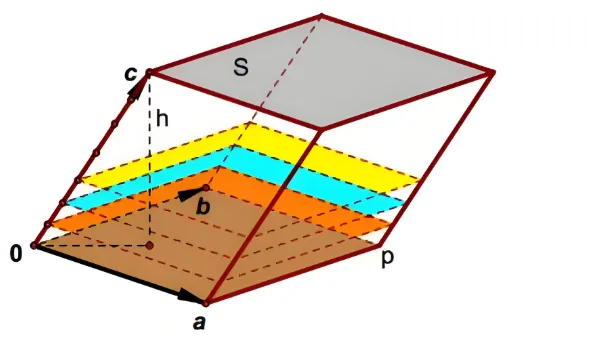
由此可以推知 $n$ 阶行列式表示的是 $n$ 个向量所张成的体积。

参考上图，现在知道了三阶行列式可以看成三个向量 $a,b,c$ 张成的立方体的体积，那接下来就有一个问题：在哪些情况下 $a,b,c$ 无法张成立方体？

情况1：两个向量共线，无法张成空间体积

即 $a,b,c$ 中，只要有2个向量在一条直线上就无法张成空间体积。特别的 $a,b,c$ 三个向量再一条直线上可以看成2个向量共线的基础上，又一个也共线，自然更无法张成空间体积。

情况2：三个向量共面，无法张成空间体积

$a,b,c$ 在一个平面上自然无法张成空间体积。

在 情况1 和 情况2 下，不用计算就知道其行列式的值为零。

示例1:下面1个3阶行列式，因为各个分量成比例，也就是3个向量共线，体积为零，所以其值为零。

A=-\left|\begin{array}{rrr} 1 & 2 & 3 \\ 2 & 4 & 6 \\ 3 & 6 & 9 \end{array}\right|=0

示例2:

A=-\left|\begin{array}{rrr} 1 & 3 & 5 \\ 2 & 4 & 6 \\ 0 & 0 & 0 \end{array}\right|=0

3个向量(1,2,0),(3,4,0),(5,6,0) 第三个分量都在 $xy$ 平面上，也就是这3个向量共面，所以体积为零。自然行列式的值为零。

总结

对于2阶行列式，如果2个向量共线则组成的“体积”为零。对于3阶行列式，如果2个向量共线或3个向量共面，则“体积”为零。对于4阶行列式，如果4个行列式向量共线或者共面或者共体，则“体积”为零。以此类推。

通过对2阶、3阶和4阶的套路，就可以推广到 $n$ 阶，此结果只能慢慢自己体会。

特别的，如果这 $n$ 个向量里，如果有一个成比例，就无法张成向量空间，空间发生了坍塌，其值就是零。请记住这个结论。