13._范德蒙德行列式与拉格朗日插值 - 线性代数

范德蒙行列式

形如

$D_n=\left|\begin{array}{cccc}1 & 1 & \cdots & 1 \\ x_1 & x_2 & \cdots & x_n \\ \vdots & \vdots & \ddots & \vdots \\ x_1^{n-1} & x_2^{n-1} & \cdots & x_n^{n-1}\end{array}\right|$ 。

的行列式被称呼为 $n$ 阶的范德蒙德 (Vandermonde) 行列式。他的值为 $n$ 阶范德蒙行列式 $D_n= \prod_{1 \leq j<i \leq n}\left(x_i-x_j\right)$

①这里 $\prod$ 是连乘的符号。 ②请注意上面的连乘 $1 \leq j<i \leq n$ ,注意后面是 $j<i$ ，不能是 $j \leq i$ ，否则就变成0了。

记忆方法 盯着第二行，后一项减前一项的所有项的乘积。 $图片$

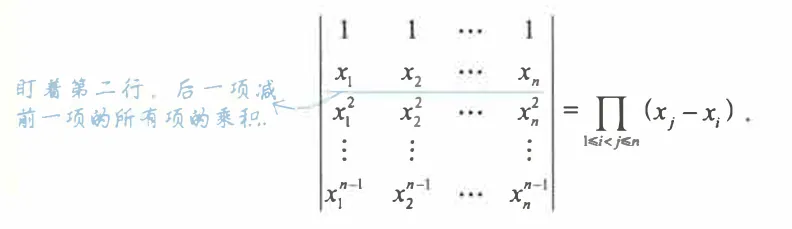
当n=3的范德蒙行列式

当 $n=3$ 的情况， $D_3=\left|\begin{array}{ccc}1 & 1 & 1 \\ x_1 & x_2 & x_3 \\ x_1^2 & x_2^2 & x_3^2\end{array}\right|=\left(x_2-x_1\right)\left(x_3-x_2\right)\left(x_3-x_1\right)$

当n=4的范德蒙行列式

当 $n=4$ 的情况

D_4=\left|\begin{array}{cccc} 1 & 1 & 1 & 1 \\ x_1 & x_2 & x_3 & x_4 \\ x_1^2 & x_2^2 & x_3^2 & x_4^2 \\ x_1^3 & x_2^3 & x_3^3 & x_4^3 \end{array}\right|=\left(x_2-x_1\right)\left(x_3-x_1\right)\left(x_4-x_1\right)\left(x_3-x_2\right)\left(x_4-x_2\right)\left(x_4-x_3\right)

例题

例计算

2 & 2 & 2 & 2 \\ 1 & 2 & 3 & 4 \\ 1 & 4 & 9 & 16 \\ 1 & 8 & 27 & 64 \end{array}\right| .

解：第一行可以提取出公因子2，则余下的就是范德蒙行列式。

只看第二行数据，即盯着第二行，后一项减前一项的所有项的乘积。

D=2\left|\begin{array}{cccc} 1 & 1 & 1 & 1 \\ 1 & 2 & 3 & 4 \\ 1 & 4 & 9 & 16 \\ 1 & 8 & 27 & 64 \end{array}\right|=2(2-1)(3-1)(4-1)(3-2)(4-2)(4-3)=24 .

注意：因为转置行列式与行列式的值相等，在考试时，有时候老师会反过来写，比如

D_2=\left|\begin{array}{cccc} 1 & 1 & 1 & 1 \\ 1 & 2 & 4 & 8 \\ 1 & 3 & 9 & 27 \\ 1 & 4 & 16 & 64 \end{array}\right|

此时，你也需要认出这是范德蒙行列式，不要写成转置，你就不认识他了。

例 计算

D=\left|\begin{array}{cccccc} a_1^n & a_1^{n-1} b_1 & a_1^{n-2} b_1^2 & \cdots & a_1 b_1^{n-1} & b_1^n \\ a_2^n & a_2^{n-1} b_2 & a_2^{n-2} b_2^2 & \cdots & a_2 b_2^{n-1} & b_2^n \\ \vdots & \vdots & \vdots & & \vdots & \vdots \\ a_{n+1}^n & a_{n+1}^{n-1} b_{n+1} & a_{n+1}^{n-2} b_{n+1}^2 & \cdots & a_{n+1} b_{n+1}^{n-1} & b_{n+1}^n \end{array}\right| .

分析首先认清这是一个 $(n+1)$ 阶的行列式．其次构成本行列式元素的特点是：第 $i$ 行的元素，由 $a_i$ 的降幂及 $b_i$ 的升幂排列． $a_i$ 由 $n$ 次降为零次， $b_i$ 由零次升为 $n$ 次。根据这一特点，若每一行分别提出公因子 $a_i^n$ 后，就变成 $\left(\frac{b_i}{a_i}\right)$ 的升幂排列：从零次到 $n$ 次——这就是一个 $(n+1)$ 阶的 Vandermonde行列式

解

\begin{aligned} D_{n+1} & =a_1^n \cdot a_2^n \cdots a_{n+1}^n \cdot\left|\begin{array}{cccc} 1 & \left(\frac{b_1}{a_1}\right) & \left(\frac{b_1}{a_1}\right)^2 & \cdots \\ 1 & \left(\frac{b_2}{a_2}\right) & \left(\frac{b_1}{a_1}\right)^n \\ \vdots & \cdots & \vdots & \left(\frac{b_2}{a_2}\right)^n \\ 1 & \left(\frac{b_{n+1}}{a_{n+1}}\right) & \left(\frac{b_{n+1}}{a_{n+1}}\right)^2 & \cdots \\ & \left(\frac{b_{n+1}}{a_{n+1}}\right)^n \end{array}\right| \\ & =a_1^n \cdot a_2^n \cdots a_{n+1}^n V_{n+1}\left(\frac{b_1}{a_1}, \frac{b_2}{a_2}, \cdots, \frac{b_{n+1}}{a_{n+1}}\right) \\ & =a_1^n \cdot a_2^n \cdots a_{n+1}^n \cdot \prod_{1 \leqslant j<i \leqslant n+1}\left(\frac{b_i}{a_i}-\frac{b_j}{a_j}\right) . \end{aligned}

范德蒙行列式的意义

范德蒙行列式主要用在拉格朗日插值上。在多项式理论里，有一个理论：给定 $n+1$ 个点，能够求出一个 $n$ 次多项式出来，例如给定4个点，能够求出一个3次多项式，给定5个点，能求出一个4次多项式。

假设给定5个点， $(-3,-1),(-2,1),(0,-0.5),(1,0),(3,1.5)$ 带入一个四次方程里, $y=a_0+a_1 x^1+a_2 x^2 +a_3 x^3 +a_4 x^4$ 这个方程整理后，就是

\left\{\begin{aligned} -1 & =a_0+a_1(-3)+a_2(-3)^2+a_3(-3)^3+a_4(-3)^4 \\ 1 & =a_0+a_1(-2)+a_2(-2)^2+a_3(-2)^3+a_4(-2)^4 \\ -0.5 & =a_0+a_1(0)+a_2(0)^2+a_3(0)^3+a_4(0)^4 \\ 0 & =a_0+a_1(1)+a_2(1)^2+a_3(1)^3+a_4(1)^4 \\ 1.5 & =a_0+a_1(3)+a_2(3)^2+a_3(3)^3+a_4(3)^4 \end{aligned}\right.

五个未知数，五个方程，所以方程有唯一解。将上面的方程组，写成矩阵乘法的形式，系数矩阵就是范德蒙矩阵

\begin{aligned} &\left[\begin{array}{c} -1 \\ 1 \\ -0.5 \\ 0 \\ 1.5 \end{array}\right]=\left[\begin{array}{ccccc} 1 & -3 & (-3)^2 & (-3)^3 & (-3)^4 \\ 1 & -2 & (-2)^2 & (-2)^3 & (-2)^4 \\ 1 & 0 & 0^2 & 0^3 & 0^4 \\ 1 & 1 & 1^2 & 1^3 & 1^4 \\ 1 & 3 & 3^2 & 3^3 & 3^4 \end{array}\right]\left[\begin{array}{l} a_0 \\ a_1 \\ a_2 \\ a_3 \\ a_4 \end{array}\right] \end{aligned}

拉格朗日插值基本思想

我们构造出一个形如下式的多项式

P(x)=\sum_{i=1}^n y_i l_i(x)

什么意思呢？，我们以对 $\left(x_1, y_1\right),\left(x_2, y_2\right),\left(x_3, y_3\right)$ 三个点插值为例。

此时的 $P(x)$ 为

P(x)= y_1 l_1(x)+y_2 l_2(x)+y_3 l_3(x)

出于一种简单的思考，我们想要 $l(x)$ 满足下面的关系：

当我们代入 $x_1$ 得到函数 $P(x)$ 时， $l_1\left(x_1\right)=1, l_2\left(x_1\right)=0, l_3\left(x_1\right)=0$ ，这使得 $P\left(x_1\right)=y_1$ ．相同的，当我们代入 $x_2$ 到函数 $P(x)$ 时， $l_1\left(x_2\right)=0, l_2\left(x_2\right)=1, l_3\left(x_2\right)=0$ ，这使得 $P\left(x_2\right)$ $=y_2$

当我们代入 $x_3$ 到函数 $P(x)$ 时， $l_1\left(x_3\right)=0, l_2\left(x_3\right)=0, l_3\left(x_3\right)=1$ ，这使得 $P\left(x_3\right)=y_3$ ．

什么样的 $l(x)$ 满足这样的性质？

如果对 $l_1(x)$ 来讲，其需要满足当 $x_1$ 被代入时 $l_1\left(x_1\right)=1$ ，代入 $x_2, x_3$ 时输出0这两个性质．不难想到如果 $l_1(x)=\left(x-x_2\right)\left(x-x_3\right)$ 满足代入 $x_2, x_3$ 输出 0 的性质。

此时，如果代入 $x_1, ~ l_1\left(x_1\right)=\left(x_1-x_2\right)\left(x_1-x_3\right)$ ，容易注意到如果修改 $l_1(x)$ 为 $l_1(x)=\dfrac{\left(x-x_2\right)\left(x-x_3\right)}{\left(x_1-x_2\right)\left(x_1-x_3\right)}$ ，则 $l_1\left(x_1\right)=1$ 性质也就被满足了．这样我们就构造出了子函数。

进一步理解

下面简单介绍一下拉格朗日插值。我们先从一个简单的二次函数入手，假设平面上，有一个抛物线，经过 $(1,0)$ 和 $(3,0)$ 两个点，我们怎么求这个抛物线？我们可以设置抛物线的方程为 $y=a(x-1)(x-3)$ 把这2个坐标点带进去就可以求出 $a$ ，进而求出抛物线方程。

用通常的思想，现在平面上有三个点， $\left(x_1, y_1\right),\left(x_2, y_2\right),\left(x_3, y_3\right)\left(x_1<x_2<x_3\right)$ ，我们现在用它们算插值.

根据中学基础知识，我们知道，这三个点肯定可以唯一确定一个二次函数。

那么我们就尝试找到它，怎么找？拉格朗日想到了一个比较粗暴的方法：对于每个点都搞一个子函数 $f_i(x)$ ，要求 $f_i(x)$ 在 $x=x_i$ 的时候得到 1 ，在 $x=x_j(j \neq i)$ 的时候得到 0 ，把 $n$ 个子函数凑起来，得到的函数不就过了 $n$ 个点了! 也就是说，我们要计算 $n$ 个子函数，第 $i$ 个子函数为:

f_i(x)= \begin{cases}1 & x=x_i \\ 0 & x=x_j(j \neq i) \\ I \text { don't care } & \text { otherwise }\end{cases}

那么插值的结果就是:

f(x)=\sum_{i=1}^n y_i f_i(x)

回到原问题上面来. 考虑构造 $f_1(x)$ ，对于 $f_1\left(x_j\right)=0(j>1)$ 的情况很好满足，可以想到:

f_1(x)=(x-x 2)(x-x 3)

怎么让 $f_1\left(x_1\right)=1$ 呢? 我们只需要把不用的丢掉就好:

f_1(x)=\dfrac{\left(x-x_2\right)\left(x-x_3\right)}{\left(x_1-x_2\right)\left(x_1-x_3\right)}

仔细观察 $f_1(x)$ ,也就是这个抛物线应该过 $(x_1,1),(x_2,0),(x_3, 0)$ ，我们把 $(x_2,0),(x_3,_0)$ 称作基点。

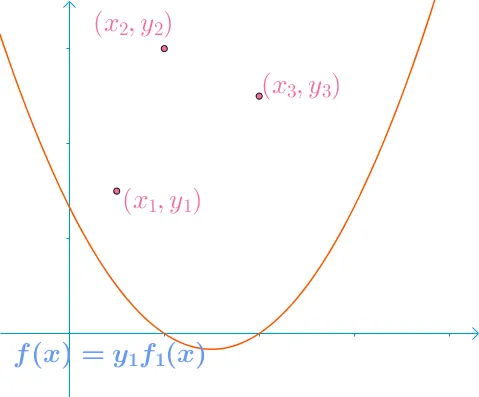
所以最后就有 $f_1(x)$ 长成下面这个样子

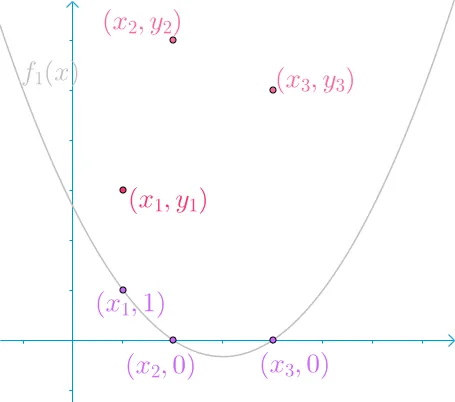$图片$ {width=300px}

同理构造出 $f_2(x)$ ,如下，他通过 $(x_2,1)$ ，并通过 $(x_1,0),(x_3,0)$ 这2个基点。 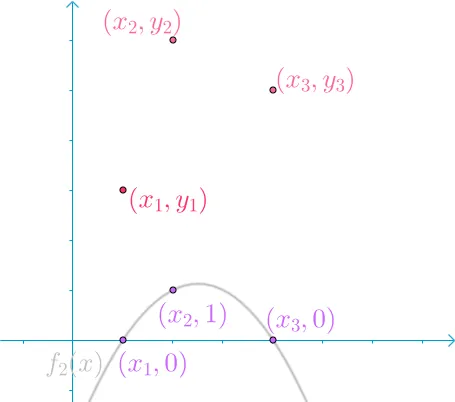$图片$ {width=300px}

和 $f_3(x)$ :，他通过 $(x_3,1)$ ，并通过 $(x_1,0),(x_2,0)$ 这2个基点。 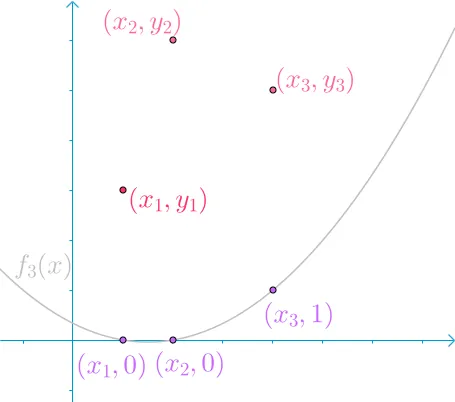$图片$ {width=300px}

求和得到 $f(x)$ : $f(x)=\frac{y_1(x-x_2)(x-x_3)}{(x_1-x_2)(x_1-x_3)}+\frac{y_2(x-x_1)(x-x_3)}{(x_2-x_1)(x_2-x_3)}+\frac{y_3(x-x_1)(x-x_2)}{(x_3-x_1)(x_3-x_2)}$

$v2-369e7b90a0dd39b52123216e3790e1fd_hd.gif$

这样就得到了通过这3点的拟合抛物线。

推广到一般形式: 对于 $n$ 个点 $\left(x_1, y_1\right),\left(x_2, y_2\right), \ldots,\left(x_n, y_n\right)\left(x_1<x_2<\ldots<x_n\right)$ ，设:

f_i(x)=\frac{\prod_{j \neq i}\left(x-x_j\right)}{\prod_{j \neq i}\left(x_i-x_j\right)}

那么插值结果就是:

f(x)=\sum_{i=1}^n y_i f_i(x)=\sum_{i=1}^n y_i \times \frac{\prod_{j \neq i}\left(x-x_j\right)}{\prod_{j \neq i}\left(x_i-x_j\right)}

$\prod \limits_{j \ne i} (x - x_j)$ 决定了 $L(x)$ 的次数, 一共有 $n-1$ 个形如 $(x - k)$ (视 $x_j$ 为常数 $k$ ) 的东西相乘, 那么它就是 $n-1$ 次多项式( $n$ 次数界多项式). 这个公式可以这样记录: $L(x) = \sum_{i=0}^{n-1} y_i \ell_i(x)$ $\ell_i(x) = \prod_{j=0,j\ne i}^{n-1} \frac{(x - x_j)}{(x_i - x_j)} = \frac{(x - x_0) \cdots (x - x_{i-1})(x - x_{i+1}) \cdots (x - x_{n-1})}{(x_i - x_0) \cdots (x_i - x_{i-1})(x_i - x_{i+1}) \cdots (x_i - x_{n-1})}$ 其中 $\ell_i(x)$ 称为拉格朗日基本多项式

例1：假设有某个二次多项式函数 $f$ ，已知它在三个点上的取值为: $f(4)=10, f(5)=5.25, f(6)=1$ ，求 $f(18)$ 的值。解：首先写出每个拉格朗日基本多项式:

\begin{aligned} & l_0(x)=\frac{(x-5)(x-6)}{(4-5)(4-6)} \\ & l_1(x)=\frac{(x-4)(x-6)}{(5-4)(5-6)} \\ & l_2(x)=\frac{(x-4)(x-5)}{(6-4)(6-5)} \end{aligned}

然后应用拉格朗日插值法，就可以得到 $P$ 的表达式（ $P$ 为函数 $f$ 的插值函数）:

P(x)=f(4) l_0(x)+f(5) l_1(x)+f(6) l_2(x)

代入我们上面的公式:

P(x)=\frac{1}{4}\left(x^2-28 x+136\right)

此时代入数值18就可以得到所求之值:

f(18)=P(18)=-11