向量组等价的几何解释 两个向量组 A A A B B B A A A B \boldsymbol{B} B B \boldsymbol{B} B A A A
两个向量组等价就是两个向量组所扩张成的直线、平面或空间相互重合
下面讨论的是三维空间中向量组的等价关系。
单位为了更好理解向量组的等价,我们先给出一个概念:向量组的秩,他的详细介绍会在 此处
假设给你n n n n n n n n n 例如含有3个向量的 ( [ 1 1 ] , [ 2 2 ] , [ 3 3 ] ) \left( \left[\begin{array}{l} 1 \\ 1 \end{array}\right] , \left[\begin{array}{l} 2 \\ 2 \end{array}\right] , \left[\begin{array}{l} 3 \\ 3 \end{array}\right] \right) ( [ 1 1 ] , [ 2 2 ] , [ 3 3 ] )
假设给你n n n n n n n n n 。例如含有3个向量的 ( [ 1 1 ] , [ 2 2 ] , [ 3 4 ] ) \left( \left[\begin{array}{l} 1 \\ 1 \end{array}\right] , \left[\begin{array}{l} 2 \\ 2 \end{array}\right] , \left[\begin{array}{l} 3 \\ 4 \end{array}\right] \right) ( [ 1 1 ] , [ 2 2 ] , [ 3 4 ] )
假设给你n n n n n n n n n 例如含有3个向量的 ( [ 1 0 0 ] , [ 0 1 0 ] , [ 0 0 1 ] ) \left( \left[\begin{array}{l} 1 \\ 0 \\0 \end{array}\right] , \left[\begin{array}{l} 0 \\ 1 \\ 0\end{array}\right] , \left[\begin{array}{l} 0 \\ 0 \\1 \end{array}\right] \right) 1 0 0 , 0 1 0 , 0 0 1
以此类推。理解了上面的结论后,下面再进一步细细解释上面的结果。
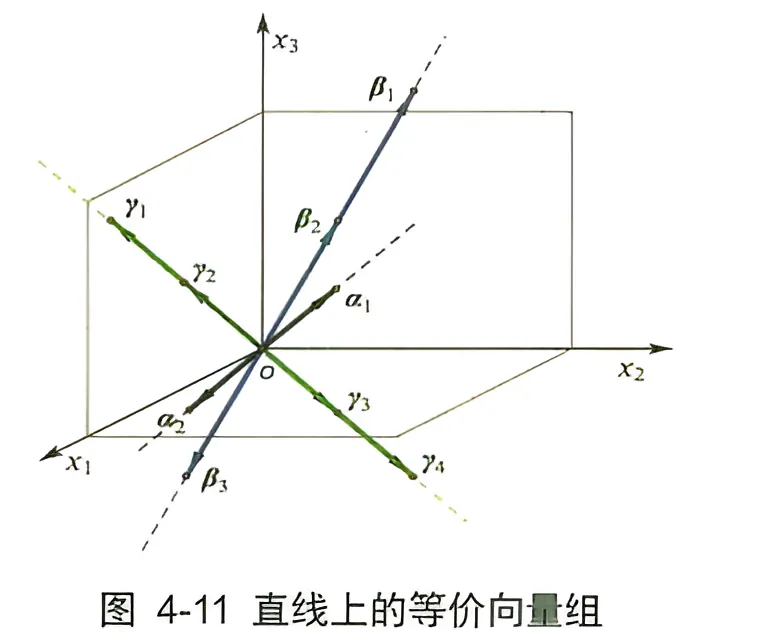
直线上的等价向量组 如图 4-11 所示的三维空间中, 共有三条分离的不共面直线, 每条直线上分别有两个、三个和四个向量。两向量 α 1 、 α 2 \alpha_1 、 \alpha_2 α 1 、 α 2 β 1 、 β 2 、 β 3 \beta_1 、 \beta_2 、 \beta_3 β 1 、 β 2 、 β 3 γ 1 、 γ 2 、 γ 3 、 γ 4 \gamma_1 、 \gamma_2 、 \gamma_3 、 \gamma_4 γ 1 、 γ 2 、 γ 3 、 γ 4
由此, 我们可以验证以下命题:
{ α 1 } , { α 2 } , { α 1 , α 2 } \left\{\alpha_1\right\},\left\{\alpha_2\right\},\left\{\alpha_1, \alpha_2\right\} { α 1 } , { α 2 } , { α 1 , α 2 }
{ β 1 } , { β 2 } , { β 3 } , { β 1 , β 2 } , { β 1 , β 3 } , { β 2 , β 3 } , { β 1 , β 2 , β 3 } \left\{\boldsymbol{\beta}_1\right\},\left\{\boldsymbol{\beta}_2\right\},\left\{\boldsymbol{\beta}_3\right\},\left\{\boldsymbol{\beta}_1, \boldsymbol{\beta}_2\right\},\left\{\boldsymbol{\beta}_1, \boldsymbol{\beta}_3\right\},\left\{\boldsymbol{\beta}_2, \boldsymbol{\beta}_3\right\},\left\{\boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \boldsymbol{\beta}_3\right\} { β 1 } , { β 2 } , { β 3 } , { β 1 , β 2 } , { β 1 , β 3 } , { β 2 , β 3 } , { β 1 , β 2 , β 3 }
{ γ 1 } . . . { γ 4 } , { γ 1 , γ 2 } , { γ 1 , γ 3 } . . . { γ 3 , γ 4 } \left\{\gamma_1\right\} ...\left\{\gamma_4\right\},\left\{\gamma_1, \gamma_2\right\},\left\{\gamma_1, \gamma_3\right\} ...\left\{\gamma_3, \gamma_4\right\} { γ 1 } ... { γ 4 } , { γ 1 , γ 2 } , { γ 1 , γ 3 } ... { γ 3 , γ 4 } { γ 1 , γ 2 , γ 3 } , { γ 1 , γ 2 , γ 4 } , . . . { γ 1 , γ 2 , γ 3 , γ 4 } \left\{\gamma_1, \gamma_2, \gamma_3\right\},\left\{\gamma_1, \gamma_2, \gamma_4\right\},...\left\{\gamma_1, \gamma_2, \gamma_3, \gamma_4\right\} { γ 1 , γ 2 , γ 3 } , { γ 1 , γ 2 , γ 4 } , ... { γ 1 , γ 2 , γ 3 , γ 4 }
其实上述命题不用验证也可以知道, 因为我们罗列的等价向量组里的向量都包含在一条直线上, 每个向量组都扩张成同一根直线。
从这里不难得出第一个结论:
假设给你n n n n n n n n n
如果我们使用更具体的数字来验证,比如有3个向量
a 1 = ( 1 1 1 ) , a 2 = ( 3 3 3 ) ; a 2 = ( 4 4 4 ) ; \boldsymbol{a_1}=\left(\begin{array}{r}
1 \\
1 \\
1
\end{array}\right), \quad \boldsymbol{a_2}=\left(\begin{array}{l}
3 \\
3 \\
3
\end{array}\right) ;
\quad \boldsymbol{a_2}=\left(\begin{array}{l}
4 \\
4 \\
4
\end{array}\right) ; a 1 = 1 1 1 , a 2 = 3 3 3 ; a 2 = 4 4 4 ; 因为这些坐标成比例,所以这3个向量的秩为1,所以这3个向量在一条直线上。如果写出这三个向量的矩阵为
( 1 3 4 1 3 4 1 3 4 ) \left(\begin{array}{ccc}
1 & 3 & 4 \\
1 & 3 & 4 \\
1 & 3 & 4 \\
\end{array}\right) 1 1 1 3 3 3 4 4 4 可以发现他们的秩正好也为1
平面等价向量组: 类似地, 三维空间中, 我们看看平面上的向量组之间的等价关系。如图 4-12 所示, 向量 α i 、 β i 、 η i \boldsymbol{\alpha}_i 、 \boldsymbol{\beta}_i 、 \boldsymbol{\eta}_i α i 、 β i 、 η i α i 、 β i 、 η i \boldsymbol{\alpha}_i 、 \boldsymbol{\beta}_i 、 \boldsymbol{\eta}_i α i 、 β i 、 η i α i = x 1 β i + x 2 η i \boldsymbol{\alpha}_i=x_1 \boldsymbol{\beta}_i+x_2 \boldsymbol{\eta}_i α i = x 1 β i + x 2 η i
α i 、 β i 、 η i \boldsymbol{\alpha}_i 、 \boldsymbol{\beta}_i 、 \boldsymbol{\eta}_i α i 、 β i 、 η i C 3 2 \mathrm{C}_3^2 C 3 2 C 3 3 \mathrm{C}_3^3 C 3 3
{ α i , β i } , { α i , η i } , { β i , η i } , { α i , β i , η i } \left\{\boldsymbol{\alpha}_i, \boldsymbol{\beta}_i\right\},\left\{\boldsymbol{\alpha}_i, \boldsymbol{\eta}_i\right\},\left\{\boldsymbol{\beta}_i, \boldsymbol{\eta}_i\right\},\left\{\boldsymbol{\alpha}_i, \boldsymbol{\beta}_i, \boldsymbol{\eta}_i\right\} { α i , β i } , { α i , η i } , { β i , η i } , { α i , β i , η i } { α 1 , β 2 } , { α 2 , η 1 } , { β 1 , β 2 , η 2 } \left\{\boldsymbol{\alpha}_1, \boldsymbol{\beta}_2\right\},\left\{\boldsymbol{\alpha}_2, \boldsymbol{\eta}_1\right\},\left\{\boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \boldsymbol{\eta}_2\right\} { α 1 , β 2 } , { α 2 , η 1 } , { β 1 , β 2 , η 2 }
从这里不难得出第二个结论:
假设给你n n n n n n n n n
把上面结论用具体向量来解释,比如有下面2个向量
a 1 = ( 1 1 0 ) , a 2 = ( 1 2 0 ) ; \boldsymbol{a_1}=\left(\begin{array}{r}
1 \\
1 \\
0
\end{array}\right), \quad \boldsymbol{a_2}=\left(\begin{array}{l}
1 \\
2 \\
0
\end{array}\right) ; a 1 = 1 1 0 , a 2 = 1 2 0 ; 因为他们的第三个分量都是0,所以,他们在X O Y XOY XO Y
如果写出这两个向量的矩阵为
( 1 1 1 2 0 0 ) \left(\begin{array}{ccc}
1 & 1 \\
1 & 2\\
0 & 0
\end{array}\right) 1 1 0 1 2 0 可以发现矩阵的秩为2
三维空间上的向量组 参考图4-12,如果一个平面再加一个平面外的一条直线 γ \gamma γ
{ α i , β i , γ i } , { α i , η i , γ i } , { β i , η i , γ i } , { α i , β i , η i , γ i } \left\{\boldsymbol{\alpha}_i, \boldsymbol{\beta}_i, \gamma_i\right\},\left\{\boldsymbol{\alpha}_i, \boldsymbol{\eta}_i, \gamma_i\right\},\left\{\boldsymbol{\beta}_i, \boldsymbol{\eta}_i, \boldsymbol{\gamma}_i\right\},\left\{\boldsymbol{\alpha}_i, \boldsymbol{\beta}_i, \boldsymbol{\eta}_i, \gamma_i\right\} { α i , β i , γ i } , { α i , η i , γ i } , { β i , η i , γ i } , { α i , β i , η i , γ i } { α 1 , β 2 , γ 1 } , { α 2 , η 1 , γ 2 } \left\{\boldsymbol{\alpha}_1, \boldsymbol{\beta}_2, \gamma_1\right\},\left\{\boldsymbol{\alpha}_2, \boldsymbol{\eta}_1, \gamma_2\right\} { α 1 , β 2 , γ 1 } , { α 2 , η 1 , γ 2 } { β 1 , β 2 , η 2 , γ 1 , γ 3 } , { α 1 , α 2 , β 1 , β 2 , η 1 , η 2 , γ 1 , γ 2 , γ 3 , γ 4 } \left\{\boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \boldsymbol{\eta}_2, \gamma_1, \gamma_3\right\},\left\{\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \boldsymbol{\eta}_1, \boldsymbol{\eta}_2, \boldsymbol{\gamma}_1, \boldsymbol{\gamma}_2, \gamma_3, \gamma_4\right\} { β 1 , β 2 , η 2 , γ 1 , γ 3 } , { α 1 , α 2 , β 1 , β 2 , η 1 , η 2 , γ 1 , γ 2 , γ 3 , γ 4 }
因此,可以得到
假设给你n n n n n n n n n
通过上面的例子,大致理解了向量组等价的意义。
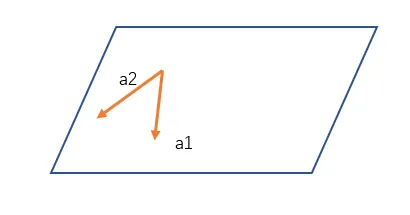
秩相等不代表可以互相表示 情况1:假设有2个向量共面,如下图, 小提示:此时秩 r ( a 1 , a 2 ) = 2 r(a_1,a_2)=2 r ( a 1 , a 2 ) = 2
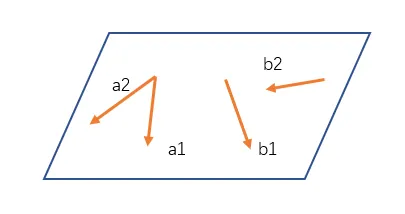
情况2:假设有4个向量共面,如下图,小提示:此时秩 r ( a 1 , a 2 , b 1 , b 2 ) = 2 r(a_1,a_2,b_1,b_2)=2 r ( a 1 , a 2 , b 1 , b 2 ) = 2
如果记向量组 A = ( a 1 , a 2 ) A=(a_1,a_2) A = ( a 1 , a 2 ) B = ( b 1 , b 2 ) B=(b_1,b_2) B = ( b 1 , b 2 ) r ( A ) = 2 r(A)=2 r ( A ) = 2 r ( B ) = 2 r(B)=2 r ( B ) = 2 r ( A ∣ B ) = 2 r(A|B)=2 r ( A ∣ B ) = 2
如果向量组 A A A B B B A A A B B B A A A B B B
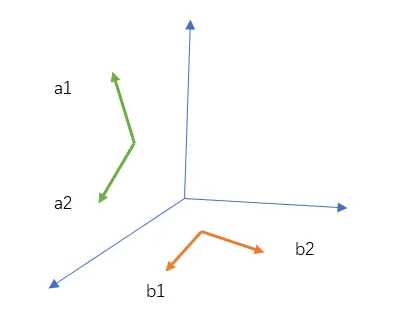
但是,他们的逆命题不一定成立,请看下面示意图
A = ( a 1 , a 2 ) A=(a_1,a_2) A = ( a 1 , a 2 ) B = ( b 1 , b 2 ) B=(b_1,b_2) B = ( b 1 , b 2 ) 不能 相互表示,此时,可以看到r ( A ) = 2 r(A)=2 r ( A ) = 2 r ( B ) = 2 r(B)=2 r ( B ) = 2 r ( A B ) = 3 r(AB)=3 r ( A B ) = 3
所以,两个向量组的秩相等,不代表他们可以互相表示。
如何判断2组向量是否等价 通过上面的解释,我们可以得到两个向量组能否线性表示的解决方法:给你两个向量组,把这2个向量组组成一个矩阵,然后判断 R ( A ) = R ( B ) = R ( A B ) R(A)=R(B)=R(AB) R ( A ) = R ( B ) = R ( A B )
例 设
a 1 = ( 1 − 1 1 − 1 ) , a 2 = ( 3 1 1 3 ) , b 1 = ( 2 0 1 1 ) , b 2 = ( 1 1 0 2 ) , b 3 = ( 3 − 1 2 0 ) , a _1=\left(\begin{array}{r}
1 \\
-1 \\
1 \\
-1
\end{array}\right), a _2=\left(\begin{array}{l}
3 \\
1 \\
1 \\
3
\end{array}\right), b _1=\left(\begin{array}{l}
2 \\
0 \\
1 \\
1
\end{array}\right), b _2=\left(\begin{array}{l}
1 \\
1 \\
0 \\
2
\end{array}\right), b _3=\left(\begin{array}{r}
3 \\
-1 \\
2 \\
0
\end{array}\right), a 1 = 1 − 1 1 − 1 , a 2 = 3 1 1 3 , b 1 = 2 0 1 1 , b 2 = 1 1 0 2 , b 3 = 3 − 1 2 0 , 证明向量组 a 1 , a 2 a _1, a _2 a 1 , a 2 b 1 , b 2 , b 3 b _1, b _2, b _3 b 1 , b 2 , b 3
证明:向量组 a 1 , a 2 a _1, a _2 a 1 , a 2 b 1 , b 2 , b 3 b _1, b _2, b _3 b 1 , b 2 , b 3 R ( A ) = R ( B ) = R ( A B ) R(A)=R(B)=R(AB) R ( A ) = R ( B ) = R ( A B )
( A , B ) = ( 1 3 2 1 3 − 1 1 0 1 − 1 1 1 1 0 2 − 1 3 1 2 0 ) ( A , B )=\left(\begin{array}{rrrrr}
1 & 3 & 2 & 1 & 3 \\
-1 & 1 & 0 & 1 & -1 \\
1 & 1 & 1 & 0 & 2 \\
-1 & 3 & 1 & 2 & 0
\end{array}\right) ( A , B ) = 1 − 1 1 − 1 3 1 1 3 2 0 1 1 1 1 0 2 3 − 1 2 0 → ( 1 3 2 1 3 0 4 2 2 2 0 − 2 − 1 − 1 − 1 0 6 3 3 3 ) \to \left(\begin{array}{rrrrr}
1 & 3 & 2 & 1 & 3 \\
0 & 4 & 2 & 2 & 2 \\
0 & -2 & -1 & -1 & -1 \\
0 & 6 & 3 & 3 & 3
\end{array}\right) → 1 0 0 0 3 4 − 2 6 2 2 − 1 3 1 2 − 1 3 3 2 − 1 3 → ( 1 3 2 1 3 0 2 1 1 1 0 0 0 0 0 0 0 0 0 0 ) \to \left(\begin{array}{lllll}
1 & 3 & 2 & 1 & 3 \\
0 & 2 & 1 & 1 & 1 \\
0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0
\end{array}\right)
→ 1 0 0 0 3 2 0 0 2 1 0 0 1 1 0 0 3 1 0 0 可见, R ( A ) = 2 , R ( A , B ) = 2 . \text { 可见, } R( A )=2, R( A , B )=2 \text {. } 可见 , R ( A ) = 2 , R ( A , B ) = 2 . 对于向量组B的秩虽然可以直接求,但是还可以利用一个性质: B B B ( A B ) (AB) ( A B )
容易看出矩阵 B B B R ( B ) ⩾ 2 R( B ) \geqslant 2 R ( B ) ⩾ 2
R ( B ) ⩽ R ( A , B ) = 2 , R( B ) \leqslant R( A , B )=2, R ( B ) ⩽ R ( A , B ) = 2 , 于是知 R ( B ) = 2 R( B )=2 R ( B ) = 2
R ( A ) = R ( B ) = R ( A , B ) R( A )=R( B )=R( A , B ) R ( A ) = R ( B ) = R ( A , B ) 故向量组 a 1 , a 2 a_1, a_2 a 1 , a 2 b 1 , b 2 , b 3 b _1, b _2, b _3 b 1 , b 2 , b 3
例设向量
a 1 = ( 1 − 1 2 4 ) , a 2 = ( 0 3 1 2 ) ; b 1 = ( 3 0 7 14 ) , b 2 = ( 2 1 5 10 ) , \boldsymbol{a_1}=\left(\begin{array}{r}
1 \\
-1 \\
2 \\
4
\end{array}\right), \quad \boldsymbol{a_2}=\left(\begin{array}{l}
0 \\
3 \\
1 \\
2
\end{array}\right) ; \quad \boldsymbol{b_1}=\left(\begin{array}{r}
3 \\
0 \\
7 \\
14
\end{array}\right), \quad \boldsymbol{b_2}=\left(\begin{array}{r}
2 \\
1 \\
5 \\
10
\end{array}\right), a 1 = 1 − 1 2 4 , a 2 = 0 3 1 2 ; b 1 = 3 0 7 14 , b 2 = 2 1 5 10 , 向量组 A : a 1 , a 2 A: \boldsymbol{a_1, a_2} A : a 1 , a 2 B : b 1 , b 2 B: \boldsymbol{b _1, b _2} B : b 1 , b 2
(1)证明向量组 A A A B B B A A A B B B A A A B B B
( a 1 , a 2 , b 1 , b 2 ) = ( 1 0 3 2 − 1 3 0 1 2 1 7 5 4 2 14 10 ) \left(a_1, a_2, b_1, b_2\right)=\left(\begin{array}{rrrr}
1 & 0 & 3 & 2 \\
-1 & 3 & 0 & 1 \\
2 & 1 & 7 & 5 \\
4 & 2 & 14 & 10
\end{array}\right) ( a 1 , a 2 , b 1 , b 2 ) = 1 − 1 2 4 0 3 1 2 3 0 7 14 2 1 5 10 ∼ ( 1 0 3 2 0 3 3 3 0 1 1 1 0 2 2 2 ) \sim \left(\begin{array}{llll}
1 & 0 & 3 & 2 \\
0 & 3 & 3 & 3 \\
0 & 1 & 1 & 1 \\
0 & 2 & 2 & 2
\end{array}\right) ∼ 1 0 0 0 0 3 1 2 3 3 1 2 2 3 1 2 ∼ ( 1 0 3 2 0 1 1 1 0 0 0 0 0 0 0 0 ) . \sim \left(\begin{array}{llll}
1 & 0 & 3 & 2 \\
0 & 1 & 1 & 1 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0
\end{array}\right) . ∼ 1 0 0 0 0 1 0 0 3 1 0 0 2 1 0 0 . 于是,向量 b 1 b_1 b 1 b 2 b_2 b 2
{ b 1 = 3 a 1 + a 2 b 2 = 2 a 1 + a 2 \left\{\begin{array}{l}
b_1=3 a_1+a_2 \\
b_2=2 a_1+a_2
\end{array}\right. { b 1 = 3 a 1 + a 2 b 2 = 2 a 1 + a 2 也即向量组 B B B A A A
( b 1 , b 2 ) = ( a 1 , a 2 ) ( 3 2 1 1 ) = ( a 1 , a 2 ) K \left(b_1, b_2\right)=\left(a_1, a_2\right)\left(\begin{array}{ll}
3 & 2 \\
1 & 1
\end{array}\right)=\left(a_1, a_2\right) K ( b 1 , b 2 ) = ( a 1 , a 2 ) ( 3 1 2 1 ) = ( a 1 , a 2 ) K 其中,矩阵 K = ( 3 2 1 1 ) K =\left(\begin{array}{ll}3 & 2 \\ 1 & 1\end{array}\right) K = ( 3 1 2 1 ) K K K K − 1 = ( 1 − 2 − 1 3 ) K ^{-1}=\left(\begin{array}{rr}1 & -2 \\ -1 & 3\end{array}\right) K − 1 = ( 1 − 1 − 2 3 )
( a 1 , a 2 ) = ( b 1 , b 2 ) ( 1 − 2 − 1 3 ) , \left(a_1, a_2\right)=\left(b_1, b_2\right)\left(\begin{array}{rr}
1 & -2 \\
-1 & 3
\end{array}\right), ( a 1 , a 2 ) = ( b 1 , b 2 ) ( 1 − 1 − 2 3 ) , 具体写出,有
{ a 1 = b 1 − b 2 a 2 = − 2 b 1 + 3 b 2 \left\{\begin{array}{l}
a_1=b_1-b_2 \\
a_2=-2 b_1+3 b_2
\end{array}\right. { a 1 = b 1 − b 2 a 2 = − 2 b 1 + 3 b 2 从上知两向量组能相互线性表示,故它们等价.
上面例2的解法跳步比较大,可能有部分同学看不懂,请参考 向量组的等价 进行的解释
 {width=500px}
{width=500px}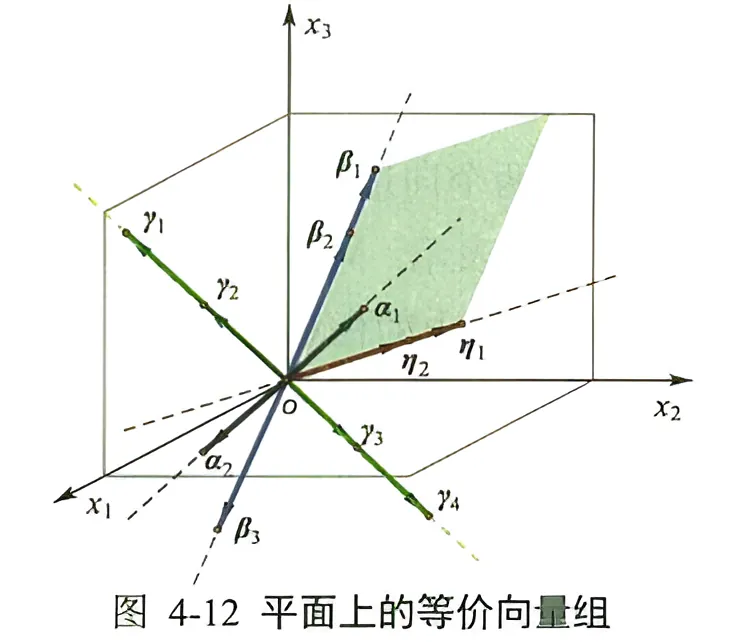 {width=500px}
换句话说, 向量 的任意 和 组合的向量组所张成的向量空间都是同一个平面。因此, 所有组合都是等价向量组。具体的等价关系如下:
{width=500px}
换句话说, 向量 的任意 和 组合的向量组所张成的向量空间都是同一个平面。因此, 所有组合都是等价向量组。具体的等价关系如下:
 {width=500px}
{width=500px}