13.4_CUDA实现
13.4 CUDA实现
设计扫描算法和学习电路图是很有启发的,但为了实现CUDA的扫描算法,我们需要将算法映射到寄存器、内存和寻址方案以及正确的同步。扫描的最佳CUDA实现依赖于将要执行的扫描的规模。针对线程束大小的扫描、可以放入共享内存的扫描以及必然会溢出到全局内存的扫描,要使用不同的方案。因为线程块之间不能可靠地通过全局内存交换数据,扫描因太大而无法放入共享内存的数据时,必须执行多个内核启动。[1]
在考察特殊情况(如断定的扫描)之前,我们将研究3种在CUDA中实现扫描的方法:
·先扫描再扇出(递归);
·先归约再扫描(递归);
两阶段先归约再扫描。
13.4.1 先扫描再扇出
先扫描再扇出的方法对于全局内存和共享内存,均使用类似的分解方案。图13-12显示了用于扫描一个线程块的方法:每32线程构成的
线程束执行一次扫描,并且该32个元素构成的子数组的归约值写入到共享内存。随后,单个线程束扫描数组的部分和。只需使用单个线程束就已足够,是因为CUDA不支持超过1024个线程的线程块。最后,基本和被扇出给每个线程束的输出元素。注意,图13-12中显示的步骤2所执行是包容性扫描,因此输出的第一个元素必须扇出给第二个线程束,依此类推。
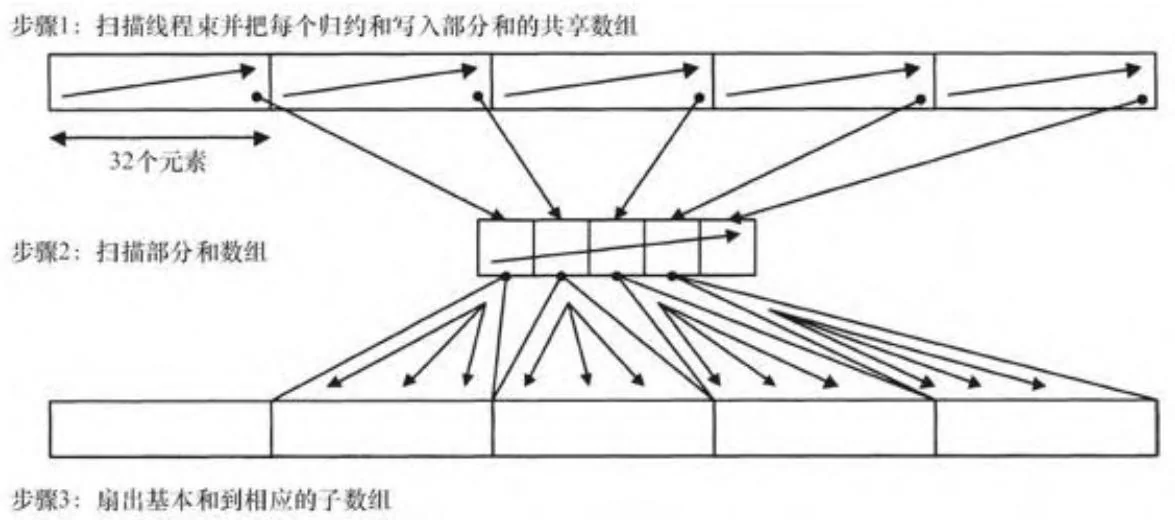
图13-12 先扫描再扇出(共享内存)
实现这个算法的代码如代码清单13-3。假设输入数组已经加载到共享内存并且参数sharedPartials和idx分别指定了待扫描线程束的基地址和索引。(在我们第一次实现的版本,threadIdx.x被作为参数idx传递)。代码的 行实现图13-12中的步骤1; 行实现步骤2; 行实现步骤3。这个线程写回的输出值返回给调用者,但仅当它正好是该线程块的归约时才使用。
代码清单13-3 scanBlock: 针对线程块进行先扫描再扇出的线程块部分
template<class T> inline_device_T scanBlock( volatile T *sPartials) {
extern shared T warpPartials;
const int tid = threadIdx.x;
const int lane = tid & 31;
const int warpid = tid >> 5;
//
// Compute this thread's partial sum
//
T sum = scanWarp<T>(sPartials);
__syncthreads();
//
//Write each warp's reduction to shared memory
//
if (lane == 31) {
warpPartials[16+warpid] = sum;
}
__syncthreads();
//
//Have one warp scan reductions
//
if (warpid == 0) {
scanWarp<T>(16+warparts+tid);
}
__syncthreads();
//
//Fan out the exclusive scan element (obtained by the conditional and the decrement by 1)
//to this warp's pending output
//
if (warpid > 0) {
sum += warpPartials[16+warpid-1];
}
__syncthreads();
//
//Write this thread's scan output
//
*sPartials = sum;
__syncthreads();
//
//The return value will only be used by caller if it contains the spine value (i.e., the reduction of the array we just scanned).
//
return sum;图13-13显示了这种方法是如何应用到全局内存的。一个内核扫描b个元素构成的子数组,这里b是线程块大小。部分和被写入到全局内
存;而另一个仅使用一个块启动的内核扫描这些部分和,然后把它们扇出到全局内存的最终输出。
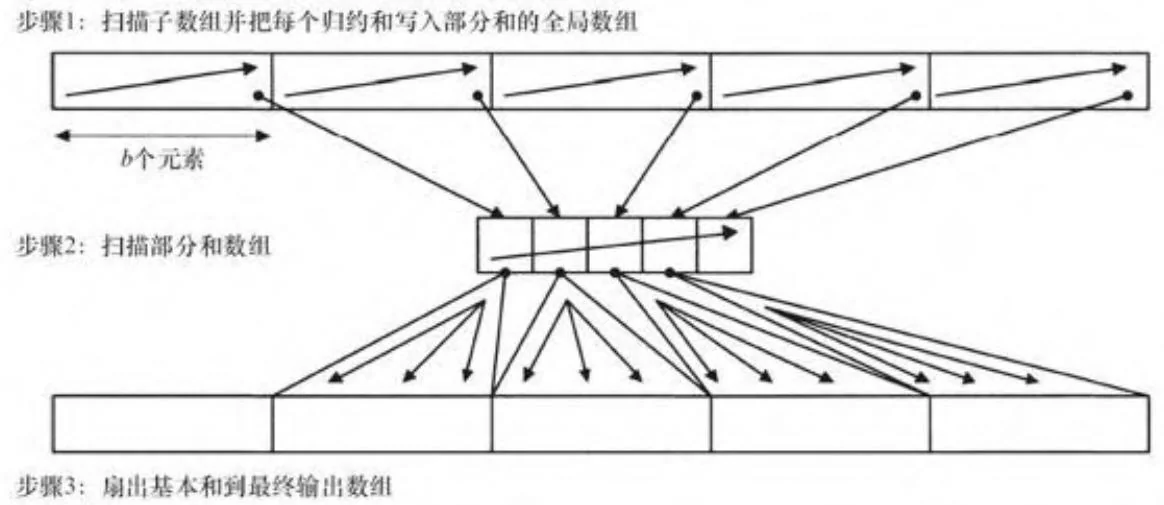
图13-13 先扫描再扇出(全局内存)
代码清单13-4给出了图13-13步骤1中扫描内核的CUDA代码。它遍历全部线程块并进行处理,把输入数组通过共享内存进行中转。然后,内核根据需要,决定是否把脊柱上得到的值最终写回全局内存。在递归的底部,没有必要记录脊柱值,所以bWriteSpine模板参数使内核避免动态检查partialIsOut的值。
代码清单13-4 scanAndWritePartials
template<class T, bool bWriteSpine> global _void
scanAndWritePartials(
T *out,
T *gPartials,
const T *in,
size_t N,
size_t numBlocks)
{
extern volatile __shared__T sPartials[](t);
const int tid = threadIdx.x;
volatile T *myShared = sPartials + tid;
for (size_t iBlock = blockIdx.x; iBlock < numBlocks; iBlock += gridDim.x) {
size_t index = iBlock * blockDim.x + tid;
*myShared = (index < N) ? in[index] : 0;
__syncthreads();
T sum = scanBlock(myShared);
__syncthreads();
if (index < N) {
out[index] = *myShared;
}
// write the spine value to global memory
// if (bWriteSpine && (threadIdx.x == (blockDim.x-1)) {
gPartials[iBlock] = sum;
}
}代码清单13-5给出了一个主机函数,它使用代码清单13-3和13-4来实现来自全局内存上数组的包容性扫描。注意,对于扫描过大无法在共享内存执行的情况,该函数递归的进行扫描。该函数的第一个条件既作为递归的标准条件,也对那些小到可以放入共享内存执行的小电路扫描问题,免去分配全局内存的需要。注意内核所需的共享内存量(b*sizeof(T))是在内核启动时指定的。
对于更大规模的扫描,该函数计算所需的部分和的数目「N/b」、分配全局内存来保存它们并遵循图3-13的模式,把部分和写回到全局数组,以备由后面的scanAndWritePartials内核(见代码清单13-4)使用。
递归的每一层下来,待处理的元素数降低为原来的 ,因此对于 和 的例子中,需要两层递归:1个是大小为8192规模的,另一个是大小为64规模的。
代码清单13-5 scanf主机函数
template<class T>
void
scanFan(T \*out, const T \*in, size_t N, int b)
{udaError_t status; if(N<=b){ scanAndWritePartials<T,false $> < < 1,b,b^{*}$ sizeof(T) $\gg >$ {out,0,in,N,1); return; } // device pointer to array of partial sums in global memory // T\*gPartials $= 0$ . //ceil(N/b) // size_t numPartials $= (N1) / b$ . // number of CUDA threadblocks to use. The kernels are // blocking agnostic, so we can clamp to any number // within CUDA's limits and the code will work. // const unsigned int maxBlocks $= 150$ ;// maximum blocks to launch unsigned int numBlocks $= \min$ (numPartials,maxBlocks); CUDART_CHECK(udaMalloc(&gPartials, numPartials\*sizeof(T))); scanAndWritePartials<T,True><<numBlocks,b,b\*sizeof(T) $\gg >$ out,gPartials,in,N,numPartials); scanFan<T>(gPartials,gPartials,numPartials,b); scanAddBaseSums<T><<numBlocks,b>>>(out,gPartials,N, numPartials); Error: CUDAFree(gPartials);代码清单13-6使用一个简单的内核,把来自全局内存的结果扇出到全局内存,完成整个算法。
代码清单13-6 scanAddBaseSums内核
template<class T> global __void scanAddBaseSums()
{
T *out,
T *gBaseSums,
size_t N,
size_t numBlocks;
}
const int tid = threadIdx.x;
T fan_value = 0;
for (size_t iBlock = blockIdx.x;
iBlock < numBlocks;
iBlock += gridDim.x) {
size_t index = iBlock * blockDim.x + tid;
if (iBlock > 0) {
fan_value = gBaseSums[iBlock - 1];
}
out[index] += fan_value;
}在递归的最高层,先扫描再扇出的策略会执行4N次全局内存操作。初始扫描执行一次读和一次写,然后代码清单13-4的扇出操作执行另一次读和另一次写。我们可以通过首先只计算输入数组的归约来减少全局内存的写入次数。
13.4.2 先归约再扫描(递归)
图13-14显示了这一策略是如何工作的。如前,计算出输入的部分和数组(N/b个元素),并对它进行扫描以获得一个基本和数组。但不是在第一阶段做扫描操作,相反,我们在第一阶段只计算部分和。然后把基本和依次加入,完成最终输出的扫描。
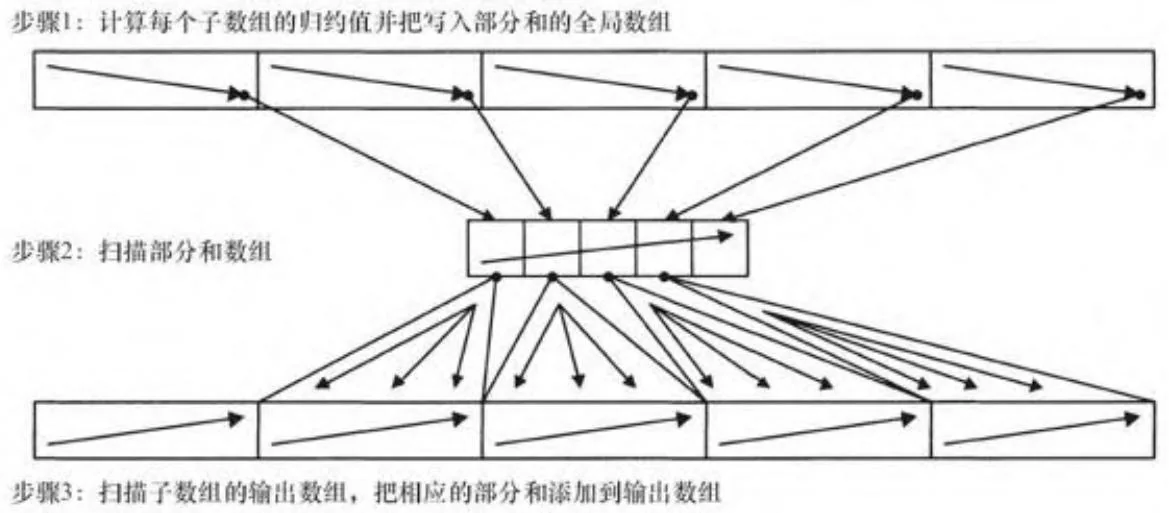
图13-14 先归约再扫描
代码清单13-7给出了用于计算部分和数组的代码,它把来自代码清单12-3的归约代码作为子程序调用。与归约代码一样,内核按照线程块大小进行了模板化处理,并且一个包装模板使用一个switch语句来调用模板的实例。
代码清单13-7 scanReduceBlocks
template<class T, int numThreads> global _void
scanReduceBlocks(T *gPartials, const T *in, size_t N) {
extern volatile __shared__T sPartials[](i);
const int tid = threadIdx.x;
gPartials += blockIdx.x;
for (size_t i = blockIdx.x*blockDim.x;
i < N;
i += blockDim.x*gridDim.x) {
size_t index = i+tid;
sPartials[tid] = (index < N) ? in[index] : 0;
__synchthreads();
reduceBlock<T, numThreads>(gPartials, sPartials);
__synch threads();
gPartials += gridDim.x;
}
}
template<class T> void
scanReduceBlocks(
T *gPartials,
const T *in,
size_t N,
int numThreads,
int numBlocks)
{
switch (numThreads) {
case 128: return scanReduceBlocks<T, 128> ... (...);
case 256: return scanReduceBlocks<T, 256> ... (...);
case 512: return scanReduceBlocks<T, 512> ... (...);
case 1024: return scanReduceBlocks<T, 1024> ... (...);
}代码清单13-8给出了用于执行扫描的内核。与代码清单13-4的主要区别在于,不是把输入子数组之和写入全局内存,相反,内核把每个子数组对应的基本和在写入之前添加于输出元素。
代码清单13-8 scanWithBaseSums
template<class T> global __void
scanWithBaseSums()
T *out,
const T *gBaseSums,
const T *in,
size_t N,size_t numBlocks)
{ extern volatile __shared_T sPartials[]; const int tid $=$ threadIdx.x; for ( size_t iBlock $=$ blockIdx.x; iBlock $<$ numBlocks; iBlock $+ =$ gridDim.x){ T base_sum $= 0$ size_t index $=$ iBlock\*blockDim.x+tid; if(iBlock>0&&gBaseSums){ base_sum $=$ gBaseSums[iBlock-1]; } sPartials[tid] $=$ (index $< \mathbb{N}$ ?in[index]:0; _syncthreads(); scanBlock(sPartials+tid); _syncthreads(); if(index $< \mathbb{N}$ ){ out[index] $=$ sPartials[tid]+base_sum; } }采用先归约再扫描策略的主机代码如代码清单13-9所示。在归约的最高层,先归约后扫描策略进行3N次全局内存操作。归约的第一遍每个元素执行一次读,然后代码清单13-9中的扫描操作执行另一次读和一次写。与先扇出再扫描策略类似,递归的每一层处理的元素数都只是上一层的 。
代码清单13-9 scanReduceThenScan
template<class T>
void
scanReduceThenScan(T \*out, const T \*in, size_t N, int b)
{udaError_t status; if(N<=b){ return scanWithBaseSums<T><<<1,b,b\*sizeof(T) >>>( out,0,in,N,1); // // device pointer to array of partial sums in global memory // T \*gPartials-0; //ceil(N/b) $=$ number of partial sums to compute // size_t numPartials $= (\mathrm{N}1) / \mathrm{b}$ . // number of CUDA threadblocks to use. The kernels are blocking // agnostic, so we can clamp to any number within CUDA's limits // and the code will work. // const unsigned int maxBlocks $= 150$ unsigned int numBlocks $= \min$ (numPartials,maxBlocks); CUDART_CHECK(cudaMalloc(&gPartials,numPartials\*sizeof(T))); scanReduceBlocks<T>(gPartials,in,N,b,numBlocks); scanReduceThenScan<T>(gPartials,gPartials,numPartials,b); scanWithBaseSums<T><<numBlocks,b,b\*sizeof(T) $>> >$ { out, gPartials, in, N, numPartials); Error:udaFree(gPartials); }13.4.3 先归约再扫描(两阶段)
Merrill [2] 描述了另一种扫描方法,使用了少量固定大小的基本和。该算法与图13-14几乎完全相同,不同之处在于步骤2中的数组相对较小,可能只有数百个固定大小而不是「N/b」个部分和构成。不论是在归约阶段还是扫描阶段,部分和的数目与使用的线程块数量相同。代码清单13-10显示了计算这些部分和的代码,它被更新为计算大
小为elementsPerPartial个元素而不是线程块大小个元素的子数组的归约。4
代码清单13-10 scanReduceSubarrays
template<class T, int numThreads>
_device_ void
scanReduceSubarray(
T *gPartials,
const T *in,
size_t iBlock,
size_t N,
int elementsPerPartial()
{
extern volatile __shared__T sPartials[],
const int tid = threadIdx.x;
size_t baseIndex = iBlock*elementsPerPartial;
T sum = 0;
for (int i = tid; i < elementsPerPartial; i += blockDim.x) {
size_t index = baseIndex + i;
if (index < N)
sum += in[index];
}
sPartials[tid] = sum;
__syncthreads();
reduceBlock<T, numThreads>(&gPartials[iBlock], sPartials);
}
/*
* Compute the reductions of each subarray of size
*elementsPerPartial, and write them to gPartials. */
*/
template<class T, int numThreads>
global _void
scanReduceSubarrays(
T *gPartials,
const T *in,
size_t N,
int elementsPerPartial()
{
extern volatile __shared__T sPartials[],
for (int iBlock = blockIdx.x;
iBlock*elementsPerPartial < N;
iBlock += gridDim.x)
{
scanReduceSubarray<T, numThreads>(gPartials,
in,
iBlock,
N,
elementsPerPartial);
}
}
}代码清单13-11提供了扫描代码,已被修改来在一个线程块完成扫描操作后执行对每块中和的扫描操作。代码清单13-11中的bZeroPad模板参数和使用它的scanSharedIndex辅助函数将在13.5.1节予以详描。
代码清单13-11 scan2Level_kernel
template<class T, bool bZeroPad> global _void scan2Level_kernel(
T *out,
const T *gBaseSums,
const T *in,
size_t N,
size_t elementsPerPartial()
{
extern volatile __shared__T sPartials[](int tid = threadIdx.x;
int sIndex = scanSharedIndex<bZeroPad>(threadIdx.x));
if (bZeroPad) {
sPartials[sIndex-16] = 0;
}
T base_sum = 0;
if (blockIdx.x && gBaseSums) {
base_sum = gBaseSums(blockIdx.x-1);
}
for (size_t i = 0; i < elementsPerPartial; i++)
i += blockDim.x) {
size_t index = blockIdx.x*elementsPerPartial + i + tid;
sPartials[sIndex] = (index < N) ? in[index] : 0;
__syncthreads();
scanBlock<T,bZeroPad>(sPartials+sIndex);
__syncthreads();
if (index < N) {
out[index] = sPartials[sIndex] + base_sum;
}
__syncthreads();
// carry forward from this block to the next.
base_sum += sPartials[scanSharedIndex<bZeroPad>(blockDim.x-1)];
__syncthreads();
}代码清单13-12给出了Merrill的两阶段先归约再扫描算法的主机代码。由于计算出的部分和数目很小而且从不改变,主机代码永远不
用为了执行扫描而分配全局内存,相反,我们声明一个在模块加载时分配空间的__device__数组。
device int g_globalPartials [MAX_PARTIALS];并通过调用)cudaGetSymbolAddress()获取其地址。
status $=$ CUDAGetSymbolAddress( (void \*\*)&globalPartials, g_globalPartials);该程序然后计算每个部分和包含的元素数目以及要使用的线程块数目,并调用执行计算所需的3个内核。
代码清单13-12 scan2Level
template<class T, bool bZeroPad> void scan2Level(T *out, const T *in, size_t N, int b) {
int sBytes = scanSharedMemory<T, bZeroPad>(b);
if (N <= b) {
return scan2Level_kernel<T, bZeroPad><<1,b,sBytes>>(out, 0, in, N, N);
}
JudaError_t status;
T *gPartials = 0;
status = JudaGetSymbolAddress(
(void **) &gPartials,
g_globalPartials);
if (CUDASuccess == status)
// // ceil(N/b) = number of partial sums to compute
// size_t numPartials = (N + b - 1)/b;
if (numPartials > MAX_PARTIALS) {
numPartials = MAX_PARTIALS;
}
// elementsPerPartial has to be a multiple of b
unsigned int elementsPerPartial = (N + numPartials - 1)/numPartials;
elementsPerPartial = b * ((elementsPerPartial + b - 1)/b);numPartials $=$ (N+elementsPerPartial-1)/elementsPerPartial;
//
// number of CUDA threadsblocks to use. The kernels are
// blocking agnostic, so we can clamp to any number within
// CUDA's limits and the code will work.
//
const unsigned int maxBlocks $=$ MAX_PARTIALS;
unsigned int numBlocks $=$ min(numPartials,maxBlocks);
scanReduceSubarrays<T>( gPartials, in, N, elementsPerPartial, numBlocks, b);
scan2Level_kernel<T,bZeroPad><<<1,b,sBytes>>>( gPartials, 0, gPartials, numPartials, numPartials);
scan2Level_kernel<T,bZeroPad><<numBlocks,b,sBytes>>>( out, gPartials, in, N, elementsPerPartial);[1] 使用CUDA 5.0和SM 3.5硬件,动态并行可以将多数内核启动转移到“子网格”,而不是由主机发起的内核启动。
[2] http://bit.ly/ZKtlh1。