8._相关系数

相关系数的通俗解释

问题:考试砸了回到家，母亲打我的概率是 1/2，父亲打我的概率也是 1/2，那我被打的概率是多少

解答：你被打的概率与你爸妈行为之间的相关性密不可分。首先，为了建模，我们适当地对问题做以下简化假设：（1）仅关注挨打与否的概率，而暂不关注挨打的强度。也即只关注打没打，暂不关注挨几顿打，毕竟自己爸妈嘛，应该不至于往死里打。（2）假设你爸妈的行为之间仅存在线性相关性，而不存在复杂的非线性相关关系。线性相关程度则可通过相关性系数来描述。

记你挨打的概率为$P$，你爸妈行为之间的相关性系数为$\rho$

我们先看三种特殊ρ值的情况。

（1）假设 $\rho=0$ ，也即你爸是否打你和你妈是否打你两个随机变量 之间不存在线性相关性，由于我们先假设了两者之间不存在复杂的非线性相关关系，因此可以认为两者相互独立，那么问题其实就等价于＂抛两次硬币，求抛出至少一次反面的概率＂。显然地，你被打的概率等于 1 减去你不被打的概率，也即 $1-1 / 2^* 1 / 2=3 / 4$ ，也即 $75 \%$ 。 （2）假设 $\rho=1$ ，也即你爸妈的行为完全正相关，也就是完全趋同。如果其中一个打你，另外一个也会一起打你。如果其中一个放过你，另外一个也放过你。那么你被打的概率是 $1 / 2$ ，也即 $50 \%$ 。

（3）假设 $p=-1$ ，也即假设你爸妈的行为完全负相关，也就是完全反着来。如果其中一个打你，另外一个选择放过你。如果其中一个选择放过你，另外一个就一定打你。那么很遗憾，你被打的概率是 1，也即 $100 \%$ 。

假设 p 取 $[-1,1]$ 区间的其它值，就需要有 $P$ 关于 $\rho$ 的表达式，推理稍微有些复杂。但由于概率 $P$ 和相关性 $\rho$ 之间的线性关系（严格来说需要证明），而且根据上面三种特殊情况，已经明确的知道了直线上三个特殊点的坐标分别为 $(0,0.75)$ ，$(1,0.5)$ ，$(-1,1)$ 。通过其中任意两点可以推出 $P$ 关于 $\rho$ 的线性关系式为 $P=0.75-0.25 \rho$ 。

由于 $\rho$ 的取值范围是 $[-1,1]$ ，易得出概率 $P$ 的取值范围是 $[0.5,1]$ 区间。整体趋势而言是你爸妈的行为越趋同，你被打的概率越低。行为越趋反，你挨打的概率越高。

如果你爸妈平时感情很好总是夫唱妇随的话，你勇敢进家门就好了，好歹有约一半的概率不被打（当然也有约一半的概率遭遇男女混合双打）。如果他俩喜欢唱反调，或者总是喜欢红脸黑脸地演戏，你看下今晚能不能去爷爷奶奶家或者同学家借住一宿，但尽量别去网吧通宵。

相关系数的定义与性质

定义 设 $(X, Y)$ 为二维随机变量，$D(X)>0, D(Y)>0$ ，称

为随机变量 $X$ 和 $Y$ 的相关系数（Correlation Coefficient）或标准协方差（Standard Covariance）。记为 $\rho_{X Y}$ ，即

在不引起混淆的情况下，有时也记 $\rho_{X Y}$ 为 $\rho$ 。 下面给出相关系数 $\rho_{X Y}$ 的几条重要性质，并说明 $\rho_{X Y}$ 的含义．

性质1 $\left|\rho_{X Y}\right| \leqslant 1$ ． 性质2 若 $X$ 和 $Y$ 相互独立，则 $\rho_{X Y}=0$ ． 性质3 $\left|\rho_{X Y}\right|=1$ 的充要条件是存在常数 $a, b(a \neq 0)$ ，使 $P\{Y=a X+b\}=1$ ，而且当 $a>0$时，$\rho_{X Y}=1$ ；当 $a<0$ 时，$\rho_{X Y}=-1$ ．

由协方差的性质及相关系数的定义可知性质2 成立，性质3 的证明较复杂，从略．下面仅证明性质1．

证明 对任意实数 $t$ ，有

令 $t=\frac{\operatorname{Cov}(X, Y)}{D(X)}=b$ ，于是

由于方差不能为负，所以 $1-\rho_{X Y}^2 \geqslant 0$ ，从而 $\left|\rho_{X Y}\right| \leqslant 1$ ．

注意：相关系数 $\rho_{X Y}$ 刻画了随机变量 $Y$ 与 $X$ 之间的＂线性相关＂程度．$\left|\rho_{X Y}\right|$ 的值越接近 $1, Y$ 与 $X$ 的线性相关程度越高；$\left|\rho_{X Y}\right|$ 的值越接近 $0, Y$ 与 $X$ 的线性相关程度越弱。当 $\left|\rho_{X Y}\right|=1$时，$Y$ 与 $X$ 的变化可完全由 $X$ 的线性函数给出，即 $X$ 与 $Y$ 存在着完全线性关系，是一种极端情况；当 $\rho=1$ 时，称为完全正相关；当 $\rho=-1$ 时，称为完全负相关；当 $\rho_{X Y}=0$ 时，$Y$ 与 $X$之间不是线性关系，是另一种极端情况。

当 $\rho_{X Y}=0$ 时，称 $X$ 与 $Y$ 不相关，由性质 4．3．2 可知，当 $X$ 与 $Y$ 相互独立时，$\rho_{X Y}=0$ ，即称 $X$ 与 $Y$ 不相关．反之，成立否？

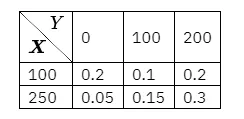
例 设保险公司对投保人的汽车保险和财产保险分别设定了免赔额（单位：元），现任选一位同时投保汽车保险和财产保险的客户，$X$ 表示其汽车保单的免赔额，$Y$ 表示其财产保单的免赔额，随机变量 $(X, Y)$ 的联合分布律如下。 求 $\operatorname{cov}(X, Y)$ 和 $\rho_{X Y}$ ． 解：由联合分布律，可得随机变量 $X, Y$ 的分布律如下．

同理

又

故

例 已知 $D(X)=4, D(Y)=1, \rho_{X Y}=0.5$ ，求 $D(3 X-2 Y)$ ． 解 由方差、协方差的性质及相关系数的定义可得

例设 $\theta$ 服从 $[-\pi, \pi]$ 上的均匀分布，$X=\sin \theta, Y=\cos \theta$ ．判断 $X$ 与 $Y$ 是否不相关，是否独立。

解 由于 $E(X)=\frac{1}{2 \pi} \int_{-\pi}^\pi \sin \theta d \theta=0, E(Y)=\frac{1}{2 \pi} \int_{-\pi}^\pi \cos \theta d \theta=0$ ， 而 $E(X Y)=\frac{1}{2 \pi} \int_{-\pi}^\pi \sin \theta \cos \theta d \theta=0$ ． 因此 $\rho_{X Y}=\frac{\operatorname{Cov}(X, Y)}{\sqrt{D(X) D(Y)}}=\frac{E(X Y)-E(X) E(Y)}{\sqrt{D(X) D(Y)}}=0$ ，从而 $X$ 与 $Y$ 不相关。但由于 $X$ 与 $Y$ 满足关系 $X^2+Y^2=1$ ，所以 $X$ 与 $Y$ 不独立．

注意：当两个随机变量不相关时，它们并不一定相互独立，它们之间还可能存在其他的函数关系．

例 设二维随机变量 $(X, Y) \sim N\left(\mu_1, \mu_2, \sigma_1, \sigma_2, \rho\right)$ ，求相关系数 $\rho_{X Y}$ ． 解 根据二维正态分布的边缘概率密度知

而

令 $t=\frac{1}{\sqrt{1-\rho^2}}\left(\frac{y-\mu_2}{\sigma_2}-\rho \frac{x-\mu_1}{\sigma_1}\right), u=\frac{x-\mu_1}{\sigma_1}$ ，则有

即有 $\operatorname{Cov}(X, Y)=\rho \sigma_1 \sigma_2$ ，于是 $\rho_{X Y}=\frac{\operatorname{Cov}(X, Y)}{\sqrt{D(X)} \sqrt{D(Y)}}=\rho$ ． 注意：从本例的结果可见，二维正态随机变量 $(X, Y)$ 的分布完全由 $X$ 和 $Y$ 各自的数学期望、方差及它们的相关系数所确定. 此外，易见有结论：若( , ) XY服从二维正态分布，则X与Y相互独立，当且仅当X与Y不相关.