7._协方差

在前两节中，我们介绍了一维随机变量的数字特征．对于二维随机变量 (X,Y)(X, Y) ，除了讨论随机变量 XX 和 YY 各自的数学期望和方差，还需要研究描述 XX 与 YY 之间相互关系的数字特征。例如，假设某品牌企业的广告支出 XX 和销售收入 YY 都为随机变量，XX 和 YY 往往是不独立的，需要分析 XX 与 YY 之间的依赖关系，即相关性．本节介绍的协方差和相关系数就是用来描述 XX 与 YY 之间相互关系的数字特征．

协方差定义

定义 设二维随机变量 (X,Y)(X, Y) ，若 E{[X−E(X)][Y−E(Y)]}E\{[X-E(X)][Y-E(Y)]\} 存在，则称它为随机变量 XX 与 YY 的协方差，记为 cov⁡(X,Y)\operatorname{cov}(X, Y) ，或 σXY\sigma_{X Y} ，即

cov⁡(X,Y)=E{[X−E(X)][Y−E(Y)]}\operatorname{cov}(X, Y)=E\{[X-E(X)][Y-E(Y)]\}

当 D(X)>0,D(Y)>0D(X)>0, D(Y)>0 时，

ρXY=cov⁡(X,Y)D(X)D(Y)\rho_{X Y}=\frac{\operatorname{cov}(X, Y)}{\sqrt{D(X)} \sqrt{D(Y)}}

称为随机变量 XX 与 YY 的相关系数． 当 ρXY=0\rho_{X Y}=0 时，称随机变量 XX 与 YY 不相关或线性无关． 将随机变量 XX 与 YY 标准化，得

X∗=X−E(X)D(X),Y∗=Y−E(Y)D(Y)X^*=\frac{X-E(X)}{\sqrt{D(X)}}, Y^*=\frac{Y-E(Y)}{\sqrt{D(Y)}}

由相关系数的定义，显然有 ρXY=cov⁡(X∗,Y∗)\rho_{X Y}=\operatorname{cov}\left(X^*, Y^*\right) ． 在实际应用当中，协方差和相关系数是用来描述随机变量 XX 与 YY 之间线性相关方向和依赖程度的数字特征。

由协方差定义及数学期望的性质，可得协方差的计算公式

cov⁡(X,Y)=E(XY)−E(X)E(Y)\operatorname{cov}(X, Y)=E(X Y)-E(X) E(Y)

离散型

若 (X,Y)(X, Y) 为离散型随机向量，其概率分布为

P{X=xi,Y=yj}=piji,j=1,2,⋯ ,P\left\{X=x_i, Y=y_j\right\}=p_{i j} \quad i, j=1,2, \cdots,

则

Cov⁡(X,Y)=∑i∑j[xi−E(X)][yj−E(Y)]pij\operatorname{Cov}(X, Y)=\sum_i \sum_j\left[x_i-E(X)\right]\left[y_j-E(Y)\right] p_{i j}

连续型 若 (X,Y)(X, Y) 为连续型随机向量，其概率分布为 f(x,y)f(x, y) ，则

Cov⁡(X,Y)=∫−∞+∞∫−∞+∞{[x−E(X)][y−E(Y)]}f(x,y)dxdy\operatorname{Cov}(X, Y)=\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty}\{[x-E(X)][y-E(Y)]\} f(x, y) d x d y

此外，由协方差定义和数学期望的性质可得以下有用的计算公式

Cov⁡(X,Y)=E{[X−E(X)][Y−E(Y)]}=E(XY)−E(X)E(Y)−E(Y)E(X)+E(X)E(Y)=E(XY)−E(X)E(Y)\begin{aligned} \operatorname{Cov}(X, Y) & =E\{[X-E(X)][Y-E(Y)]\} \\ & =E(X Y)-E(X) E(Y)-E(Y) E(X)+E(X) E(Y) \\ & =E(X Y)-E(X) E(Y) \end{aligned}

特别地，当 XX 与 YY 独立时，有 Cov⁡(X,Y)=0\operatorname{Cov}(X, Y)=0 ．

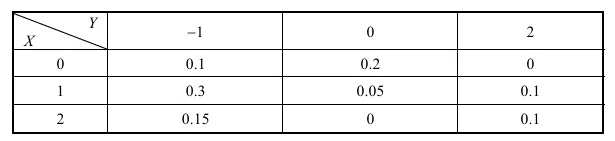
例 已知离散型随机向量( X,Y ) 的概率分布为 图片

求 Cov⁡(X,Y)\operatorname{Cov}(X, Y) ． 解 容易求得 XX 的概率分布为 P{X=0}=0.3,P{X=1}=0.45,P{X=2}=0.25P\{X=0\}=0.3, P\{X=1\}=0.45, P\{X=2\}=0.25 ； YY 的概率分布为 P{Y=−1}=0.55,P{Y=0}=0.25,P{Y=2}=0.2P\{Y=-1\}=0.55, P\{Y=0\}=0.25, P\{Y=2\}=0.2 ， 于是有

E(X)=0×0.3+1×0.45+2×0.25=0.95E(Y)=(−1)×0.55+0×0.25+2×0.2=−0.15\begin{gathered} E(X)=0 \times 0.3+1 \times 0.45+2 \times 0.25=0.95 \\ E(Y)=(-1) \times 0.55+0 \times 0.25+2 \times 0.2=-0.15 \end{gathered}

计算得 E(XY)=0×(−1)×0.1+0×0×0.2+0×2×0+1×(−1)×0.3+1×0×0.5+1×2×0.1+E(X Y)=0 \times(-1) \times 0.1+0 \times 0 \times 0.2+0 \times 2 \times 0+1 \times(-1) \times 0.3+1 \times 0 \times 0.5+1 \times 2 \times 0.1+

2×(−1)×0.15+2×0×0+2×2×0.1=0.2 \times(-1) \times 0.15+2 \times 0 \times 0+2 \times 2 \times 0.1=0 .

于是

Cov⁡(X,Y)=E(XY)−E(X)E(Y)=0.95×0.15=0.1425.\operatorname{Cov}(X, Y)=E(X Y)-E(X) E(Y)=0.95 \times 0.15=0.1425 .

例 设 (X,Y)(X, Y) 的概率密度为

f(x,y)={x+y,0<x<1,0<y<10, 其他 , f(x, y)=\left\{\begin{array}{ll} x+y, & 0<x<1,0<y<1 \\ 0, & \text { 其他 } \end{array}\right. \text {, }

求 Cov⁡(X,Y)\operatorname{Cov}(X, Y) ． 解 由于 fX(x)={x+12,0<x<10, 其他 ,fY(y)={y+12,0<y<10, 其他 f_X(x)=\left\{\begin{array}{ll}x+\frac{1}{2}, & 0<x<1 \\ 0, & \text { 其他 }\end{array}, \quad f_Y(y)=\left\{\begin{array}{ll}y+\frac{1}{2}, & 0<y<1 \\ 0, & \text { 其他 }\end{array}\right.\right. ，

E(X)=∫01x(x+12)dx=712E(X)=\int_0^1 x\left(x+\frac{1}{2}\right) d x=\frac{7}{12}
E(Y)=∫01y(y+12)dy=712E(XY)=∫01∫01xy(x+y)dxdy=∫01∫01x2ydxdy+∫01∫01xy2dxdy=13Cov⁡(X,Y)=E(XY)−E(X)E(Y)=13−712×712=−1144\begin{gathered} E(Y)=\int_0^1 y\left(y+\frac{1}{2}\right) d y=\frac{7}{12} \\ E(X Y)=\int_0^1 \int_0^1 x y(x+y) d x d y=\int_0^1 \int_0^1 x^2 y d x d y+\int_0^1 \int_0^1 x y^2 d x d y=\frac{1}{3} \\ \operatorname{Cov}(X, Y)=E(X Y)-E(X) E(Y)=\frac{1}{3}-\frac{7}{12} \times \frac{7}{12}=-\frac{1}{144} \end{gathered}

因此

协方差的性质

定理 设随机变量 X、YX 、 Y 的方差存在，则 （1） Cov⁡(X,X)=D(X)\operatorname{Cov}(X, X)=D(X) ； （2） Cov⁡(X,Y)=Cov⁡(Y,X)\operatorname{Cov}(X, Y)=\operatorname{Cov}(Y, X) ； （3） Cov⁡(aX,bY)=abCov⁡(X,Y)\operatorname{Cov}(a X, b Y)=a b \operatorname{Cov}(X, Y) ，其中 a、ba 、 b 是常数； （4） Cov⁡(C,X)=0,C\operatorname{Cov}(C, X)=0, C 为任意常数； （5） Cov⁡(X1+X2,Y)=Cov⁡(X1,Y)+Cov⁡(X2,Y)\operatorname{Cov}\left(X_1+X_2, Y\right)=\operatorname{Cov}\left(X_1, Y\right)+\operatorname{Cov}\left(X_2, Y\right) ； （6）当 XX 与 YY 相互独立时，则 Cov⁡(X,Y)=0\operatorname{Cov}(X, Y)=0 ； （7）D(X+Y)=D(X)+D(Y)+2Cov⁡(X,Y)D(X+Y)=D(X)+D(Y)+2 \operatorname{Cov}(X, Y) ． 特别地，若 XX 与 YY 相互独立时，则

D(X+Y)=D(X)+D(Y).D(X+Y)=D(X)+D(Y) .

证明 仅证性质（5）

Cov⁡(X1+X2,Y)=E[(X1+X2)Y]−E(X1+X2)E(Y)=E(X1Y)+E(X2Y)−E(X1)E(Y)−E(X2)E(Y)=[E(X1Y)−E(X1)E(Y)]+[E(X2Y)−E(X2)E(Y)]=Cov⁡(X1,Y)+Cov⁡(X2,Y)\begin{aligned} \operatorname{Cov}\left(X_1+X_2, Y\right) & =E\left[\left(X_1+X_2\right) Y\right]-E\left(X_1+X_2\right) E(Y) \\ & =E\left(X_1 Y\right)+E\left(X_2 Y\right)-E\left(X_1\right) E(Y)-E\left(X_2\right) E(Y) \\ & =\left[E\left(X_1 Y\right)-E\left(X_1\right) E(Y)\right]+\left[E\left(X_2 Y\right)-E\left(X_2\right) E(Y)\right] \\ & =\operatorname{Cov}\left(X_1, Y\right)+\operatorname{Cov}\left(X_2, Y\right) \end{aligned}

例 设连续型随机变量 (X,Y)(X, Y) 的密度函数为

f(x,y)={8xy,0⩽x⩽y⩽10, 其他 , f(x, y)=\left\{\begin{array}{ll} 8 x y, & 0 \leqslant x \leqslant y \leqslant 1 \\ 0, & \text { 其他 } \end{array}\right. \text {, }

求 Cov⁡(X,Y)\operatorname{Cov}(X, Y) 和 D(X+Y)D(X+Y) ． 解 由 (X,Y)(X, Y) 的密度函数可求得其边缘密度函数分别为

fX(x)={4x(1−x2),0⩽x⩽10, 其他 ,fY(y)={4y3,0⩽y⩽10, 其他 , f_X(x)=\left\{\begin{array}{ll} 4 x\left(1-x^2\right), & 0 \leqslant x \leqslant 1 \\ 0, & \text { 其他 } \end{array}, \quad f_Y(y)=\left\{\begin{array}{ll} 4 y^3, & 0 \leqslant y \leqslant 1 \\ 0, & \text { 其他 } \end{array}\right. \text {, }\right.

于是

E(X)=∫−∞+∞xfX(x)dx=∫01x⋅4x(1−x2)dx=8/15E(Y)=∫−∞+∞yfY(y)dy=∫01y⋅4y3dy=4/5E(XY)=∫−∞+∞∫−∞+∞xyf(x,y)dxdy=∫01dx∫x1xy⋅8xy⋅dy=4/9\begin{gathered} E(X)=\int_{-\infty}^{+\infty} x f_X(x) d x=\int_0^1 x \cdot 4 x\left(1-x^2\right) d x=8 / 15 \\ E(Y)=\int_{-\infty}^{+\infty} y f_Y(y) d y=\int_0^1 y \cdot 4 y^3 d y=4 / 5 \\ E(X Y)=\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} x y f(x, y) d x d y=\int_0^1 d x \int_x^1 x y \cdot 8 x y \cdot d y=4 / 9 \end{gathered}

从而

Cov⁡(X,Y)=E(XY)−E(X)E(Y)=4/225,\operatorname{Cov}(X, Y)=E(X Y)-E(X) E(Y)=4 / 225,

又

E(X2)=∫−∞+∞x2fX(x)dx=∫01x2⋅4x(1−x2)dx=1/3E\left(X^2\right)=\int_{-\infty}^{+\infty} x^2 f_X(x) d x=\int_0^1 x^2 \cdot 4 x\left(1-x^2\right) d x=1 / 3
E(Y2)=∫−∞+∞y2fY(y)dy=∫01y2⋅4y3dy=2/3E\left(Y^2\right)=\int_{-\infty}^{+\infty} y^2 f_Y(y) d y=\int_0^1 y^2 \cdot 4 y^3 d y=2 / 3

所以

D(X)=E(X2)−[E(X)]2=11/225,D(Y)=E(Y2)−[E(Y)]2=2/75D(X)=E\left(X^2\right)-[E(X)]^2=11 / 225, D(Y)=E\left(Y^2\right)-[E(Y)]^2=2 / 75

故

D(X+Y)=D(X)+D(Y)+2Cov⁡(X,Y)=1/9D(X+Y)=D(X)+D(Y)+2 \operatorname{Cov}(X, Y)=1 / 9
上一章6._方差的性质
下一章8._相关系数
7._协方差 - 概率论与数理统计 | OpenTech