12._二维相互独立性

在多维随机变量中，各分量的取值有时会相互影响，但有时会毫无影响. 比如一个人的身高和体重会相互影响，但是与收入一般无影响. 当两个随机变量的取值相互不影响时，就称它们是相互独立的.

随机变量的相互独立性

设 $(X, Y)$ 为二维随机变量，若对任意的 $x, y \in R$ 都有$F(x, y)=F_X(x) F_Y(y)$ 成立，则称随机变量$X$ 与 $Y$ 相互独立.

定理 1

设 $(X, Y)$ 为二维离散型随机变量，那么， $X$ 与 $Y$ 相互独立的充分必要条件是对任意的 $i, j=1,2, \cdots$, 都有 $p_{i j}=p_{i \cdot} \times p_{. j}$ 成立.

定理 2

设 $(X, Y)$ 为二维连续型随机变量，那么， $X$ 与 $Y$ 相互独立的充分必要条件是在 $f(x, y), f_X(x)$ 及 $f_Y(y)$ 的一切公共连续点上都有 $f(x, y)=f_X(x) f_Y(y)$

例设二维随机变量 $(X, Y)$ 的联合分布律为

（1）求 $X$ 的边缘与 $Y$ 的边缘分布律； （2）$X$ 与 $Y$ 是否相互独立，为什么？

解：（1）由二维离散型随机变量边缘分布律定义得

所以 $X$ 与 $Y$ 的边缘分布律分别为

（2）可以验证对任意的 $i, j=1,2$ 都有 $p_{i j}=p_{i t} p_{i t}$ ，所以 $X$ 与 $Y$ 相互独立。

例 设 $X$ 与 $Y$ 的联合概率分布为

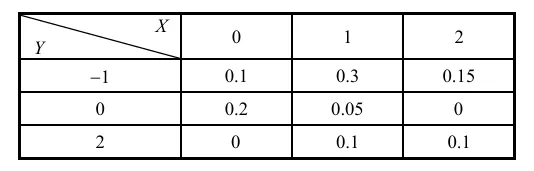
（1）求当 $Y=0$ 时，$X$ 的条件概率分布，以及当 $X=0$ 时，$Y$ 的条件概率分布； （2）判断 $X$ 与 $Y$ 是否相互独立． 解（1）$P(Y=0)=0.2+0.05+0=0.25$ ， 当 $Y=0$ 时，$X$ 的条件概率分布为

又 $P(X=0)=0.1+0.2+0=0.3$ ，故当 $X=0$ 时，$Y$ 的条件概率分布为

（2）因 $P(X=0)=0.1+0.2+0=0.3, P(Y=-1)=0.1+0.3+0.15=0.55$ ，而 $P(X=0, Y=-1)=$ 0.1 ，即 $P(X=0, Y=-1) \neq P(X=0) P(Y=-1)$ ，所以，$X$ 与 $Y$ 不独立．

例 设 $(X, Y)$ 服从单位圆上的均匀分布

问 $X$ 与 $Y$ 是否相互独立？

解 $(X, Y)$ 的联合分布密度为

由此可得

可见在单位圆 $x^2+y^2 \leqslant 1$ 上，$f(x, y) \neq f_X(x) \cdot f_Y(y)$ ，故 $X$ 和 $Y$ 不相互独立．

例 证明 $(X, Y) \sim N\left(\mu_1, \mu_2, \sigma_1^2, \sigma_2^2, \rho\right)$ ，那么 $X$ 与 $Y$ 相互独立的充分必要条件是 $\rho=0$ 证明 充分条件 当 $\rho=0$ 时 所以，对任意 $x, y \in R$ ， 都有 $f(x, y)=f_X(x) f_Y(y)$ 因此 $X$ 与 $Y$ 相互独立. 必要条件 当 $X$ 与 $Y$ 相互独立时，对任意的 $x, y \in R$ 都有

特别地，当 $x=\mu_1, y=\mu_2$ 时 该等式也成立， 所以

n维独立性定义

设 $\left(X_1, X_2, \cdots, X_n\right)$ 为 $n$ 维随机变量，若对任意的 $\left(x_1, x_2, \cdots, x_n\right) \in R^n$ 都有 $F\left(x_1, \ldots, x_n\right)=\prod_{i=1}^n F_{X_i}\left(x_i\right),-\infty<x_1, \ldots, x_n<\infty$ 那么就称随机变量 $\left(X_1, X_2, \cdots, X_n\right)$ 相互独立。连续型随机变量有 $f\left(x_1, \ldots, x_n\right)=\prod_{i=1}^n f_{X_i}\left(x_i\right)$, 在 $f\left(x_1, \cdots, x_n\right), f_{X_1}\left(x_1\right), \cdots, f_{X_n}\left(x_n\right)$ 的一切公共连续点上成立。 当 $\left(X_1, X_2, \cdots, X_n\right)$ 为离散型随机变量 时，随机变量 $X_1, X_2, \cdots, X_n$ 相互独立的充要条件是对任意的 $x_i \in \Omega_{X_i} i=1,2, \cdots, n_1$, 都有 $P\left(X_1=x_1, \cdots, X_n=x_n\right)=\prod_{i=1}^n P\left(X_i=x_i\right)$ 成立.

当 $\left(X_1, X_2, \cdots, X_n\right.$ 为连续型随机变量 时，随机变量 $X_1, X_2, \cdots, X_n$ 相互独立的充要条件是在 $f\left(x_1, x_2, \cdots, x_n\right), f_{X_1}\left(x_1\right), f_{X_2}\left(x_2\right), \cdots, f_{X_n}\left(x_n\right)$ 的一切公共连续点处都有 $f\left(x_1, x_2, \cdots, x_n\right)=\prod_{i=1}^n f_{X_i}\left(x_i\right)$

例 设二维随机变量 $(X, Y)$ 的联合概率密度函数为

证明 $X$ 与 $Y$ 不独立，但 $X^2$ 与 $Y^2$ 独立． 证 对 $X, Y$ 而言：

因为 $f(x, y) \neq f_X(x) f_Y(y)$ ，所以 $X, Y$ 不独立．

而

$U=X^2, V=Y^2$ 的联合分布函数为