在实际生活中,很多变量受到两个或两个以上随机变量的影响。例如,导体的电阻公式为 R=ρL/S ,电阻率 ρ 是常数,电阻受到长度 L 和横截面积 S 的影响;直角三角形的斜边长为 c=a2+b2 ,即斜边长是两个直角边长的函数;某汽车公司生产 3 种型号的汽车,公司总收入是这 3 种汽车产量的函数。这些例子在实际生活中还有很多,因此,研究多维随机变量函数的分布有一定的应用价值.
二维离散型随机变量函数的分布
设 (X,Y) 是二维离散型随机变量,则 Z=g(X,Y) 作为 (X,Y) 的函数仍然是一个离散型随机变量.若 (X,Y) 的概率分布为
P(X=xi,Y=yj)=pij,i,j=1,2,⋯ 且 Z=g(X,Y) 的所有可能取值为 zk,k=1,2,⋯ ,则 Z 的概率分布为
P(Z=zk)=P(g(X,Y)=zk)=g(xi,yj)=zk∑P(X=xi,Y=yj),k=1,2,⋯. 例 设(X,Y)的分布列为
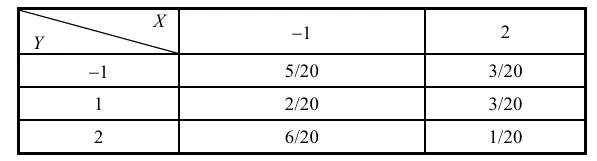 求 Z=X+Y 和 Z=XY的分布列.
解 先列出下表
求 Z=X+Y 和 Z=XY的分布列.
解 先列出下表

从表中看出 Z=X+Y 的可能取值为 −2, 0, 1, 3, 4 ,且
P(Z=−2)=P(X+Y=−2)=P(X=−1,Y=−1)=5/20;P(Z=0)=P(X+Y=0)=P(X=−1,Y=1)=2/20;P(Z=1)=P(X+Y=1)=P(X=−1,Y=2)+P(X=2,Y=−1)=9/20;P(Z=3)=P(X+Y=3)=P(X=2,Y=1)=3/20;P(Z=3)=P(X+Y=4)=P(X=2,Y=2)=1/20. 于是 Z=X+Y 的分布列为
 同理可得,Z=XY 的分布列为
同理可得,Z=XY 的分布列为

从以上两个例题可以看出,求二维离散型随机变量函数的分布律的方法与求一维离散型随机变量函数的分布律是一样的:首先确定所有可能的取值,其次分别求出所有取值的概率,再进行整理便得到了随机变量函数的分布律.
例 设(X,Y)的概率分布为
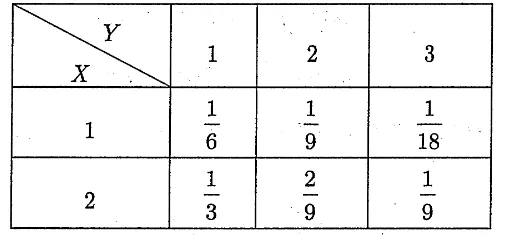 (1)求 U=max{X,Y} 的概率分布;
(2)求 V=min{X,Y} 的概率分布;
(3)求 Z=X+Y 的概率分布.
(1)求 U=max{X,Y} 的概率分布;
(2)求 V=min{X,Y} 的概率分布;
(3)求 Z=X+Y 的概率分布.
解(1) U=max(X,Y) 的概率分布为
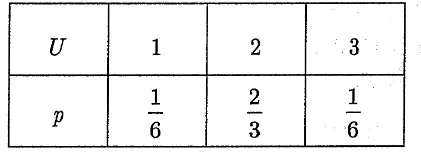
(2)所以 V=min(X,Y) 的概率分布为

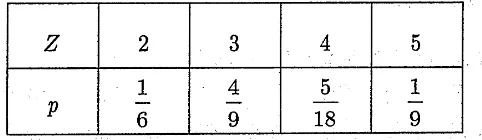
(3)所以Z=X+Y的概率分布为
 求 和 的分布列.
解 先列出下表
求 和 的分布列.
解 先列出下表

 同理可得, 的分布列为
同理可得, 的分布列为
 (1)求 的概率分布;
(2)求 的概率分布;
(3)求 的概率分布.
(1)求 的概率分布;
(2)求 的概率分布;
(3)求 的概率分布.

