二维连续型随机变量的边缘密度函数
设 (X,Y) 是二维连续型随机变量, 其概率密度为 f(x,y), 由定义可得 X 的边缘分布函数
FX(x)=P(X⩽x)=P(X⩽x,y<+∞)=∫−∞x∫−∞+∞f(s,t)dsdt=∫−∞x[∫−∞+∞f(s,t)dt]ds. 进而可得 X 的边缘密度函数为
fX(x)=dxdFX(x)=∫−∞+∞f(x,y)dy. 同理, Y 是连续型随机变量, 且其边缘密度函数为
fY(y)=∫−∞+∞f(x,y)dx. 分别称 fX(x) 和 fY(y) 为 (X,Y) 关于 X 和 Y 的边缘分布密度或边缘概率密度.
设随机变量 X 和 Y 具有联合概率密度
f(x,y)={6,0,x2⩽y⩽x 其他 . 例 一家银行的服务包括人工服务和自助服务.在一天中,X 表示接受人工服务所花费的时间,Y 表示自助服务所花费的时间.二维随机变量 (X,Y) 所有可能取值的集合为 D={(x,y)∣0⩽x⩽1,0⩽y⩽1}(单位: h),(X,Y) 的联合概率密度为
f(x,y)={56(x+y2),0,0⩽x⩽1,0⩽y⩽1, 其他. 求人工服务和自助服务的时间均不超过一刻钟的概率,即求 P{0⩽X⩽41,0⩽Y⩽41} .
解
P{0⩽X⩽41,0⩽Y⩽41}=∫041∫04156(x+y2)dx dy=56∫041∫041x dx dy+56∫041∫041y2 dx dy=206×2x2041+206×3y3041=6407≈0.01 因此,人工服务和自助服务的时间均不超过一刻钟的概率约为 0.01 ,这个概率是非常小的.
例求边缘概率密度 fX(x) 和 fY(y).
解
fX(x)=∫−∞+∞f(x,y)dy={∫x2x6dy=6(x−x2),0,0⩽x⩽1 其他 ,fY(y)=∫−∞+∞f(x,y)dx={∫yy6dx=6(y−y),0,0⩽y⩽1 其他 . 

定理1
设 (X,Y)∼N(μ1,μ2,σ12,σ22,ρ) ,则 X∼N(μ1,σ12),Y∼N(μ2,σ22).
证明 ΩX=ΩY=(−∞,+∞) , 由边缘密度函数的定义得
fx(x)=∫−∞+∞f(x,y)dy=∫−∞+∞2πσ1σ21−ρ21exp{−2(1−ρ2)1[σ12(x−μ1)2−2ρσ1σ2(x−μ1)(y−μ2)+σ22(y−μ2)2]}dy=2πσ11e−2u2⋅∫−∞∞2π1−ρ21exp{−2(1−ρ2)(v−ρu)2}dv=2πσ11e−2σ2(x−μ)2 上面例子说明,如果X,Y服从正态分布,那么X和Y都服从正态分布。

例 设 (X,Y) 在区域 G={(x,y)∣0≤x≤2,0≤y≤1} 上服从均匀分布,令
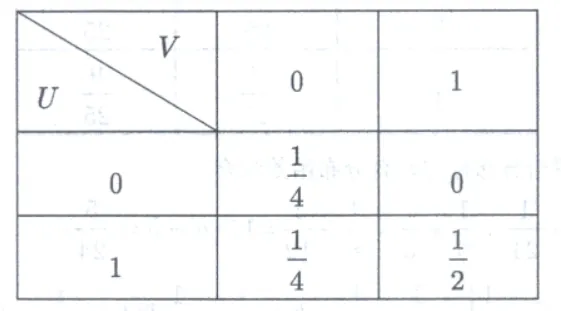
U={0,X≤Y,1,X>Y.V={0,X≤2Y1,X>2Y 求 (U,V) 的联合分布律.
解 由于 (X,Y) 在 G 上服从均匀分布,因此 (X,Y) 的联合概率密度为
f(x,y)={21,0,(x,y)∈G, 其他 P{U=0,V=0}=P{X≤Y,X≤2Y}=P{X≤Y}=∫01dy∫0y21dx=41P{U=0,V=1}=P{X≤Y,X>2Y}=0P{U=1,V=0}=P{X>Y,X≤2Y}=P{Y<X≤2Y}=∫01dy∫y2y21dx=41P{U=1,V=1}=P{X>Y,X>2Y}=P{X>2Y}=∫02dx∫021x21dy=21 即 (U,V) 的联分布律为