引入
引例1:矩估计法通俗解释:某个调查小组要统计当地人员的平均工资,为此,他们随机的找了当地100个工作人员,算出这100个人的平均工资为5000元,由此他们推出,当地人平均工资5000元。可以看到在这里,我们直接使用样本的均值来当做总体的期望值。
引例2 :对某型号的 20 辆汽车记录其每 5 L 汽油的行驶里程 (单位: km ), 观测数据如下:
\begin{array}
29.8 & 27.6 & 28.3 & 27.9 & 30.1 & 28.7 & 29.9 & 28.0 & 27.9 & 28.7 \\
28.4 & 27.2 & 29.5 & 28.5 & 28.0 & 30.0 & 29.1 & 29.8 & 29.6 & 26.9
\end{array}
这是一个容量为 20 的样本观测值, 对应总体是该型号汽车每 5 L 汽油的行驶里程, 其分布形式尚不清楚, 可用矩法估计其均值、方差和中位数等. 本例中经计算有样本的均值方差和中位数
xˉ=28.695,s2=0.9668,m0.5=28.6, 由此给出总体均值、方差和中位数的估计分别为 28.695,0.9668 和 28.6.
上面两个例子虽然不同,但是处理方法类似,就是我们直接使用样本值来替代总体值,这种方法被称为矩估计法。因此矩法估计的统计思想十分简单明确,众人都能接受,使用场合甚广.
矩估计法的矩是k阶矩的意思。比如上面引例2中,我们用 样本期望拟合总体期望(相当于1阶原点矩),用 样本方差拟合总体方差(相当于2阶中心矩),如果继续使用样本的3阶矩、4阶矩拟合总体的3阶矩、4阶矩,会让样本越来越接近总体估算。关于k解决详见此处
基本概念
若总体 X 的分布已知,但它的一个或多个参数未知,则由总体 X 的样本去估计未知参数的值,此类问题就属于参数的点估计。
例如,设总体 X 的分布函数为 F(x;θ) ,其中 θ 为未知参数,由样本 X1,X2,⋯,Xn 构造一个统计量
θ^(X1,X2,⋯,Xn) 去估计未知参数 θ ,这种方法称为点估计,θ^(X1,X2,⋯,Xn) 称为参数 θ 的估计量.若 x1,x2,⋯,xn 是一组样本观测值,则 θ^(x1,x2,⋯,xn) 称为参数 θ 的估计值.
矩估计法
某工厂生产某种型号的钢筋,为了解此种钢筋的强度,我们从中抽取50根进行检查.如何从抽查的50根钢筋的强度数据去估计此种钢筋的平均强度µ呢?这就是参数估计要解决的问题.其中又分为两种情形:是找一个数值去估计µ,还是找一个范围去估计µ?
在上面估计钢筋强度的例子中,如果 50 根钢筋的强度数据已经检测完毕,我们可以用这 50 根钢筋的平均强度去估计此种钢筋的平均强度 μ ,即
μ^=xˉ=501i=1∑50xi 在实际问题中,我们常常以统计量
Xˉ=n1i=1∑nXi 作为总体X的期望值的估计量,这里用的就是矩估计法.
矩估计法的基本思想是替换原理,即用样本矩去替换相应的总体矩,这里的矩可以是原点矩,也可以是中心距.我们知道,矩是由随机变量的分布唯一确定的,而样本来源于总体,由大数定律可知,样本矩在一定程度上反映总体矩的特征
英国统计学家K.Pearson 皮尔逊于1900年提出了这个替换原理,后来人们称此方法为矩估计法或矩法(Moment Method of Estimation). 若估算的不够良好,再做适当调整.
矩估计的具体步骤
设总体 X 的分布函数 F(x;θ1,⋯,θk) 中含有 k 个未知参数 θ1,⋯,θk, 则:
(1) 设总体 X 的前 k 阶矩 μl=E(Xl)(1⩽l⩽k) 存在, 求出 μl=E(Xl)(1⩽l⩽k),一般都是这 k 个未知参数的函数, 记为
μl=μl(θ1,⋯,θk),l=1,2,⋯,k. (2) 设 Al(1⩽l⩽k) 为样本 k 阶矩, 用样本矩去替换总体矩, 即
令
⎩⎨⎧μ1(θ1,⋯,θk)=A1μ2(θ1,⋯,θk)=A2⋮μl(θ1,⋯,θk)=Al (3) 求出上面方程组的解 θ^1,θ^2,⋯,θ^k, 称 θ^l=θ^l(X1,X2,⋯,Xn) 为参数 θl(1⩽l⩽k)的矩估计量, θ^l=θ^l(x1,x2,⋯,xn) 为参数 θl(1⩽l⩽k) 的矩估计值.
在做矩估计时,既可用原点矩也可用中心矩建立关于未知参数的方程组,而且矩的阶数有多种选择,因而矩估计是不唯一的.为了计算方便,在矩估计中应该尽量采用低阶矩给出未知参数的矩估计.但通常估计使用期望和方差。
 {width=500px}
{width=500px}
例题
例 (离散型)设X为某零配件供应商每周的发货批次,其分布律如下.
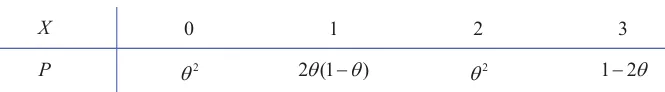 其中 θ 是未知参数.假设收集了该供应商 8 周的发货批次如下.
其中 θ 是未知参数.假设收集了该供应商 8 周的发货批次如下.
3,1,3,0,3,1,2,3. 求 θ 的矩估计值.
解 总体期望 E(X)=0×θ2+1×2θ(1−θ)+2×θ2+3×(1−2θ)=3−4θ .
样本均值 Xˉ=n1∑i=1nXi=81×(3+1+3+0+3+1+2+3)=2 .
用样本均值估计总体期望有 E(X)=Xˉ ,即 3−4θ=2 .
解得矩估计值为 θ^=41 .
例(连续型)已知某种金属板的厚度 X 在 (a,b) 上服从均匀分布,其中 a,b 未知.设抽查了 n 片金属板,厚度分别为 X1,X2,⋯,Xn 。试用矩估计法估计 a,b 。
解:我们在随机变量的数字特征上给出了均匀分布的期望和方差,即
X 若在 (a,b) 上服从均匀分布,
则
E(X)=2a+b,D(X)=12(b−a)2
总体的二阶矩
E(X2)=D(X)+E2(X)=12(b−a)2+(2a+b)2 ,
令
{E(X)=2a+b=XˉE(X2)=12(b−a)2+(2a+b)2=n1∑i=1nXi2 解此方程组,得到 a,b 的矩估计量分别为
(其中,B2=n1∑i=1n(Xi−Xˉ)2 为二阶样本中心距)
a^=Xˉ−n3i=1∑n(Xi−Xˉ)2=Xˉ−3B2b^=Xˉ+n3i=1∑n(Xi−Xˉ)2=Xˉ+3B2 点评 本题因为需要估计两个参数 a,b ,所以应该构造两个方程:(1)求出期望 EX 用 Xˉ 代替;
(2)求出 E(X2) 用 A2=n1∑i=1nXi2 代替,这样为
a^=Xˉ−3B2,b^=Xˉ+3B2
下面把上面抽象计算具体化,设厂钢板厚度服从均匀分布U(a,b),测量一批块钢板,其值为容量为 5 的样本:
4.55.04.74.04.2 经计算,有 xˉ=4.48,s=0.3962 ,于是可得 a,b 的矩估计为
a^=4.48−0.39623=3.7938,b^=4.48+0.39623=5.1662. 这样,我们就说,钢板服从 (3.794 ~ 5.166) 的均匀分布。
例 设总体 X 在 [a,b] 上服从均匀分布,(X1,X2,⋯,Xn) 为其样本,样本均值 Xˉ ,样本方差 S2 ,则 a,b 的矩估计 a^= ,b^= 。
解 由均匀分布的数字特征结论:
EX=2a+b,DX=12(b−a)2. 令 EX=Xˉ,DX=S2 ,解得
a^=Xˉ−3S,b^=Xˉ+3S 点评: 请仔细比较本例和上例的细微差别。因为a,b 是两个参数,所以需要2个方程。 上例使用期望和2解矩构造方程,本题使用期望和方差构造方程。所以,矩估计是不唯一的
例 设某种钛金属制品的技术指标为 X ,其概率密度为
f(x)={xβ+1β,0,x>1x⩽1 其中未知参数 β>1 .X1,X2,⋯,Xn 为来自总体 X 的简单随机样本,求 β 的矩估计量.
解 由于 E(X)=∫−∞+∞xf(x)dx=∫1+∞x⋅xβ+1βdx=β−1β ,令 β−1β=Xˉ ,解得 β=Xˉ−1Xˉ ,所以参数 β 的矩估计量为 β^=Xˉ−1Xˉ .
例设总体 X 服从正态分布 N(μ,σ2),(X1,X2,…,Xn) 是取自总体 X 的一个样本,
(1) 求 μ 的矩估计量;
(2) μ 已知, σ2 末知,求 σ2 的矩估计量;
(3) μ 和 σ2 都末知,求 σ2 的矩估计量.
解:(1)我们已经知道在正态分布里,其数学期望就是μ,而上面说过,矩估法里,总体的数学期望可用样本的数学期望代替,因此 μ=E(X) ,故 μ 的矩估计量 μ^=Xˉ ;
(2) σ2=D(X)=E(X2)−E2(X), 又因为 μ=E(X) 已知, 故 σ^2=n1∑i=1nXi2−μ2
(3) 因为 μ=E(X) 末知,故
σ^2=n1i=1∑nXi2−(Xˉ)2=n1i=1∑n(Xi−Xˉ)2=Sn2. 上面这个例子说明,正态分布里,总体的期望就是样本的期望,总体的方程就是样本的方差。
例设总体 X∼P(λ) ,其中 λ>0 未知, (X1,X2,⋯,Xn) 为取自该总体的一个样本.
试求:
(1)λ 的矩估计量;
(2)P(X=0) 的矩估计量.
解:(1) 因为 E(X)=λ ,故 λ 的矩估计量可定义为 λ^=Xˉ.
又 D(X)=λ=E(X2)−(EX)2 ,故 λ 的矩估计量又可写为 λ^=n1∑i=1nXi2−Xˉ2.
这说明矩估计可能不唯一,通常尽量采用较低阶的矩给出未知参数的估计。
(2) 因 P(X=0)=e−λ0!λ0=e−λ=e−E(X) 所以: P^(X=0)=e−Xˉ.
关于矩估计量有下列结论:
定理 设总体 X 的均值 E(X)=μ ,方差 D(X)=σ2,(X1,X2,⋯,Xn) 为取自该总体的一个样本,
则 Xˉ 是 μ 的矩估计量, Sn2 是 σ2 的矩估计量, Sn 是 σ 的矩估计量.
例设总体X的密度函数为
f(x,θ)={e−(x−θ)0,x≥θ 其它 ,其中θ 未知,(X1,X2,...Xn)未取自该总体的一个样本,求θ得矩估计量
解:因为 E(X)=∫θ+∞xe−(x−θ)dx=∫0+∞(t+θ)e−tdt=∫0+∞te−tdt+∫0+∞θe−tdt=1+θ
所以 θ=E(X)−1, 故 θ 的矩估计量 θ^=Xˉ−1.
例设 X∼U(−θ,θ),(X1,X2,⋯,Xn) 为取自该总体的 一个样本,求 θ(θ>0) 的矩估计量.
解 因 E(X)=0 ,而 E(X2)=D(X)=3θ2,
所以可由此解出 θ2=3E(X2),θ=3E(X2),
故 θ 的矩估计量为 θ^=3n1∑i=1nXi2.
例 设
X∼f(x,θ)={θ22x00<x<θ 其余 其中 θ>0 末知, 求 θ 的矩估计量.
解 由已知条件可求得
E(X)=∫−∞+∞xf(x)dx=∫0θxθ22x dx=32θ 故, θ=23E(X). 所以 θ^=23Xˉ.
 {width=500px}
{width=500px}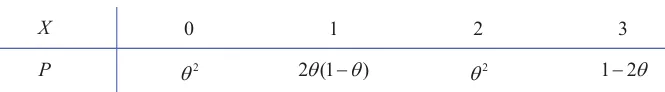 其中 是未知参数.假设收集了该供应商 8 周的发货批次如下.
其中 是未知参数.假设收集了该供应商 8 周的发货批次如下.