引言
引例1: 设有外形完全相同的两个箱子,甲箱中有 99 个白球和 1 个黑球,乙箱中有 99 个黑球和 1 个白球,今随机地抽取一箱,并从中随机抽取一球,结果取得白球,问这球是从哪一个箱子中取出?
解 不管是哪一个箱子,从箱子中任取一球都有两个可能的结果:A 表示"取出白球",B 表示"取出黑球"。如果我们取出的是甲箱,则 A 发生的概率为 0.99 ,而如果取出的是乙箱,则 A 发生的概率为 0.01 .现在一次试验中结果 A 发生了,人们的第一印象就是:"此白球 (A) 最像从甲箱取出的",或者说,应该认为试验条件对结果 A 出现有利,从而可以推断这球是从甲箱中取出的。这个推断很符合人们的经验事实,这里"最像"就是"最大似然"之意。这种想法常称为"最大似然原理"。
引例2: 我与一位猎人外出打猎,一只野鸡从前方飞过,只听一声枪响,野鸡应声落下.问:是谁打中的呢?
答:极有可能是猎人. 显然,候选人就两个,我和猎人.若选我,则事件“野鸡被打中”发生的概率很小,可能为0.01%,若选猎人,则事件“野鸡被打中”发生的概率很大,可能为99%,而事件已经发生,因此猎人最可能。
极大似然估计通俗理解
引入
例 设袋中放有很多的白球和黑球,已知两种球的比例为1∶9,但不知道哪种颜色的球多,现从中有放回地抽取3次,每次一球,发现前两次为黑球,第三次为白球,试判断哪种颜色的球多.
解:根据抽取结果,我们的直观感觉是黑球多,下面给出理论依据.
设 θ 表示黑球所占比例,由题意知 θ 的值为0.9或0.1,设X表示每次抽球中黑球出现的次数,则X服从(0−1)分布,其分布律如下
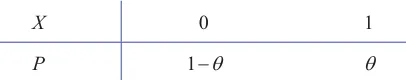
有放回地抽取 3 次,前两次为黑球,第三次为白球,相当于在总体 X 中抽取了一组样本 X1,X2,X3 ,样本观测值为 X1=1,X2=1,X3=0 ,判断哪种颜色的球多,相当于在事件 A={X1=1,X2=1,X3=0} 发生的前提下,判断 θ 的值是 0.9 还是 0.1.
P(A)=P{X1=1,X2=1,X3=0}=P{X1=1}P{X2=1}P{X3=0}=θ2(1−θ) 当 θ=0.9 时,P(A)=0.92×0.1=0.081 ;
当 θ=0.1 时,P(A)=0.12×0.9=0.009 .
根据最大似然估计法的基本原理,θ=0.9 应该有利于 A={X1=1,X2=1,X3=0} 的发生,即黑球多.
引申1
假设车间送来一盒螺丝,他们认为产品都是合格的,但是做为质检部门的我却不这么认为,我们总是默认里面有不合格的,但是不合格有多少我不知道(或者说不知道合格概率 p 为多少),我能做的只能抽查。
 {width=300px}
{width=300px}
现在我随机的有放回的从这盒螺丝抽取一个产品,然后记录他是否合格,一共抽查十次,假设随机变量为:
X= "抽查10次合格产品的次数" 那么该随机变量服从 p 未知的二项分布:
X∼b(10,p) 我们把螺丝抽查了10次,假设得到8个合格的,也就是得到了一个该二项分布的样本(此样本的容量为 1 ),要借此推断未知参数 p 为多少。首先列出得到8次合格的概率:
P(X=8)=C108p8(1−p)2...(1) ①假如说 p=0.7 ,那么上述概率为:
P(X=8)=C108∗0.78∗(1−0.7)2≈0.23 ②假如说 p=0.8 ,上述概率为:
P(X=8)=C108∗0.88∗(1−0.8)2≈0.30 ③假如说 p=0.9 ,那么上述概率为:
P(X=8)=C108∗0.98∗(1−0.9)2≈0.19 根据最大似然的思想,p=0.8 的可能性更大,所以应该认为 p=0.8 更接近于事实,即产品合格率在 80%
在上面计算过程中,可以看到所谓求最大似然的值,其实就是求函数(1)的最值(常数项可以忽略),设
L(p)=p8(1−p)2...(2) 方法1
只要对(2)求导并令导数为零即可,即
L′=2p7(1−p)(4−5p)=0...(3) 可得p=0,p=1,p=0.8 舍去不可能的值,所以p=0.8时,似然函数取得最大值。
方法2
对(2)两边取对数,这样会把右侧的乘法变成加法
LnL=8lnp+2ln(1−p)...(4) 再求导并令导数为零得
p8−1−p2=0 可以解的 p=0.8
假设车间说他们合格率为90%,但是我就可以利用数据来证明他们产品最大可能性为合格率为 80%
引申2
对于连续型的,以均匀分布为例,假设雨点均匀落在 [0,a] 之间,那么他的密度函数是 (注意:a未知,是我们要求的变量)
p(x)={a1,x∈a0,else 现在观察雨点实际落的位置是 0.1,0.4,0.4,0.3,0.6,怎么估算a的值?因为对连续性而言,每点的密度概率都是0的,为此,在这种情况下,我们使用联合概率密度函数计算他的最值,即
L(a)=an1 上面求L(a)的最大值,如果不可微,直接求是计算不了的,此时需要转换思维。
其实取 a为 max{x1,x2,..xn},具体参考下面视频解释。
下面视频介绍了取数的意义(视频来B站《小崔说数》)
<video width=600px height="500px"; controls>
极大似然估计定义
设总体有分布 f(X;θ1,⋯,θk),X1,⋯,Xn 为自这总体中抽出的样本, 则样本 (X1,⋯,Xn) 的分布 (即其概率密度函数或概率函数)为f(X1;θ1,⋯,θk)f(X2;θ1,⋯,θk)⋯f(Xn;θ1,⋯,θk)
记之为 L(X1,⋯,Xn;θ1,⋯,θk) 。
固定 θ1,⋯,θk 而看作是 X1,⋯,Xn 的函数时, L 是一个概率密度函数或概率函数,可以这样理解:
若 L(Y1,⋯,Yn;θ1,⋯,θk) >L(X1,⋯,Xn;θ1,⋯,θk), 则在观察时出现 (Y1,⋯,Yn) 这个点的可能性, 要比出现 (X1,⋯,Xn) 这个点的可能性大.
把这件事反过来说,可以这样想:当已观察到 X1,⋯,Xn 时,若 L(X1,⋯,Xn ; θ1′,⋯,θk′)>L(X1,⋯,Xn;θ1′′,⋯,θk′′) ,则被估计的参数 (θ1, ⋯,θk ) 是 (θ1′,⋯,θk′) 的可能性,要比它是 (θ1′′,⋯,θk′′) 的可能性大. (这里比较绕,可以参考上面引例理解)
当 X1,⋯,Xn 固定而把 L 看作 θ1,⋯,θk 的函数时, 它称为 "似然函数". 这名称的意义, 可根据上述分析得到理解: 这函数对不同的 (θ1,⋯,θk) 的取值,反映了在观察结果 (X1,⋯,Xn) 已知的条件下, (θ1,⋯,θk) 的各种值的"似然程度".
在 1821 年, 德国数学家高斯针对正态分布首先提出极(最)大似然估计(Maximum Likelihood Estimation, MLE)。英国统计学家费希尔于1922年再次提出了这种想法并证明了它的一些性质,使得最大似然估计法得到了广泛的应用。极大似然估计法只能在已知总体分布的前提下进行.
似然估计构造
构造步骤
上例的讨论可以推广到一般的离散型或连续型总体,具体步骤如下。
(1)构造似然函数
若总体 X 为离散型,其分布律为
P{X=xi}=p(xi;θ),θ∈Θ, 这里 θ 为待估参数,Θ 是 θ 可能取值的范围,对给定的样本观测值 x1,x2,⋯,xn ,令
L(θ)=L(x1,x2,⋯,xn;θ)=i=1∏np(xi;θ) 若总体 X 为连续型,其概率密度为
f(x;θ),θ∈Θ 这里 θ 为待估参数,Θ 是 θ 可能取值的范围,对给定的样本观测值 x1,x2,⋯,xn ,令
L(θ)=L(x1,x2,⋯,xn;θ)=i=1∏nf(xi;θ) L(θ) 随 θ 的取值而变化,它是 θ 的函数,我们称 L(θ) 为样本的似然函数.
似然函数实质上就是样本的联合分布,由上面的讨论可知,求待估参数的最大似然估计,实际上就是求似然函数的最大值点。
(2)求似然函数的最大值点
若有 θ^(x1,x2,⋯,xn) ,使
L(θ^)=θ∈Θmax{L(θ)} 则称 θ^=θ^(x1,x2,⋯,xn) 为参数 θ 的最大似然估计值,相应地,称 θ^=θ^(X1,X2,⋯,Xn) 为 θ 的最大似然估计量.
若似然函数可微,则似然函数的最大值点可以利用微积分方法求得,具体方法如下.
解似然方程
dθdL=0 得到参数 θ 的最大似然估计.
又因为 lnL(θ) 与 L(θ) 在同一点处取得极值,故可用对 lnL(θ) 求最大值的方法得到参数 θ 的最大似然估计,即先对似然函数 L(θ) 取对数,然后解对数似然方程
dθdlnL=0 当然,方程的解是否为最大值点,有时需进一步验证.
一般地,若总体 X 的分布中含有 k 个未知待估参数 θ1,θ2,⋯,θk ,则似然函数为
L(θ1,θ2,⋯,θk)=i=1∏nf(xi;θ1,θ2,⋯,θk) 此时只需要解似然方程组
∂θi∂L=0(i=1,2,⋯,k) 或对数似然方程组
∂θi∂lnL=0(i=1,2,⋯,k) 即可得到参数的最大似然估计 θ^1,θ^2,⋯,θ^k .
例设 X∼b(1,p),X1,X2,⋯,Xn 是取自总体 X 的一个样本,试求参数 p 的最大似然估计。
解(1)写出似然函数.
设 x1,x2,⋯,xn 是 X1,X2,⋯,Xn 的一个样本值,X 的分布律为
P{X=x}=px(1−p)1−x,x=0,1 故似然函数为
L(p)=i=1∏npxi(1−p)1−xi=p∑i=1nxi(1−p)n−∑i=1nxi (2)求出驻点.
令
dpdlnL(p)=(i=1∑nxi)/p−(n−i=1∑nxi)/(1−p)=0 解得
p^=n1i=1∑nxi=xˉ (3)即参数 p 的最大似然估计为
p^=n1i=1∑nXi=Xˉ 注意:这一估计量与矩估计量是相同的.
似然函数取对数
当 θ=(θ1,θ2,⋯,θk) 的似然函数
L(θ)=L(θ1,θ2,⋯,θk) 从似然函数可以看出,他是L=f(1)∗f(2)∗f(3)...f(n) 这种连乘的形式,这计算起来非常麻烦,所以可以取对出,利用对数的性质把乘法变成加法,即
lnL=ln(f(1)∗f(2)∗f(3)...f(n))=ln(f(1))+ln(f(2))...+lnf(n)
因此,当可微函数时,则将似然函数取对数:
lnL(θ1,θ2,⋯,θk)=i=1∑nlnf(xi,θ1,θ2,⋯,θk) 建立并求解似然方程组:
∂θi∂lnL(θ1,θ2,⋯,θk)=0,i=1,2,⋯,k 例设总体 X 的密度函数为 f(x)={λ2xe−λx,x>00, 其他 ,其中 λ(λ>0) 未知, (X1,…,Xn) 是来自总体 X 的一个样本.求 λ 的极大似然估计量.
解 似然函数
L(λ)=i=1∏nf(xi;λ)=λ2n⋅i=1∏nxi⋅e−λ∑i=1nxi 取对数似然函数为
lnL=2nlnλ+i=1∑nlnxi−λi=1∑nxi 对数似然方程为
dλdlnL=λ2n−i=1∑nxi=0 解得
λ=∑i=1nxi2n=n1∑i=1nxi2 故 λ 的极大似然估计量为 λ^=Xˉ2.
例 设某种元件的使用寿命 X 的概率密度为
f(x)={2e−2(x−θ),0,x⩾θ, 其他, 其中 θ>0 ,且 θ 是末知参数.设 x1,x2,⋯,xn 是样本观测值,求 θ 的最大似然估计值.
解 似然函数为
L(θ)=i=1∏nf(xi)=i=1∏n[2e−2(xi−θ)]=2ne−2∑i=1n(xi−θ),xi⩾θ, 取对数得
lnL(θ)=nln2−2i=1∑n(xi−θ) 因为 dθdlnL(θ)=2n>0 ,所以 L(θ) 单调增加.而
θ⩽xi(i=1,2,⋯,n) 故 θ 的最大似然估计值为
θ^=min{x1,x2,⋯,xn} 例 设某工厂生产的手机屏幕分为不同的等级,其中一级品率为 p ,如果从生产线上抽取了 20 件产品,发现其中有 3 件为一级品,求:
(1)p 的最大似然估计值;
(2)接着再抽取 5 件产品都不是一级品的概率的最大似然估计值.
解(1)因为每件产品有两种可能,即要么是一级品,要么不是一级品,所以总体 X 服从 (0-1)分布,其分布律为
p(x)=P{X=x}=px(1−p)1−x,x=0,1. 20 件产品中有 3 件为一级品,相当于样本观测值 x1,x2,⋯,x20 中有 3 个为 1 ,有 17 个为 0 ,故似然函数为
L(p)=i=1∏np(xi)=p3(1−p)17. 取对数得
lnL(p)=3lnp+17ln(1−p) 对 p 求导得
dpdlnL(p)=p3−1−p17 令
dpdlnL(p)=0 可得 p=203 .故 p 的最大似然估计值为 p^=203 .
(2)因为一级品率为 p ,所以再抽取 5 件产品都不是一级品的概率为 (1−p)5 .
既然 20 件产品中有 3 件为一级品,此时得到的 p 的最大似然估计值为 p^=203 ,那么
(1−p)5 的最大似然估计值为 (1−p^)5=(1−203)5=0.4437 .
注意,这里我们用到了"最大似然估计不变性",即以下定理.
最大似然估计不变性
定理 若 θ^ 为参数 θ 的最大似然估计,g(θ) 为参数 θ 的函数,则 g(θ^) 是 g(θ) 的最大似然估计。
有了最大似然估计不变性,求某些复杂结构的参数的最大似然估计就变得容易了.
例设总体 X∼N(μ,σ2),(X1,⋯,Xn) 是取自该总体的一个样本,参数 μ∈R,σ>0 未知试求(1) μ,σ2 的极大似然估计量;(2) θ≐P(X≥2) 的极大似然估计量。
解 (1)①写出似然函数
L(μ,σ2)=(2πσ2)−2ne−2σ21∑i=1n(xi−μ)2−∞<xi<+∞,i=1,2,⋯,n ②对似然函数取对数:
lnL(μ,σ2)=−2nln2π−2nlnσ2−2σ21i=1∑n(xi−μ)2 ③建立似然方程组:
{∂μ∂lnL=σ21∑i=1n(xi−μ)=^0∂σ2∂lnL=−2σ2n+2σ41∑i=1n(xi−μ)2=0^ 解方程组得
{μ=n1∑i=1nxi=xˉσ2=n1∑i=1n(xi−μ)2=n1∑i=1n(xi−xˉ)2 ④由此即得未知参数的极大似然估计量为
μ^=Xˉ,σ^2=n1i=1∑n(Xi−Xˉ)2=Sn2 (2)已经求得 μ^=Xˉ,σ^=Sn, 又
θ=^P(X≥2)=1−Φ(σ2−μ) 以 μ^,σ^ 替代 μ,σ 即得 θ 的极大似然估计量为
θ^=1−Φ(σ^2−μ^)=1−Φ(Sn2−Xˉ) 第(2)问的解题过程用到了极大似然估计的不变性:如果 θ^ 是 θ 的极大似然估计,则对任一函数 g(θ) ,满足当 θ∈Θ 时,具有单值反函数,则其极大似然估计为 g(θ^) 。
解法总结
如果随机抽样得到的样本观测值为 x1,x2,⋯,xn, 我们选取未知参数 θ 的值应使得出现该样本值的可能性最大,即使得似然函数 L(θ) 取最大值,从而,求参数 θ 的极大似然估计的问题就转化为求似然函数 L(θ) 的最大值点的问题,当似然函数关于未知参数可微时,可利用微分学中求最大值的方法求解. 其主要步骤如下:
(1)写出似然函数 L(θ)=L(θ;x1,x2,⋯,xn);
(2)令 dθdL(θ)=0 或 dθdlnL(θ)=0 ,求出驻点;
(3)判断并求出最大值点,在最大值点的表达式中,用样本值代入就得参数的最大似然估计值。
注意:(1)因函数 lnL(θ) 是 L(θ) 的单调增加函数,且函数 lnL(θ) 与函数 L(θ) 有相同的极值点,故转化为求函数 lnL(θ) 的最大值点较方便。
(2)当似然函数关于未知参数不可微时,只能按最大似然估计法的基本思想及定义求出最大值点。
(3)从最大似然估计的定义可以看出,若 L(θ) 与联合概率函数相差一个与 θ 无关的比例因子, 则不会影响最大似然估计, 可以在 L(θ) 中剔去与 θ 无关的因子。
例 设总体 X 服从 [0,θ] 上的均匀分布, θ 末知. X1,⋯,Xn 为 X 的样本, x1,⋯,xn为样本值. 试求 θ 的最大似然估计.
解 似然函数 L(θ)={θn1,0,0⩽x1,⋯,xn⩽θ 其他 .
因 L(θ) 不可导, 可按最大似然法的基本思想确定 θ^ 。欲使 L(θ) 最大, θ 应尽量小但又不能太小, 它必须同时满足 θ⩾xi(i=1,⋯,n), 即 θ⩾max(x1,⋯,xn), 否则 L(θ)=0, 而 0 不可能是 L(θ) 的最大值. 因此, 当 θ=max{x1,⋯,xn} 时, L(θ) 可达最大. 所以 θ 的最大似然估计为 θ^=max{X1,⋯,Xn}.
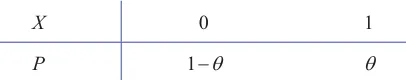
 {width=300px}
{width=300px}