单侧检验
前面我们讨论的参数检验,拒绝域取在两侧,一般称为双侧检验.但是在实际问题中,有时关心的不是参数是否等于某个值,而是参数是否大于或小于某个值,例如:采取新工艺后,纺织物的强力指标是否有提高?经过政策调控,本月猪肉的均价是否有所下降?等等。此时根据检验假设,拒绝域应该取在某一侧,称为单侧检验.下面以正态总体关于 μ 的检验为例来说明.
设总体 X∼N(μ,σ2),X1,X2,⋯,Xn 是取自总体 X 的一个样本,给定显著性水平为 α(0<α< 1) ,若 σ2 已知,检验 μ 是否增大?
首先建立假设
H0:μ=μ0,H1:μ>μ0 或
H0:μ⩽μ0,H1:μ>μ0 选取检验统计量
U=nσXˉ−μ0∼N(0,1). 当 H0 为真时,U=nσXˉ−μ0 不应太大,则 U 偏大时应拒绝 H0 ,故按照显著性水平 α ,如图 7.2 所示,构造小概率事件为
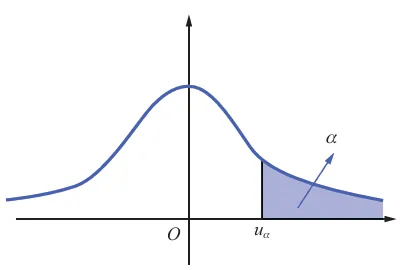
P{U>uα}=α, 即拒绝域 U>uα .
由样本观测值求出 U 的观测值 u ,然后做判断.
例 某地区的物价部门对当前市场的大米价格情况进行调查,共调查了 30 个集市上的大米售价,测得它们的平均价格为 2.21 元 /500g ,已知以往大米的平均售价一直稳定在 2 元/ 500 g 。如果该地区大米的售价服从正态分布 N(μ,0.18) ,假定方差不变,能否根据上述数据认为该地区当前的大米售价明显高于往年?(α=0.05)
(解)根据题意知,需检验假设 H0:μ⩽2,H1:μ>2 。
检验统计量为
U=σ/nXˉ−2∼N(0,1) 当 α=0.05 时,拒绝域 U>uα 为 U>u0.05 ,也即 U>1.65 。
将 xˉ=2.21,σ2=0.18,n=30 代入检验统计量中可得
u=2.7>1.65, 故应拒绝 H0 ,即认为该地区当前的大米售价明显高于往年.
例 现有甲、乙两台车床加工同一型号的螺钉,根据以往经验认为两台车床加工的螺钉长度都服从正态分布.现从这两台车床加工的螺钉中分别抽取 11 个和 9 个,测得长度(单位:mm)分别如下.
甲: 6.2,5.7,6.0,6.3,6.5,6.0,5.7,5.8,6.0,5.8,6.0 .
乙:5.6,5.7,5.9,5.5,5.6,6.0,5.8,5.5,5.7.
问:乙车床的加工精度是否高于甲车床(即乙车床加工的螺钉长度的方差是否比甲车床的小)?( α=0.05 )
解 设 X 和 Y 分别表示甲、乙两台车床加工的螺钉的长度,则
X∼N(μ1,σ12),Y∼N(μ2,σ22). 依题意知,需检验假设 H0:σ12⩽σ22,H1:σ12>σ22 。
检验统计量为
F=S22S12∼F(n1−1,n2−1) 拒绝域为 F>Fα(n1−1,n2−1) .
这里 n1=11,n2=9,α=0.05 ,从而 Fα(n1−1,n2−1)=F0.05(10,8)=3.35 .
由样本值算得 s12=0.064,s22=0.030 ,于是
f=s22s12=0.0300.064=2.13<3.35 故接受 H0 ,即不能认为乙车床的加工精度高于甲车床.
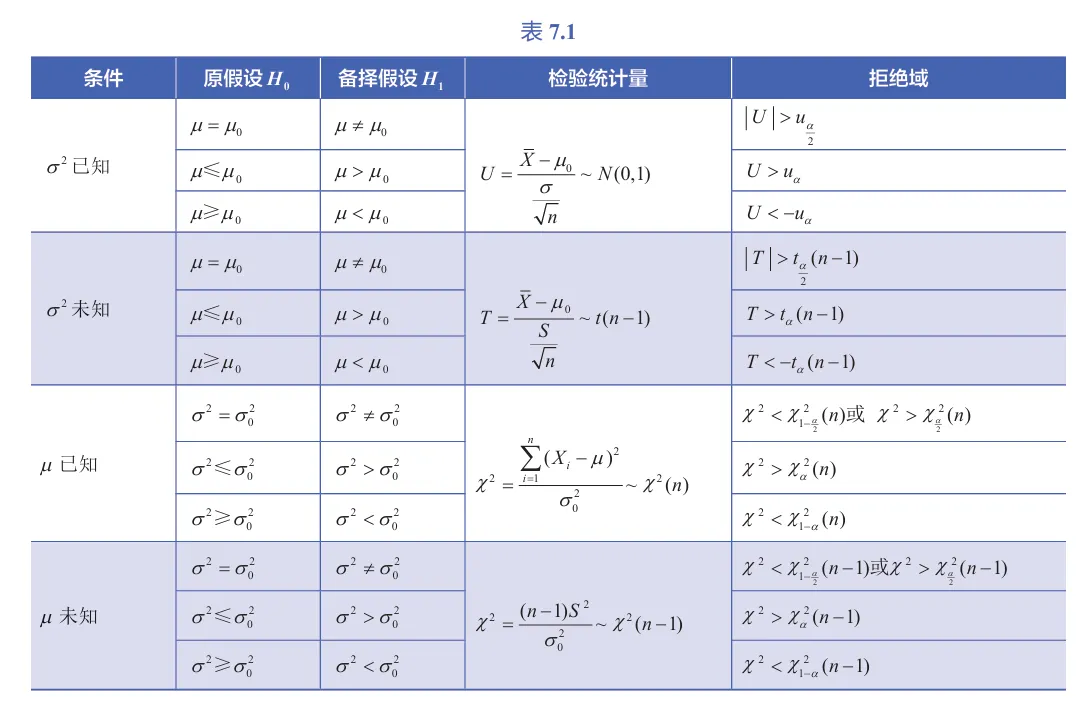
对以上关于正态总体参数的假设检验的讨论进行总结,单个正态总体参数的假设检验如表 7.1 所示,两个正态总体参数的假设检验附表.