总体分布的卡方检验法 前面讨论的参数检验问题是在总体分布类型已知的情况下,对其中的未知参数进行检验。在实际问题中,有时并不知道总体的具体分布情况,这时就需要从总体中抽取的样本对总体的分布进行推断,以判断总体服从何种分布,这类统计检验称为非参数检验。例如检验假设"总体服从正态分布"等。本节仅介绍 χ 2 \chi^2 χ 2 χ 2 \chi^2 χ 2 χ 2 \chi^2 χ 2 X X X X 1 , X 2 , ⋯ , X n X_1, X_2, \cdots, X_n X 1 , X 2 , ⋯ , X n F ( x ) F(x) F ( x ) F 0 ( x ) F_0(x) F 0 ( x )
H 0 : F ( x ) = F 0 ( x ) , H_0: F(x)=F_0(x), H 0 : F ( x ) = F 0 ( x ) , 该分布的检验问题是根据样本的观察值 x 1 , x 2 , ⋯ , x n x_1, x_2, \cdots, x_n x 1 , x 2 , ⋯ , x n χ 2 \chi^2 χ 2
总体 X X X 设总体 X X X b 1 , b 2 , ⋯ b_1, b_2, \cdots b 1 , b 2 , ⋯ b i b_i b i x 1 , x 2 , ⋯ , x n x_1, x_2, \cdots, x_n x 1 , x 2 , ⋯ , x n B 1 , B 2 , ⋯ , B k B_1, B_2, \cdots, B_k B 1 , B 2 , ⋯ , B k b 1 , b 2 , ⋯ b_1, b_2, \cdots b 1 , b 2 , ⋯ k k k n i n_i n i B i B_i B i
P ( X ∈ B i ) = p i ( i = 1 , 2 , ⋯ , k ) , P\left(X \in B_i\right)=p_i \quad(i=1,2, \cdots, k), P ( X ∈ B i ) = p i ( i = 1 , 2 , ⋯ , k ) , 则假设
H 0 : F ( x ) = F 0 ( x ) H_0: F(x)=F_0(x) H 0 : F ( x ) = F 0 ( x ) 可以转化为如下假设
H 0 : B i 所占的比例为 p i ( i = 1 , 2 , ⋯ , k ) , H_0: B_i \text { 所占的比例为 } p_i \quad(i=1,2, \cdots, k) \text {, } H 0 : B i 所占的比例为 p i ( i = 1 , 2 , ⋯ , k ) , 即
H 0 : P ( B i ) = p i ( i = 1 , 2 , ⋯ , k ) H_0: \quad P\left(B_i\right)=p_i \quad(i=1,2, \cdots, k) H 0 : P ( B i ) = p i ( i = 1 , 2 , ⋯ , k ) 现对总体做了 n n n n 1 , n 2 , ⋯ , n k n_1, n_2, \cdots, n_k n 1 , n 2 , ⋯ , n k
∑ i = 1 k n i = n \sum_{i=1}^k n_i=n i = 1 ∑ k n i = n 当 H 0 H_0 H 0 p i p_i p i n i n \frac{n_i}{n} n n i n i n_i n i n p i n p_i n p i n i − n p i n_i-n p_i n i − n p i
χ 2 = ∑ i = 1 k ( n i − n p i ) 2 n p i . \chi^2=\sum_{i=1}^k \frac{\left(n_i-n p_i\right)^2}{n p_i} . χ 2 = i = 1 ∑ k n p i ( n i − n p i ) 2 . 其中取偏差平方是为了把偏差积累起来,每项除以 n p i n p_i n p i n p i n p_i n p i ( n i − n p i ) 2 \left(n_i-n p_i\right)^2 ( n i − n p i ) 2
定理 当 n n n ( n ⩾ 50 ) (n \geqslant 50) ( n ⩾ 50 ) χ 2 = ∑ i = 1 k ( n − n p i ) 2 n p i \chi^2=\sum_{i=1}^k \frac{\left(n-n p_i\right)^2}{n p_i} χ 2 = ∑ i = 1 k n p i ( n − n p i ) 2 χ 2 ( k − 1 ) \chi^2(k-1) χ 2 ( k − 1 ) α \alpha α l l l
P { χ 2 > l } = α P\left\{\chi^2>l\right\}=\alpha P { χ 2 > l } = α 求得 l = χ α 2 ( k − 1 ) l=\chi_\alpha^2(k-1) l = χ α 2 ( k − 1 )
χ 2 > χ α 2 ( k − 1 ) \chi^2>\chi_\alpha^2(k-1) χ 2 > χ α 2 ( k − 1 ) 若由所给的样本值 x 1 , x 2 , ⋯ , x n x_1, x_2, \cdots, x_n x 1 , x 2 , ⋯ , x n χ 2 \chi^2 χ 2 H 0 H_0 H 0 H 0 H_0 H 0
例 将一颗骰子郑 120 次,所得数据为
问这颗骰子是否均匀,对称(取 α = 0.05 \alpha=0.05 α = 0.05 1 ∼ 6 1 \sim 6 1 ∼ 6 1 / 6 1 / 6 1/6 A i A_i A i i i i ( i = 1 , 2 , ⋯ , 6 ) (i=1,2, \cdots, 6) ( i = 1 , 2 , ⋯ , 6 ) H 0 : P ( A i ) = 1 / 6 , i = 1 , 2 ⋯ , 6 H_0: P\left(A_i\right)=1 / 6, i=1,2 \cdots, 6 H 0 : P ( A i ) = 1/6 , i = 1 , 2 ⋯ , 6
在 H 0 H_0 H 0 p i = p ( A i ) = 1 / 6 p_i=p\left(A_i\right)=1 / 6 p i = p ( A i ) = 1/6 n = 120 n=120 n = 120 n p i = 20 n p_i=20 n p i = 20
因此分布不含未知参数,又 k = 6 , α = 0.05 k=6, \alpha=0.05 k = 6 , α = 0.05 χ α 2 ( k − 1 ) = χ 0.05 2 ( 5 ) = 11.071 \chi_\alpha^2(k-1)=\chi_{0.05}^2(5)=11.071 χ α 2 ( k − 1 ) = χ 0.05 2 ( 5 ) = 11.071 χ 2 = ∑ i = 1 6 ( n i − n p i ) 2 n p i = 4.8 < 11.071 \chi^2=\sum_{i=1}^6 \frac{\left(n_i-n p_i\right)^2}{n p_i}=4.8<11.071 χ 2 = ∑ i = 1 6 n p i ( n i − n p i ) 2 = 4.8 < 11.071 H 0 H_0 H 0
总体 X X X 设 X 1 , X 2 , ⋯ , X n X_1, X_2, \cdots, X_n X 1 , X 2 , ⋯ , X n X X X x 1 , x 2 , ⋯ , x n x_1, x_2, \cdots, x_n x 1 , x 2 , ⋯ , x n F 0 ( x ) F_0(x) F 0 ( x )
H 0 : X 服从连续分布 F 0 ( x ) H_0: X \text { 服从连续分布 } F_0(x) H 0 : X 服从连续分布 F 0 ( x ) 这类问题称为连续分布的拟合优度检验问题。具体步骤如下.
(1)把 X X X k k k A 1 , A 2 , ⋯ , A k A_1, A_2, \cdots, A_k A 1 , A 2 , ⋯ , A k
( a 0 , a 1 ] , ( a 1 , a 2 ] , ⋯ , ( a k − 2 , a k − 1 ] , ( a k − 1 , a k ) \left(a_0, a_1\right],\left(a_1, a_2\right], \cdots,\left(a_{k-2}, a_{k-1}\right],\left(a_{k-1}, a_k\right) ( a 0 , a 1 ] , ( a 1 , a 2 ] , ⋯ , ( a k − 2 , a k − 1 ] , ( a k − 1 , a k ) 其中 a 0 < a 1 < ⋯ < a k − 1 < a k , a 0 a_0<a_1<\cdots<a_{k-1}<a_k, a_0 a 0 < a 1 < ⋯ < a k − 1 < a k , a 0 − ∞ , a k -\infty, a_k − ∞ , a k + ∞ +\infty + ∞ k k k i i i A i A_i A i k k k k k k H 0 H_0 H 0 X X X i i i A i A_i A i
p i = P ( a i − 1 < X < a i ) = F 0 ( a i ) − F 0 ( a i − 1 ) , i = 1 , 2 , ⋯ , k p_i=P\left(a_{i-1}<X<a_i\right)=F_0\left(a_i\right)-F_0\left(a_{i-1}\right), \quad i=1,2, \cdots, k p i = P ( a i − 1 < X < a i ) = F 0 ( a i ) − F 0 ( a i − 1 ) , i = 1 , 2 , ⋯ , k 样本观测值落入这 k k k n 1 , n 2 , ⋯ , n k n_1, n_2, \cdots, n_k n 1 , n 2 , ⋯ , n k X X X
F ( x , θ 1 , θ 2 , ⋯ , θ r ) , F\left(x, \theta_1, \theta_2, \cdots, \theta_r\right), F ( x , θ 1 , θ 2 , ⋯ , θ r ) , 其中 θ 1 , θ 2 , ⋯ , θ r \theta_1, \theta_2, \cdots, \theta_r θ 1 , θ 2 , ⋯ , θ r X 1 , X 2 , ⋯ , X n X_1, X_2, \cdots, X_n X 1 , X 2 , ⋯ , X n X X X
H 0 : 总体 X 的分布函数为 F ( x , θ 1 , θ 2 , ⋯ , θ r ) , H_0 \text { : 总体 } X \text { 的分布函数为 } F\left(x, \theta_1, \theta_2, \cdots, \theta_r\right) \text {, } H 0 : 总体 X 的分布函数为 F ( x , θ 1 , θ 2 , ⋯ , θ r ) , 此类情况可按如下步骤进行检验:
(1)利用样本 X 1 , X 2 , ⋯ , X n X_1, X_2, \cdots, X_n X 1 , X 2 , ⋯ , X n θ 1 , θ 2 , ⋯ , θ r \theta_1, \theta_2, \cdots, \theta_r θ 1 , θ 2 , ⋯ , θ r θ ^ 1 , θ ^ 2 , ⋯ , θ ^ r \hat{\theta}_1, \hat{\theta}_2, \cdots, \hat{\theta}_r θ ^ 1 , θ ^ 2 , ⋯ , θ ^ r θ ^ i \hat{\theta}_i θ ^ i F ( x , θ 1 , θ 2 , ⋯ , θ r ) F\left(x, \theta_1, \theta_2, \cdots, \theta_r\right) F ( x , θ 1 , θ 2 , ⋯ , θ r ) θ i ( i = 1 , 2 , ⋯ , r ) \theta_i(i=1,2, \cdots, r) θ i ( i = 1 , 2 , ⋯ , r ) F ( x , θ ^ 1 , θ ^ 2 , ⋯ , θ ^ r ) F\left(x, \hat{\theta}_1, \hat{\theta}_2, \cdots, \hat{\theta}_r\right) F ( x , θ ^ 1 , θ ^ 2 , ⋯ , θ ^ r ) p i p_i p i p ^ i ( i = 1 , 2 , ⋯ , k ) \hat{p}_i(i=1,2, \cdots, k) p ^ i ( i = 1 , 2 , ⋯ , k )
χ 2 = ∑ i = 1 k ( n i − n p ^ i ) 2 / n p ^ i \chi^2=\sum_{i=1}^k\left(n_i-n \hat{p}_i\right)^2 / n \hat{p}_i χ 2 = i = 1 ∑ k ( n i − n p ^ i ) 2 / n p ^ i 当 n n n χ 2 \chi^2 χ 2 χ α 2 ( k − r − 1 ) \chi_\alpha^2(k-r-1) χ α 2 ( k − r − 1 ) k k k r r r α \alpha α
χ 2 = ∑ i = 1 k ( n i − n p ^ i ) 2 / n p ^ i > χ α 2 ( k − r − 1 ) . \chi^2=\sum_{i=1}^k\left(n_i-n \hat{p}_i\right)^2 / n \hat{p}_i>\chi_\alpha^2(k-r-1) . χ 2 = i = 1 ∑ k ( n i − n p ^ i ) 2 / n p ^ i > χ α 2 ( k − r − 1 ) . 注意:在使用皮尔逊 χ 2 \chi^2 χ 2 n ⩾ 50 n \geqslant 50 n ⩾ 50 n p i ⩾ 5 ( i = 1 , ⋯ , k ) n p_i \geqslant 5(i=1, \cdots, k) n p i ⩾ 5 ( i = 1 , ⋯ , k ) n p i n p_i n p i
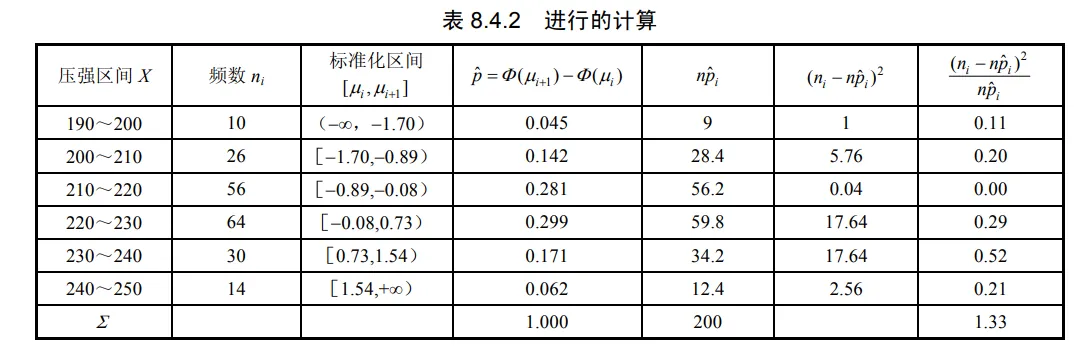
例研究混凝土抗压强度的分布. 200 件混凝土制件的抗压强度以分组形式列出(如表 8.4.1 所示).n = ∑ i = 1 6 n i = 200 n=\sum_{i=1}^6 n_i=200 n = ∑ i = 1 6 n i = 200 α = 0.05 \alpha=0.05 α = 0.05
H 0 : 抗压强度 X ∼ N ( μ , σ 2 ) . H_0: \text { 抗压强度 } X \sim N\left(\mu, \sigma^2\right) \text {. } H 0 : 抗压强度 X ∼ N ( μ , σ 2 ) . 表 8.4.1 200 件混凝土制件的抗压强度
μ \mu μ σ 2 \sigma^2 σ 2 μ \mu μ σ 2 \sigma^2 σ 2
μ ^ = x ˉ σ ^ 2 = ∑ i = 1 n ( x i − x ˉ ) 2 / n \begin{gathered}
\hat{\mu}=\bar{x} \\
\hat{\sigma}^2=\sum_{i=1}^n\left(x_i-\bar{x}\right)^2 / n
\end{gathered} μ ^ = x ˉ σ ^ 2 = i = 1 ∑ n ( x i − x ˉ ) 2 / n 设 x i ∗ x_i^* x i ∗ i i i
x ˉ = 1 n ∑ i = 1 6 x i ∗ n i = 195 × 10 + 205 × 26 + ⋯ + 245 × 14 200 = 221 , σ ^ 2 = 1 n ∑ i = 1 n ( x i ∗ − x ˉ ) 2 n i = 1 200 { ( − 26 ) 2 × 10 + ( − 16 ) 2 × 26 + ⋯ + 24 2 × 14 } = 152 , σ ^ = 12.33. \begin{gathered}
\bar{x}=\frac{1}{n} \sum_{i=1}^6 x_i^* n_i=\frac{195 \times 10+205 \times 26+\cdots+245 \times 14}{200}=221, \\
\hat{\sigma}^2=\frac{1}{n} \sum_{i=1}^n\left(x_i^*-\bar{x}\right)^2 n_i=\frac{1}{200}\left\{(-26)^2 \times 10+(-16)^2 \times 26+\cdots+24^2 \times 14\right\}=152, \\
\hat{\sigma}=12.33 .
\end{gathered} x ˉ = n 1 i = 1 ∑ 6 x i ∗ n i = 200 195 × 10 + 205 × 26 + ⋯ + 245 × 14 = 221 , σ ^ 2 = n 1 i = 1 ∑ n ( x i ∗ − x ˉ ) 2 n i = 200 1 { ( − 26 ) 2 × 10 + ( − 16 ) 2 × 26 + ⋯ + 2 4 2 × 14 } = 152 , σ ^ = 12.33. 原假设 H 0 H_0 H 0 X X X N ( 221 , 12.33 2 ) N\left(221,12.33^2\right) N ( 221 , 12.3 3 2 )
p ^ i = P ( a i − 1 < X < a i ) = Φ ( μ i ) − Φ ( μ i − 1 ) , i = 1 , 2 , ⋯ , 6 \hat{p}_i=P\left(a_{i-1}<X<a_i\right)=\Phi\left(\mu_i\right)-\Phi\left(\mu_{i-1}\right), \quad i=1,2, \cdots, 6 p ^ i = P ( a i − 1 < X < a i ) = Φ ( μ i ) − Φ ( μ i − 1 ) , i = 1 , 2 , ⋯ , 6 其中
μ i = a i − x ˉ σ ^ \mu_i=\frac{a_i-\bar{x}}{\hat{\sigma}} μ i = σ ^ a i − x ˉ Φ ( μ i ) = 1 2 π ∫ − ∞ μ i e − t 2 2 d t \Phi\left(\mu_i\right)=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\mu_i} e^{-\frac{t^2}{2}} d t Φ ( μ i ) = 2 π 1 ∫ − ∞ μ i e − 2 t 2 d t 为了计算统计量 χ 2 \chi^2 χ 2
从上面计算得出 χ 2 \chi^2 χ 2 a = 0.05 a=0.05 a = 0.05 m = 6 − 2 − 1 = 3 m=6-2-1=3 m = 6 − 2 − 1 = 3 χ 2 \chi^2 χ 2 χ 0.05 2 ( 3 ) = 7.815 \chi_{0.05}^2(3)=7.815 χ 0.05 2 ( 3 ) = 7.815 χ 2 = 1.33 < 7.815 = χ 0.05 2 ( 3 ) \chi^2=1.33<7.815=\chi_{0.05}^2(3) χ 2 = 1.33 < 7.815 = χ 0.05 2 ( 3 ) N ( 221 , 152 ) N(221,152) N ( 221 , 152 )
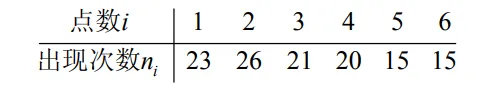


 解 原假设所定的正态分布的参数是未知的,需先求 和 的极大似然估计值.由第 7章知, 和 的极大似然估计值为
解 原假设所定的正态分布的参数是未知的,需先求 和 的极大似然估计值.由第 7章知, 和 的极大似然估计值为