拟合优度检验
第七章的参数估计是假定总体的分布类型是已知的,需要通过样本来估计刻画总体分布的一个或若干个参数。但是,在实际问题中,经常不知道总体服从什么分布,这时只能假定其为某种分布,那么就需要根据样本数据来检验假设是否合理,即检验假设的总体分布是否可以被接受, 又称为分布的拟合检验, 常用的方法有 χ2 拟合优度检验.
例 检验一枚骰子是否是均匀的ꎬ 首先抛掷一枚骰子 120 次 得到如下结果记录

在显著性水平 α=0.01 水平下, 请问, 这枚股子是否是均匀的?
分析 设 X 为骰子出现的点数,根据题意可以假设 X 的分布为
H0:P(X=i)=pi=61,i=1,2,⋯,6. 如果骰子是均匀的,即在 H0 成立的假定下,投掷 120 次,平均来说每个点面应该都出现 npi=120⋅61=20 次, 这称为理论频数, 如果每个点面实际出现次数与 20 次相差不大, 那么可以说明股子是均匀的, 如果相差太大, 例如有些点面严重偏多, 而另外一些点面严重偏少,那么可以说明股子是不均匀的。由于有正偏差就一定有负偏差,所以用偏差平方的方式来计算每一个点面出现的偏差, 并计算所有点面累积的总偏差, 如果总偏差太大,超过了容忍的最大值 c ,就拒绝原假设,即认为骰子是不均匀的,反之,则不拒绝骰子是均匀的原假设.
根据上述分析,我们构造拒绝域的形式为 W={∑i=1k(Ni−npi)2>c} ,其中 Ni 表示第 i 个点面实际出现的次数,又称为实际频数;当我们有了一组样本观测值以后, Ni 的观测值记为 ni. 其中的 k 表示总体分布取值分组的组数,例如在例 1 中, k 取 6 。
那么这里的容忍最大值 c 取何值呢?
根据显著性水平的定义,容忍最大值 c 需满足
P((X1,X2,⋯,Xn)∈W)=P(i=1∑k(Ni−npi)2>c∣H0 成立 )⩽α. 统计学家 K - 皮尔逊基于上述拒绝域的形式构造了一个检验统计量
χ2=i=1∑knpi(Ni−npi)2 并证明了如下重要的结论, 我们以定理的方式不加证明地给出.
定理1 如果原假设 H0:P(X=i)=pi,i=1,2,⋯,k 成立, 则当样本量 n→∞ 时, χ2=∑i=1knpi(Ni−npi)2 的极限分布是自由度为 k−1 的 χ2 分布,即
χ2=i=1∑knpi(Ni−npi)2∼χ2(k−1), 所以
P((X1,X2,⋯,Xn)∈W)=P(i=1∑knpi(Ni−npi)2>X1−α2(k−1)H0 成立 )⩽α. 即拒绝域为
W={i=1∑knpi(Ni−npi)2>χ1−α2(k−1)}. 在例 1 中, χ2 检验统计量的观测值,
χ2=i=1∑knpi(ni−npi)2=20(23−20)2+20(26−20)2+20(21−20)2+20(20−20)2+20(15−20)2+20(15−20)2=4.8. 查表 可得, χ0.992(5)=15.0863>4.8, 所以, 在显著性水平 α=0.01 下接受原假设,即可认为这枚骰子是均匀的。
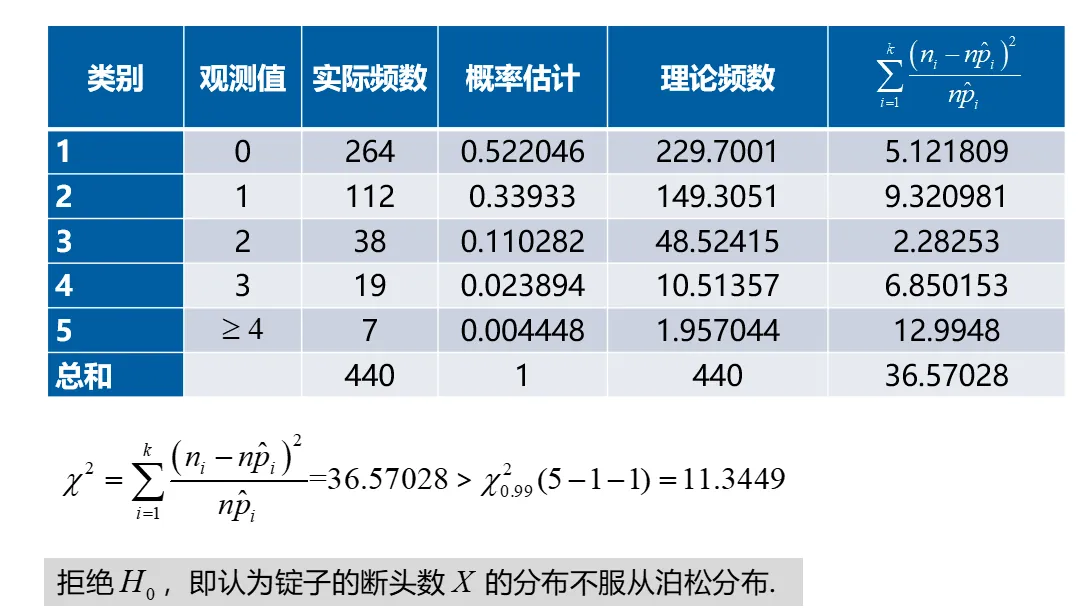
在上面这个例子中,我们假定每一组 {X=i} 的概率值 pi 都是已知的 i=1,2,⋯,k ,但在实际问题中,有时 pi 还依赖于 r 个未知参数,而这 r 个未知参数需要利用样本来估计,这时,我们先用点估计法估计出这 r 个未知参数,然后再算出 pi 的估计值 p^i 。类似于式(8-1),定义检验统计量
χ2=i=1∑knp^i(Ni−np^i)2 当样本量 n→∞ 时, 费希尔在 1924 年证明了, 式 (8-2) 还是渐近服从 χ2 分布, 但是自由度为 k−r−1, 即
χ2=i=1∑knp^i(Ni−np^i)2∼χ2(k−r−1). 故此时,拒绝域为
W={i=1∑knp^i(Ni−np^i)2>χ1−α2(k−r−1)}. 





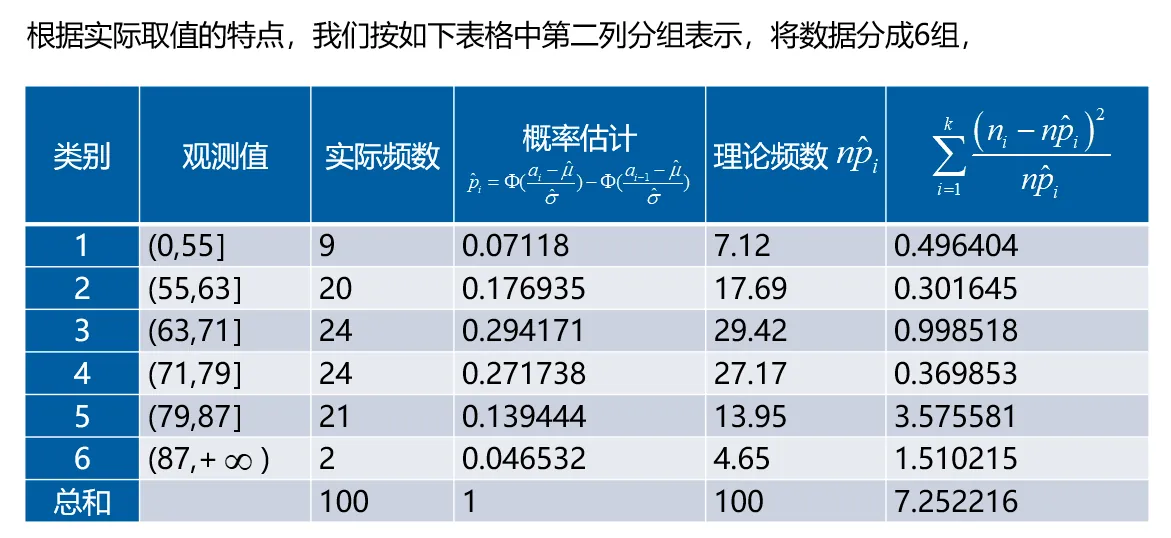
 当总体 X 是连续型的随机变量,分布函数为 F(x) ,选 k−1 个实数 a1<a2<⋯<ak−1 , 将实数轴分为 k 个区间
当总体 X 是连续型的随机变量,分布函数为 F(x) ,选 k−1 个实数 a1<a2<⋯<ak−1 , 将实数轴分为 k 个区间
(−∞,a1],(a1,a2],⋯(ak−1,+∞) 当观测值落在第 i 个区间内,就把这个观测值看作是属于第 i 类,因此, 这 k 个区间就相 当于是 k 个类。在 H0 成立时,记
pi=P(ai−1<X≤ai)=F(ai)−F(ai−1),i=1,2,…,r 其中 a0=−∞,ar=+∞ , 以 ni 表示样本观测值 x1,⋯…,xn 落在区间 (ai−1,at 内的个数 (i=1,2,…,r)
之后的求解过程与总体只取有限个值的情况一样。









 当总体 是连续型的随机变量,分布函数为 ,选 个实数 , 将实数轴分为 个区间
当总体 是连续型的随机变量,分布函数为 ,选 个实数 , 将实数轴分为 个区间


