4.2_数值微分的实现
4.2 数值微分的实现
下面根据导数的定义式,即式子4.1来实现求导。需要注意的是,计算机不能处理极限值。因此,这里的 表示一个近似值。例如我们可以用 这种非常小的值来计算式子4.1。利用微小的差值获得函数变化量的方法叫作数值微分。
数值微分使用非常小的值 求出的是真的导数的近似值。因此,这个值
包含误差。中心差分近似是减小近似值误差的一种方法。中心差分近似计算的不是 和 的差,而是 和 的差。图4-2中的粗线表示的就是中心差分近似。
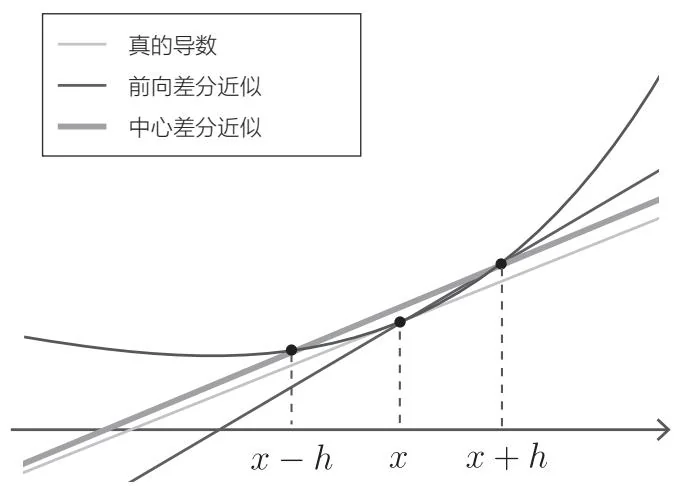
图4-2 比较真的导数、前向差分近似和中心差分近似
如图4-2所示,计算过 和 这两点的直线的斜率的方法称为前向差分近似,计算 和 这两点间斜率的方法称为中心差分近似,中心差分近似实际产生的误差更小。这一点的证明超出了本书的范围,不过我们从图4-2中直线的斜率可以直观地得出这个结论。中心差分近似的直线斜率为 (注意分母是 )。

中心差分近似比前向差分近似更接近真的导数这个结论可以通过泰勒展开来证明。相关证明过程请阅读参考文献[1]等资料。
下面我们来实现使用中心差分近似求数值微分的函数,该函数的名称为
numerical_diff(f, x, eps=1e-4)。这里的参数f是被求导的函数,是Function类的实例。参数x为求导的变量,是Variable类的实例。参数eps代表一个微小的值,默认值是1e-4①(eps是epsilon的缩写)。数值微分可通过以下代码实现。
steps/step04.py
def numerical_diff(f, x, eps=1e-4):
x0 = Variable(x.data - eps)
x1 = Variable(x.data + eps)
y0 = f(x0)
y1 = f(x1)
return (y1.data - y0.data) / (2 * eps)只要注意Variable实例变量data中包含实际数据即可。下面我们使用这个函数求步骤3中实现的Square类的导数。
steps/step04.py
f = Square()
x = Variable(np.array(2.0))
dy = numerical_diff(f, x)
print(dy)运行结果
4.000000000004
由上面的运行结果可知, 在 时计算得到的导数值为4.000000000004。不包含误差的导数值是4.0,可以说这个结果大体正确。

导数也可以通过解析解的方式求解。解析解的方式求解是指只通过式子的变形推导出答案。在上面的例子中,根据导数的公式可知, 的导数为 是 对 求导的符号)。因此, 在 处的导数为4.0。这个4.0是不包含误差的值。前面的数值微分结果虽然不是正好为4.0,但我们可以看出误差是相当小的。