0x5A_斜率优化
0x5A斜率优化
在上一节末尾我们给出了动态规划的一个经典模型 ,并总结了单调队列优化的基本条件——多项式 的每一项仅与 和 中的一个有关。在本节中,我们将讨论多项式 包含 的乘积项,即存在一个同时与 和 有关的部分时,该如何进行优化。
【例题】任务安排1 TYVJ1098
有 个任务排成一个序列在一台机器上等待执行,它们的顺序不得改变。机器会把这 个任务分成若干批,每一批包含连续的若干个任务。从时刻0开始,任务被分批加工,执行第 个任务所需的时间是 。另外,在每批任务开始前,机器需要 的启动时间,故执行一批任务所需的时间是启动时间 加上每个任务所需时间之和。
一个任务执行后,将在机器中稍作等待,直至该批任务全部执行完毕。也就是说,同一批任务将在同一时刻完成。每个任务的费用是它的完成时刻乘以一个费用系数 。请为机器规划一个分组方案,使得总费用最小。
数据范围:
解法一
求出 的前缀和 ,即 , 。设 表示把前 个任务分成 批执行的最小费用,则第 批任务完成的时间就是 。以第 批和第 批任务的分界点为 DP 的“决策”,状态转移方程为:
该解法的时间复杂度为 。
解法二
本题并没有规定需要把任务分成多少批,在上一个解法中之所以需要批数 ,是因为我们需要知道机器启动了多少次(每次启动都要 单位时间),从而计算出 所在的一批任务的完成时刻。
事实上,在执行一批任务时,我们不容易直接得知在此之前机器启动过几次。但我们知道,机器因执行这批任务而花费的启动时间 ,会累加到在此之后所有任务的完成时刻上。设 表示把前 个任务分成若干批执行的最小费用,状态转移方程为:
在上式中,第 个任务在同一批内完成,sumT[i] 是忽略机器的启动时间时,这批任务的完成时刻。因为这批任务的执行,机器的启动时间 会对第 个之后的所有任务产生影响,故我们把这部分补充到费用中。
也就是说,我们没有直接求出每批任务的完成时刻,而是在一批任务“开始”对后续任务产生影响时,就先把费用累加到答案中。这是一种名为“费用提前计算”的经典思想。
该解法的时间复杂度为 。
long long f[5010], sumt[5010], sumc[5010];
int n, s;
int main() {
cin >> n >> s;
for (int i = 1; i <= n; i++) {
int t, c;
scanf("%d%d", &t, &c);
sumt[i] = sumt[i - 1] + t;
sumc[i] = sumc[i - 1] + c;
}
memset(f, 0x3f, sizeof(f));
f[0] = 0;
for (int i = 1; i <= n; i++) {
for (int j = 0; j < i; j++)
f[i] = min(f[i], f[j] + sumt[i] * (sumc[i] - sumc[j]) + s*(sumc[n] - sumc[j]);
cout << f[n] << endl;
}【例题】任务安排2IOI2002/POJ1180
题意同“任务安排1”。
数据范围:
对上一题的解法二进行优化,先对状态转移方程稍作变形,把常数、仅与 有关的项、仅与 有关的项以及 的乘积项分开。
把min函数去掉,把关于 的值 和sumC[j]看作变量,其余部分看作常
数,得到:
在 为横坐标, 为纵坐标的平面直角坐标系中,这是一条以 为斜率, 为截距的直线。也就是说,决策候选集合是坐标系中的一个点集,每个决策 都对应着坐标系中的一个点 。每个待求解的状态 都对应着一条直线的截距,直线的斜率是一个固定的值 ,截距未知。当截距最小化时, 也取到最小值。
该问题实际上是一个线性规划问题,高中数学课本中应该有所涉及。令直线过每个决策点 ,都可以解出一个截距,其中使截距最小的一个就是最优决策。体现在坐标系中,就是用一条斜率为固定正整数的直线自下而上平移,第一次接触到某个决策点时,就得到了最小截距。如下图所示:
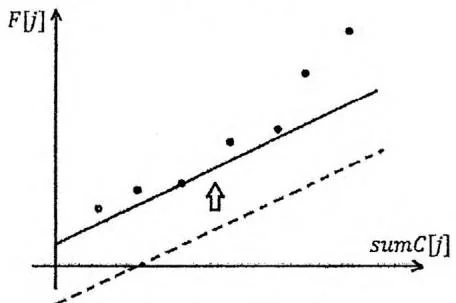
对于任意三个决策点 , 和 ,不妨设 ,因为 均为正整数,亦有 。根据“及时排除无用决策”的思想,我们来考虑 有可能成为最优决策的条件。
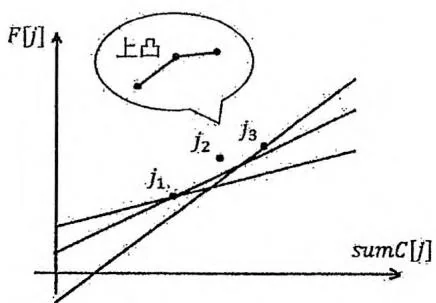
连接 的线段与连接 的线段构成上凸形状无论直线斜率是多少, 都不是最优决策
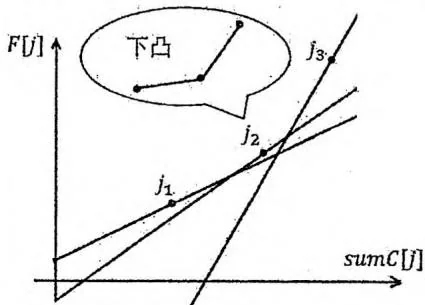
连接 的线段与连接 的线段构成下凸形状 有可能成为最优决策
从上图中我们发现, 有可能成为最优决策,当且仅当:
不等号两侧实际上都是连接两个决策点的线段的斜率。通俗地讲,我们应该维护
“连接相邻两点的线段斜率”单调递增的一个“下凸壳”①,只有这个“下凸壳”的顶点才有可能成为最优决策。实际上,对于一条斜率为 的直线,若某个顶点左侧线段的斜率比 小、右侧线段的斜率比 大,则该顶点就是最优决策。换言之,如果把这条直线和所有线段组成一个序列,那么令直线截距最小化的顶点就出现在按照斜率大小排序时,直线应该排在的位置上。如下图所示:
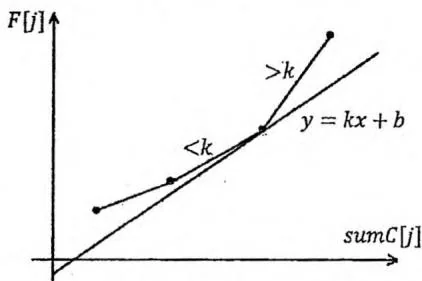
在本题中, 的取值范围是 ,随着 的增大,每次会有一个新的决策进入候选集合。因为sumC的单调性,新决策在坐标系中的横坐标一定大于之前的所有决策,出现在整个凸壳的最右端。另外,因为sumT的单调性,每次求解“最小截距”的直线斜率 也单调递增,如果我们只保留凸壳上“连接相邻两点的线段斜率”大于 的部分,那么凸壳的最左端顶点就一定是最优决策。
综上所述,我们可以建立单调队列 ,维护这个下凸壳。队列中保存若干个决策变量,它们对应凸壳上的顶点,且满足横坐标sumC递增、连接相邻两点的线段斜率也递增。需要支持的操作与一般的单调队列题目类似,对于每个状态变量
检查队头的两个决策变量 和 ,若斜率 \left(F[q[l + 1] - F[q[l]}\right)/\left(sumC[q[l + 1]] - sumC[q[l]]\right) \leq S + sumT[i] ,则把 出队,继续检查新的队头。
直接取队头 为最优决策,执行状态转移,计算出 。
把新决策 从队尾插入,在插入之前,若三个决策点 不满足斜率单调递增(不满足下凸性,即 是无用决策),则直接从队尾把 出队,继续检查新的队尾。
整个算法的时间复杂度为 。
int main() { cin >> n >> s; for (int i = 1; i <= n; i++) {int t, c;
scanf("%d%d", &t, &c);
sumt[i] = sumt[i - 1] + t;
sumc[i] = sumc[i - 1] + c;
}
memset(f, 0x3f, sizeof(f));
f[0] = 0;
int l = 1, r = 1;
q[1] = 0;
for (int i = 1; i <= n; i++) {
while (l < r && (f[q[l+1]] - f[q[l]])
<= (s + sumt[i]) * (sumc[q[l+1]] - sumc[q[l]])) l++;
f[i] = f[q[l]] - (s + sumt[i]) * sumc[q[l]]
+ sumt[i] * sumc[i] + s * sumc[n];
while (l < r && (f[q[r]] - f[q[r-1]]) * (sumc[i] - sumc[q[r]])
>= (f[i] - f[q[r]]) * (sumc[q[r]] - sumc[q[r-1]])) r--;
q[++r] = i;
}
cout << f[n] << endl;
}与一般的单调队列优化DP的模型相比,本题维护的“单调性”依赖于队列中相邻两个元素之间的某种“比值”。因为这个值对应线性规划的坐标系中的斜率,所以我们把本题中使用的优化方法称为“斜率优化”,英文称为convex hull trick(直译为凸壳优化策略)。
*【例题】任务安排3BZOJ2726
题意同“任务安排1”。
数据范围:
与上一题不同的是,任务的执行时间 可能是负数。这意味着 不具有单调性,从而需要最小化截距的直线的斜率 不具有单调性。所以,我们不能在单调队列中只保留凸壳上“连接相邻两点的线段斜率”大于 的部分,而是必须维护整个凸壳。这样一来,我们就不需要在队头把斜率与 比较。
队头也不一定是最优决策,我们可以在单调队列中二分查找,求出一个位置 , 左侧线段的斜率比 小,右侧线段的斜率比 大, 就是最优决策。
队尾维护斜率单调性的方法与上一题相同。
int binary_search(int i, int k) {
if (l == r) return q[l];
int L = l, R = r;
while (L < R) {
int mid = (L + R) >> 1;
if (f[q[mid + 1]] - f[q[mid]] <= k *
(sumc[q[mid + 1]] - sumc[q[mid]])) L = mid + 1;
else R = mid;
}
return q[L];
}*【思考题】任务安排4
如果 是正整数,但 可能是负数,该怎么办?
如果 和 都有可能是负数呢?
提示:
若 可能是负数,可以倒序DP,设计一个状态转移方程,让sumT是横坐标,
sumC是斜率中的一项。仍然可以用单调队列维护凸壳,用二分法求出最优决策。
若二者都可能是负数,则意味着要在凸壳任意位置动态插入顶点、动态查询。此时要用平衡树来维护凸壳。
【例题】Cats Transport Codeforces311B
小S是农场主,他养了M只猫,雇了P位饲养员。农场中有一条笔直的路,路边有N座山,从1到N编号。第i座山与第i-1座山之间的距离是Di。饲养员都住在1号山。
有一天,猫出去玩。第 只猫去 号山玩,玩到时刻 停止,然后在原地等饲养员来接。饲养员们必须回收所有的猫。每个饲养员沿着路从1号山走到 号山,把各座山上已经在等待的猫全部接走。饲养员在路上行走需要时间,速度为1米/单位时间。饲养员在每座山上接猫的时间可以忽略,可以携带的猫的数量为无穷大。
例如有两座相距为1的山,一只猫在2号山玩,玩到时刻3开始等待。如果饲养员从1号山在时刻2或3出发,那么他可以接到猫,猫的等待时间为0或1。而如果他于时刻1出发,那么他将于时刻2经过2号山,不能接到当时仍在玩的猫。
你的任务是规划每个饲养员从1号山出发的时间,使得所有猫等待时间的总和尽量小。饲养员出发的时间可以为负。
数据范围:
对于每只猫,设 。一名饲养员如果想接到第 只猫,就必须在 时刻之后从1号山出发。若出发时刻为 ,则这只猫的等待时间就是 。
把 从小到大排序,求出排好序的 数组的前缀和,记录在数组 中。根据贪心策略,每个饲养员带走的猫一定是按照 排序后连续的若干只,请读者尝试给出证明,这里就不再赘述。
此时本题就与“任务安排”非常类似。饲养员就是“机器”,猫就是“任务”,每个饲养员带走连续的一段猫。设 表示前 个饲养员带走前 只猫,猫等待时间的总和最小是多少。
假设第 个饲养员带走第 只猫,那么该饲养员的最早出发时间就是 。这些猫的等待时间之和就是 。写出状态转移方程:
直接枚举 ,求出 的最小值,时间复杂度为 。
把外层循环 看作定值, 是状态变量, 是决策变量。方程中存在乘积项 ,应考虑使用斜率优化。去掉 函数,对方程进行移项,等号左边放仅与 有关的项,等号右边放 乘积项以及仅与 有关的项:
以 为横坐标, 为纵坐标建立平面直角坐标系。上式是一条以 为斜率, 为截距的直线,当截距最小化时, 取到最小值。
在最小化截距的线性规划问题中,应维护一个下凸壳。建立一个单调队列,队列中相邻两个决策 和 应满足 并且“斜率” 单调递增。因为直线斜率 也已经从小到大排过序,所以在程序实现中,采用与“任务安排2”类似的单调队列的三个基本操作即可。