0x51 线性 DP 在本书中,具有线性“阶段”划分的动态规划算法被统称为线性 D P ① \mathrm{DP}^{\text{①}} DP ①
容易发现,无论状态表示是一维还是多维,DP算法在这些问题上都体现为“作用
在线性空间上的递推”——DP的阶段沿着各个维度线性增长,从一个或多个“边界点”开始有方向地向整个状态空间转移、扩展,最后每个状态上都保留了以自身为“目标”的子问题的最优解。
这几个问题也是线性DP中最简单的一类,在这类问题中,需要计算的对象表现出明显的维度以及有序性,每个状态的求解直接构成一个阶段,这使得DP的状态表示就是阶段的表示。因此,我们只需要在每个维度上各取一个坐标值作为DP的状态,自然就可以描绘出“已求解部分”在状态空间中的轮廓特征,该轮廓的进展就是阶段的推移。另外,每个状态的求解显然只与之前阶段的最优解有关,最优子结构性质也得以验证。接下来,我们按顺序依次循环每个维度,根据问题要求递推求解的具体实现过程也就顺理成章了。
【例题】Mr. Young's Picture Permutations POJ2279 有 N N N k k k N 1 , N 2 , … , N k N_{1}, N_{2}, \dots, N_{k} N 1 , N 2 , … , N k k k k 1 , 2 , … , N 1, 2, \dots, N 1 , 2 , … , N N ≤ 30 , k ≤ 5 N \leq 30, k \leq 5 N ≤ 30 , k ≤ 5
下面的一排三角矩阵给出了当 N = 6 , k = 3 , N 1 = 3 , N 2 = 2 , N 3 = 1 N = 6, k = 3, N_1 = 3, N_2 = 2, N_3 = 1 N = 6 , k = 3 , N 1 = 3 , N 2 = 2 , N 3 = 1
因为在合法的合影方案中每行、每列的身高都是单调的,所以我们可以从高到低依次考虑标记为 1 , 2 , … , N 1,2,\dots ,N 1 , 2 , … , N k k k ( a 1 , a 2 , … , a k ) (a_{1},a_{2},\dots ,a_{k}) ( a 1 , a 2 , … , a k )
当安排一名新的学生时,我们考虑所有满足如下条件的行号 i i i
a i < N i a_{i} < N_{i} a i < N i
i = 1 i = 1 i = 1 a i − 1 > a i a_{i - 1} > a_i a i − 1 > a i
只要该学生站在这样一行中,每列学生的身高单调性也就得以满足。换言之,我们不需要关心已经站好的 ( a 1 + a 2 + ⋯ + a k ) (a_{1} + a_{2} + \dots + a_{k}) ( a 1 + a 2 + ⋯ + a k ) k k k ( a 1 , a 2 , … , a k ) (a_{1}, a_{2}, \dots, a_{k}) ( a 1 , a 2 , … , a k ) a 1 , a 2 , … , a k a_{1}, a_{2}, \dots, a_{k} a 1 , a 2 , … , a k a 1 , a 2 , … , a k a_{1}, a_{2}, \dots, a_{k} a 1 , a 2 , … , a k
简便起见,我们假设 k = 5 k = 5 k = 5 k < 5 k < 5 k < 5
价于 k = 5 k = 5 k = 5
F [ a 1 , a 2 , a 3 , a 4 , a 5 ] F[a_{1},a_{2},a_{3},a_{4},a_{5}] F [ a 1 , a 2 , a 3 , a 4 , a 5 ] a 1 , a 2 , a 3 , a 4 , a 5 a_1,a_2,a_3,a_4,a_5 a 1 , a 2 , a 3 , a 4 , a 5
边界: F [ 0 , 0 , 0 , 0 , 0 ] = 1 F[0,0,0,0,0] = 1 F [ 0 , 0 , 0 , 0 , 0 ] = 1
目标: F [ N 1 , N 2 , N 3 , N 4 , N 5 ] F[N_{1},N_{2},N_{3},N_{4},N_{5}] F [ N 1 , N 2 , N 3 , N 4 , N 5 ]
转移:若 a 1 < N 1 a_1 < N_1 a 1 < N 1 F [ a 1 + 1 , a 2 , a 3 , a 4 , a 5 ] + = F [ a 1 , a 2 , a 3 , a 4 , a 5 ] F[a_1 + 1, a_2, a_3, a_4, a_5] + = F[a_1, a_2, a_3, a_4, a_5] F [ a 1 + 1 , a 2 , a 3 , a 4 , a 5 ] + = F [ a 1 , a 2 , a 3 , a 4 , a 5 ] a 2 < N 2 a_2 < N_2 a 2 < N 2 a 1 > a 2 a_1 > a_2 a 1 > a 2 F [ a 1 , a 2 + 1 , a 3 , a 4 , a 5 ] + = F [ a 1 , a 2 , a 3 , a 4 , a 5 ] F[a_1, a_2 + 1, a_3, a_4, a_5] + = F[a_1, a_2, a_3, a_4, a_5] F [ a 1 , a 2 + 1 , a 3 , a 4 , a 5 ] + = F [ a 1 , a 2 , a 3 , a 4 , a 5 ] 3 ∼ 5 3 \sim 5 3 ∼ 5
本题还有一种数学解法:直接用“杨氏矩阵”和“勾长公式”进行计算。这里就不再赘述,感兴趣的读者可以查阅相关资料。
从该题给出的解法中我们发现,设计动态规划的状态转移方程,不一定要以“如何计算出一个状态”的形式给出,也可以考虑“一个已知状态应该更新哪些后续阶段的未知状态”。当然,对于本题来讲,两种方式没有什么差别。在有的题目中,其中一种可能会比另一种思考起来更加自然、简便。
【例题】LCIS(最长公共上升子序列)TYVJ1071
熊大妈的奶牛在小沐沐的熏陶下开始研究信息题目。小沐沐先让奶牛研究了最长上升子序列,再让他们研究了最长公共子序列,现在又让他们研究最长公共上升子序列了。
小沐沐说,对于两个数列 A A A B B B
奶牛半懂不懂,小沐沐要你来告诉奶牛什么是最长公共上升子序列。不过,只要告诉奶牛它的长度就可以了。数列 A A A B B B
这道题目是LIS与LCS的综合。请读者回顾在本节开头部分列举的LIS与LCS问题的动态规划状态表示,把二者相结合,容易想到以下解法:
F [ i , j ] F[i,j] F [ i , j ] A 1 ∼ A i A_{1} \sim A_{i} A 1 ∼ A i B 1 ∼ B j B_{1} \sim B_{j} B 1 ∼ B j B j B_{j} B j A 0 = B 0 = − ∞ A_{0} = B_{0} = -\infty A 0 = B 0 = − ∞
当 A i ≠ B j A_{i}\neq B_{j} A i = B j F [ i , j ] = F [ i − 1 , j ] F[i,j] = F[i - 1,j] F [ i , j ] = F [ i − 1 , j ]
当 A i = B j A_{i} = B_{j} A i = B j
F [ i , j ] = max 0 ≤ k < j , B k < B j { F [ i − 1 , k ] } + 1 = max 0 ≤ k < j , B k < A i { F [ i − 1 , k ] } + 1 F [ i, j ] = \max _ {0 \leq k < j, B _ {k} < B _ {j}} \{F [ i - 1, k ] \} + 1 = \max _ {0 \leq k < j, B _ {k} < A _ {i}} \{F [ i - 1, k ] \} + 1 F [ i , j ] = 0 ≤ k < j , B k < B j max { F [ i − 1 , k ]} + 1 = 0 ≤ k < j , B k < A i max { F [ i − 1 , k ]} + 1 显然,上面的状态转移方程可以直接用三重循环的程序计算(初始化部分省略)。
f o r ( i n t i = 1 ; i < = n ; i + + ) f o r (i n t i = 1; i < = n; i + +) f or ( in t i = 1 ; i <= n ; i + + ) f o r ( i n t j = 1 ; j < = m ; j + + ) f o r (i n t j = 1; j < = m; j + +) f or ( in t j = 1 ; j <= m ; j + + ) if $(a[i] == b[j])$ { for(int $k = 0;k < j;k + + )$ if $(b[k] < a[i])$ (20 $f[i][j] = \max (f[i][j],f[i - 1][k] + 1);$ 1} else $f[i][j] = f[i - 1][j];$在转移过程中,我们把满足 0 ≤ k < j , B k < A i 0 \leq k < j, B_{k} < A_{i} 0 ≤ k < j , B k < A i k k k F [ i , j ] F[i,j] F [ i , j ] S ( i , j ) S(i,j) S ( i , j ) j j j m m m i i i B k < A i B_{k} < A_{i} B k < A i j j j k k k 0 ≤ k < j 0 \leq k < j 0 ≤ k < j 0 ≤ k < j + 1 0 \leq k < j + 1 0 ≤ k < j + 1 j j j B j < A i B_{j} < A_{i} B j < A i
S ( i , j + 1 ) = { S ( i , j ) B j ≥ A i S ( i , j ) ∪ { j } B j < A i S (i, j + 1) = \left\{ \begin{array}{l l} S (i, j) & B _ {j} \geq A _ {i} \\ S (i, j) \cup \{j \} & B _ {j} < A _ {i} \end{array} \right. S ( i , j + 1 ) = { S ( i , j ) S ( i , j ) ∪ { j } B j ≥ A i B j < A i 所以,上面的状态转移方程只需要两重循环即可求解。
for (int i = 1; i <= n; i++) { // val 是决策集合 S(i, j) 中 f[i-1][k] 的最大值 int val = 0; // j=1 时,0 可以作为 k 的取值 if (b[0] < a[i]) val = f[i - 1][0]; for (int j = 1; j <= m; j++) { if (a[i] == b[j]) f[i][j] = val + 1; else f[i][j] = f[i - 1][j]; // j 即将增大为 j+1,检查 j 能否进入新的决策集合 if (b[j] < a[i]) val = max(val, f[i - 1][j]); }这道题转移部分的优化告诉我们,在实现状态转移方程时,要注意观察决策集合的范围随着状态的变化情况。对于“决策集合中的元素只增多不减少”的情景,就可以像本题一样维护一个变量来记录决策集合的当前信息,避免重复扫描,把转移的复杂度降低一个量级。
【例题】Making the Grade FOJ3666 给定长度为 N N N A A A N N N B B B
B B B B 1 ≤ B 2 ≤ ⋯ ≤ B N B_{1} \leq B_{2} \leq \dots \leq B_{N} B 1 ≤ B 2 ≤ ⋯ ≤ B N B 1 ≥ B 2 ≥ ⋯ ≥ B N B_{1} \geq B_{2} \geq \dots \geq B_{N} B 1 ≥ B 2 ≥ ⋯ ≥ B N
最小化 S = ∑ i = 1 N ∣ A i − B i ∣ S = \sum_{i=1}^{N} |A_i - B_i| S = ∑ i = 1 N ∣ A i − B i ∣
只需要求出这个最小值 S S S 1 ≤ N ≤ 2000 , 1 ≤ ∣ A i ∣ ≤ 10 9 1 \leq N \leq 2000, 1 \leq |A_i| \leq 10^9 1 ≤ N ≤ 2000 , 1 ≤ ∣ A i ∣ ≤ 1 0 9
序列 B B B
引理
在满足 S S S B B B B B B A A A
证明:
数学归纳法。命题对 N = 1 N = 1 N = 1
设引理对 N = k − 1 N = k - 1 N = k − 1 B 1 ∼ B k − 1 B_{1} \sim B_{k - 1} B 1 ∼ B k − 1
当 N = k N = k N = k B k − 1 ≤ A k B_{k - 1}\leq A_k B k − 1 ≤ A k B k = A k B_{k} = A_{k} B k = A k
否则,要么令 B k = B k − 1 B_{k} = B_{k - 1} B k = B k − 1 j j j B j , B j + 1 , … , B k B_{j},B_{j + 1},\dots ,B_{k} B j , B j + 1 , … , B k V \mathcal{V} V A j , A j + 1 , … , A k A_{j},A_{j + 1},\dots ,A_{k} A j , A j + 1 , … , A k m i d ≥ B j − 1 mid\geq B_{j - 1} mi d ≥ B j − 1 v = m i d v = mid v = mi d v = B j − 1 v = B_{j - 1} v = B j − 1 B 1 ∼ B k B_{1}\sim B_{k} B 1 ∼ B k A A A
证毕。
回到本题。我们依次考虑:完成前 i ( 1 ≤ i ≤ N ) i(1 \leq i \leq N) i ( 1 ≤ i ≤ N ) ∑ j = 1 i ∣ A j − B j ∣ \sum_{j=1}^{i} |A_j - B_j| ∑ j = 1 i ∣ A j − B j ∣ B i B_i B i B i − 1 B_{i-1} B i − 1
方法一
仿照LIS问题,设 F [ i ] F[i] F [ i ] i i i B i = A i B_{i} = A_{i} B i = A i S S S
F [ i ] = min 0 ≤ j < i , A [ j ] ≤ A [ i ] { F [ j ] + c o s t ( j + 1 , i − 1 ) } F [ i ] = \min _ {0 \leq j < i, A [ j ] \leq A [ i ]} \{F [ j ] + c o s t (j + 1, i - 1) \} F [ i ] = 0 ≤ j < i , A [ j ] ≤ A [ i ] min { F [ j ] + cos t ( j + 1 , i − 1 )} 其中, c o s t ( j + 1 , i − 1 ) cost(j + 1, i - 1) cos t ( j + 1 , i − 1 ) B j + 1 , … , B i − 1 B_{j+1}, \dots, B_{i-1} B j + 1 , … , B i − 1 A j ≤ B j + 1 ≤ ⋯ ≤ B i − 1 ≤ A i A_j \leq B_{j+1} \leq \dots \leq B_{i-1} \leq A_i A j ≤ B j + 1 ≤ ⋯ ≤ B i − 1 ≤ A i ∑ k = j + 1 i − 1 ∣ A k − B k ∣ \sum_{k=j+1}^{i-1} |A_k - B_k| ∑ k = j + 1 i − 1 ∣ A k − B k ∣
该解法的思路是,根据引理可知,最终 B B B A A A i i i A A A j j j cost ( j + 1 , i − 1 ) \operatorname{cost}(j + 1, i - 1) cost ( j + 1 , i − 1 ) [ j + 1 , i − 1 ] [j + 1, i - 1] [ j + 1 , i − 1 ] A j A_j A j A i A_i A i
注意,我们不需要考虑存在一个 k ∈ [ j + 1 , i − 1 ] k \in [j + 1, i - 1] k ∈ [ j + 1 , i − 1 ] [ j + 1 , i − 1 ] [j + 1, i - 1] [ j + 1 , i − 1 ] A k A_k A k j = k j = k j = k
采用朴素算法计算cost值,总的时间复杂度为 O ( N 3 ) O(N^3) O ( N 3 )
方法二 既然仅把DP的“阶段”要素(即已经处理的序列长度)放在DP状态中不足以执行转移,一个直接的想法就是把 B B B F [ i , j ] F[i,j] F [ i , j ] i i i B i = j B_{i} = j B i = j S S S
F [ i , j ] = min 0 ≤ k ≤ j { F [ i − 1 , k ] + ∣ A i − j ∣ } F [ i, j ] = \min _ {0 \leq k \leq j} \left\{F [ i - 1, k ] + | A _ {i} - j | \right\} F [ i , j ] = 0 ≤ k ≤ j min { F [ i − 1 , k ] + ∣ A i − j ∣ } 根据引理,我们可以把 A A A j j j O ( N ) O(N) O ( N ) O ( N 2 ) O(N^{2}) O ( N 2 )
【思考题】 把一个序列 A A A
提示:序列 A A A A A A
把一个序列 A A A
提示:构造序列 B [ i ] = A [ i ] − i B[i] = A[i] - i B [ i ] = A [ i ] − i B B B
请读者思考:为什么这样是正确的?为什么用序列总长度减去 A A A
【例题】Mobile Service TYVJ1061 一个公司有三个移动服务员,最初分别在位置1,2,3处。
如果某个位置 (用一个整数表示) 有一个请求, 那么公司必须指派某名员工赶到那个地方去。某一时刻只有一个员工能移动, 且不允许在同样的位置出现两个员工。从 p p p q q q c ( p , q ) c\left( {p,q}\right) c ( p , q ) c ( p , p ) = 0 c\left( {p,p}\right) = 0 c ( p , p ) = 0
给出 N N N p 1 ∼ p N p_1 \sim p_N p 1 ∼ p N N ≤ 1000 N \leq 1000 N ≤ 1000 1 ∼ 200 1 \sim 200 1 ∼ 200
使用动态规划解决本题,容易发现DP的“阶段”就是“已经完成的请求数量”,通过指派一名服务员,可以把一个“完成 i − 1 i - 1 i − 1 i i i
为了计算指派服务员的花费,就必须要知道状态转移时每个服务员的位置。最直接的想法就是把三个服务员的位置也放在DP的“状态”中。设 F [ i , x , y , z ] F[i, x, y, z] F [ i , x , y , z ]
了前 i i i x , y , z x, y, z x , y , z
考虑 F [ i , x , y , z ] F[i, x, y, z] F [ i , x , y , z ] i + 1 i + 1 i + 1 i + 1 i + 1 i + 1
F [ i + 1 , p i + 1 , y , z ] = min ( F [ i + 1 , p i + 1 , y , z ] , F [ i , x , y , z ] + c ( x , p i + 1 ) ) F [ i + 1, p _ {i + 1}, y, z ] = \min \left(F [ i + 1, p _ {i + 1}, y, z ], F [ i, x, y, z ] + c (x, p _ {i + 1})\right) F [ i + 1 , p i + 1 , y , z ] = min ( F [ i + 1 , p i + 1 , y , z ] , F [ i , x , y , z ] + c ( x , p i + 1 ) ) F [ i + 1 , x , p i + 1 , z ] = min ( F [ i + 1 , x , p i + 1 , z ] , F [ i , x , y , z ] + c ( y , p i + 1 ) ) F [ i + 1, x, p _ {i + 1}, z ] = \min \left(F [ i + 1, x, p _ {i + 1}, z ], F [ i, x, y, z ] + c (y, p _ {i + 1})\right) F [ i + 1 , x , p i + 1 , z ] = min ( F [ i + 1 , x , p i + 1 , z ] , F [ i , x , y , z ] + c ( y , p i + 1 ) ) F [ i + 1 , x , y , p i + 1 ] = min ( F [ i + 1 , x , y , p i + 1 ] , F [ i , x , y , z ] + c ( z , p i + 1 ) ) F [ i + 1, x, y, p _ {i + 1} ] = \min \left(F [ i + 1, x, y, p _ {i + 1} ], F [ i, x, y, z ] + c (z, p _ {i + 1})\right) F [ i + 1 , x , y , p i + 1 ] = min ( F [ i + 1 , x , y , p i + 1 ] , F [ i , x , y , z ] + c ( z , p i + 1 ) ) 该算法的规模大约在 1000 ∗ 200 3 1000 * 200^{3} 1000 ∗ 20 0 3 i i i p i p_{i} p i i i i p i p_{i} p i
因此,可用 F [ i , x , y ] F[i, x, y] F [ i , x , y ] i i i p i p_i p i x x x y y y
三种转移则分别是让位于 p i , x p_i, x p i , x y y y p i + 1 p_{i+1} p i + 1
F [ i + 1 , x , y ] = min ( F [ i + 1 , x , y ] , F [ i , x , y ] + c ( p i , p i + 1 ) ) F [ i + 1, x, y ] = \min \left(F [ i + 1, x, y ], F [ i, x, y ] + c \left(p _ {i}, p _ {i + 1}\right)\right) F [ i + 1 , x , y ] = min ( F [ i + 1 , x , y ] , F [ i , x , y ] + c ( p i , p i + 1 ) ) F [ i + 1 , p i , y ] = min ( F [ i + 1 , p i , y ] , F [ i , x , y ] + c ( x , p i + 1 ) ) F [ i + 1, p _ {i}, y ] = \min \left(F [ i + 1, p _ {i}, y ], F [ i, x, y ] + c (x, p _ {i + 1})\right) F [ i + 1 , p i , y ] = min ( F [ i + 1 , p i , y ] , F [ i , x , y ] + c ( x , p i + 1 ) ) F [ i + 1 , x , p i ] = min ( F [ i + 1 , x , p i ] , F [ i , x , y ] + c ( y , p i + 1 ) ) F [ i + 1, x, p _ {i} ] = \min \left(F [ i + 1, x, p _ {i} ], F [ i, x, y ] + c (y, p _ {i + 1})\right) F [ i + 1 , x , p i ] = min ( F [ i + 1 , x , p i ] , F [ i , x , y ] + c ( y , p i + 1 ) ) 不妨设 p 0 = 3 p_0 = 3 p 0 = 3 F [ 0 , 1 , 2 ] = 0 F[0,1,2] = 0 F [ 0 , 1 , 2 ] = 0 F [ N , ? , ? ] F[N,?,?] F [ N , ? , ?]
这道题给我们两点启发:
求解线性DP问题,一般先确定“阶段”。若“阶段”不足以表示一个状态,则可以把所需的附加信息也作为状态的维度。
在转移时,若总是从一个阶段转移到下一个阶段(本题 i i i i + 1 i + 1 i + 1 x , y , z x, y, z x , y , z
在确定 DP 状态时,要选择最小的能够覆盖整个状态空间的“维度集合”。
若DP状态由多个维度构成,则应检查这些维度之间能否相互导出,用尽量少的维度覆盖整个状态空间,排除冗余维度。可以类比第0x36节中提到的“线性无关组”。例如本题,阶段 i i i
【例题】传纸条 NOIP2008/CODEVS1169 给定一个 N ∗ M N * M N ∗ M A A A ( N , M ) (N, M) ( N , M ) N , M ≤ 50 N, M \leq 50 N , M ≤ 50
首先尝试寻找一个线性的“阶段”。考虑路径形成的过程,我们需要从左上角开始依次确定两条路径上的每一步如何走,直至到达右下角。把路径与前面问题中的序列相类比,自然想到可以把“路径长度”,即当前走过的步数,作为DP的“阶段”。在每个阶段中,我们把两条路径同时扩展一步,路径长度增加1,从而转移到下一个阶段。
除了“路径长度”外,还需要确定两条路径当前的末尾位置。设路径长度为 i i i ( x 1 , y 1 ) (x_{1},y_{1}) ( x 1 , y 1 ) ( x 2 , y 2 ) (x_{2},y_{2}) ( x 2 , y 2 )
x 1 + y 1 = x 2 + y 2 = i + 2 x _ {1} + y _ {1} = x _ {2} + y _ {2} = i + 2 x 1 + y 1 = x 2 + y 2 = i + 2 故 i , x 1 , y 1 i, x_{1}, y_{1} i , x 1 , y 1
设 F [ i , x 1 , x 2 ] F[i, x_1, x_2] F [ i , x 1 , x 2 ] i i i x 1 x_1 x 1 x 2 x_2 x 2 y 1 = i + 2 − x 1 y_1 = i + 2 - x_1 y 1 = i + 2 − x 1 y 2 = i + 2 − x 2 y_2 = i + 2 - x_2 y 2 = i + 2 − x 2
每条路径有向右、向下两种扩展方法,故共有 2 ∗ 2 = 4 2 * 2 = 4 2 ∗ 2 = 4
如果 x 1 = x 2 x_{1} = x_{2} x 1 = x 2 y 1 + 1 = y 2 + 1 y_{1} + 1 = y_{2} + 1 y 1 + 1 = y 2 + 1
F [ i + 1 , x 1 , x 2 ] = max ( F [ i + 1 , x 1 , x 2 ] , F [ i , x 1 , x 2 ] + A [ x 1 , y 1 + 1 ] ) F [ i + 1, x _ {1}, x _ {2} ] = \max (F [ i + 1, x _ {1}, x _ {2} ], F [ i, x _ {1}, x _ {2} ] + A [ x _ {1}, y _ {1} + 1 ]) F [ i + 1 , x 1 , x 2 ] = max ( F [ i + 1 , x 1 , x 2 ] , F [ i , x 1 , x 2 ] + A [ x 1 , y 1 + 1 ]) 否则两条路径分别扩展到不同的格子,两个格子中的数都进行累加:
F [ i + 1 , x 1 , x 2 ] = max ( F [ i + 1 , x 1 , x 2 ] , F [ i , x 1 , x 2 ] + A [ x 1 , y 1 + 1 ] + A [ x 2 , y 2 + 1 ] ) F [ i + 1, x _ {1}, x _ {2} ] = \max (F [ i + 1, x _ {1}, x _ {2} ], F [ i, x _ {1}, x _ {2} ] + A [ x _ {1}, y _ {1} + 1 ] + A [ x _ {2}, y _ {2} + 1 ]) F [ i + 1 , x 1 , x 2 ] = max ( F [ i + 1 , x 1 , x 2 ] , F [ i , x 1 , x 2 ] + A [ x 1 , y 1 + 1 ] + A [ x 2 , y 2 + 1 ]) 初值为 F [ 0 , 1 , 1 ] = A [ 1 , 1 ] F[0,1,1] = \mathrm{A}[1,1] F [ 0 , 1 , 1 ] = A [ 1 , 1 ]
目标为 F [ N + M − 2 , N , N ] F[N + M - 2,N,N] F [ N + M − 2 , N , N ]
*【例题】I-country SGU167
在 N ∗ M N * M N ∗ M K K K N , M ≤ 15 , K ≤ 225 N, M \leq 15, K \leq 225 N , M ≤ 15 , K ≤ 225
任何一个凸连通块可以划分成连续的若干行,每行的左端点列号先递减、后递增,右端点列号先递增、后递减。我们可以依次考虑从 N ∗ M N * M N ∗ M
当前已经处理完的行数。
已经选出的格子数。
当前行已选格子的左端位置——为了确定下一行左端点的范围,以满足单调性。
当前行已选格子的右端位置——为了确定下一行右端点的范围,以满足单调性。
当前左侧轮廓的单调性类型——列号是该递增还是递减。
当前右侧轮廓的单调性类型——列号是该递增还是递减。
行数和格子数可以作为DP的“阶段”,每次转移到下一行,同时选出的格子数增加,在这两个维度上都符合“阶段线性增长”的特点。因此,可以设计以下的状态表示:
F [ i , j , l , r , x , y ] F[i,j,l,r,x,y] F [ i , j , l , r , x , y ] i i i j j j i i i l l l r r r x x x y y y
状态转移方程:
左边界列号递减,右边界列号递增(两个边界都处于扩张状态)。
F [ i , j , l , r , 1 , 0 ] = ∑ p = l r A [ i , p ] + { F [ i − 1 , 0 , 0 , 0 , 1 , 0 ] i f j = r − l + 1 > 0 max l ≤ p ≤ q ≤ r { F [ i − 1 , j − ( r − l + 1 ) , p , q , 1 , 0 ] } i f j > r − l + 1 > 0 \begin{array}{l} F [ i, j, l, r, 1, 0 ] \\ = \sum_ {p = l} ^ {r} A [ i, p ] + \left\{ \begin{array}{c c} F [ i - 1, 0, 0, 0, 1, 0 ] & \text {i f} j = r - l + 1 > 0 \\ \max _ {l \leq p \leq q \leq r} \left\{F [ i - 1, j - (r - l + 1), p, q, 1, 0 ] \right\} & \text {i f} j > r - l + 1 > 0 \end{array} \right. \\ \end{array} F [ i , j , l , r , 1 , 0 ] = ∑ p = l r A [ i , p ] + { F [ i − 1 , 0 , 0 , 0 , 1 , 0 ] max l ≤ p ≤ q ≤ r { F [ i − 1 , j − ( r − l + 1 ) , p , q , 1 , 0 ] } i f j = r − l + 1 > 0 i f j > r − l + 1 > 0 2.左、右边界列号都递减(左边界扩张,右边界收缩)。
F [ i , j , l , r , 1 , 1 ] = ∑ p = l r A [ i , p ] + max l ≤ p ≤ r ≤ q { max 0 ≤ y ≤ 1 { F [ i − 1 , j − ( r − l + 1 ) , p , q , 1 , y ] } } F [ i, j, l, r, 1, 1 ] = \sum_ {p = l} ^ {r} A [ i, p ] + \max _ {l \leq p \leq r \leq q} \left\{\max _ {0 \leq y \leq 1} \{F [ i - 1, j - (r - l + 1), p, q, 1, y ] \} \right\} F [ i , j , l , r , 1 , 1 ] = p = l ∑ r A [ i , p ] + l ≤ p ≤ r ≤ q max { 0 ≤ y ≤ 1 max { F [ i − 1 , j − ( r − l + 1 ) , p , q , 1 , y ]} } 3.左、右边界列号都递增(左边界收缩,右边界扩张)。
F [ i , j , l , r , 0 , 0 ] = ∑ p = l r A [ i , p ] + max p ≤ l ≤ q ≤ r { max 0 ≤ x ≤ 1 { F [ i − 1 , j − ( r − l + 1 ) , p , q , x , 0 ] } } F [ i, j, l, r, 0, 0 ] = \sum_ {p = l} ^ {r} A [ i, p ] + \max _ {p \leq l \leq q \leq r} \left\{\max _ {0 \leq x \leq 1} \{F [ i - 1, j - (r - l + 1), p, q, x, 0 ] \} \right\} F [ i , j , l , r , 0 , 0 ] = p = l ∑ r A [ i , p ] + p ≤ l ≤ q ≤ r max { 0 ≤ x ≤ 1 max { F [ i − 1 , j − ( r − l + 1 ) , p , q , x , 0 ]} } 左边界列号递增,右边界列号递减(两个边界都处于收缩状态)。
F [ i , j , l , r , 0 , 1 ] = ∑ p = l r A [ i , p ] + max p ≤ l ≤ r ≤ q { max 0 ≤ x ≤ 1 { max 0 ≤ y ≤ 1 { F [ i − 1 , j − ( r − l + 1 ) , p , q , x , y ] } } } \begin{array}{l} F [ i, j, l, r, 0, 1 ] = \sum_ {p = l} ^ {r} A [ i, p ] \\ + \max _ {p \leq l \leq r \leq q} \left\{\max _ {0 \leq x \leq 1} \left\{\max _ {0 \leq y \leq 1} \{F [ i - 1, j - (r - l + 1), p, q, x, y ] \} \right\} \right\} \\ \end{array} F [ i , j , l , r , 0 , 1 ] = ∑ p = l r A [ i , p ] + max p ≤ l ≤ r ≤ q { max 0 ≤ x ≤ 1 { max 0 ≤ y ≤ 1 { F [ i − 1 , j − ( r − l + 1 ) , p , q , x , y ]} } } 初态: F [ i , 0 , 0 , 0 , 1 , 0 ] = 0 F[i,0,0,0,1,0] = 0 F [ i , 0 , 0 , 0 , 1 , 0 ] = 0
目标: max { F [ i , K , l , r , x , y ] } \max \{F[i,K,l,r,x,y]\} max { F [ i , K , l , r , x , y ]}
时间复杂度: O ( N M 4 K ) = O ( N 2 M 5 ) O(NM^4 K) = O(N^2 M^5) O ( N M 4 K ) = O ( N 2 M 5 )
本题还要输出方案。在动态规划问题需要给出方案时,通常做法是额外使用一些与DP状态大小相同的数组记录下来每个状态的“最优解”是从何处转移而来的。最终,在DP求出最优解后,通过一次递归,沿着记录的每一步“转移来源”回到初态,即可
得到一条从初态到最优解的转移路径,也就是所求的具体方案。
【例题】Cookies 圣诞老人共有 M M M N N N i i i g [ i ] \mathrm{g}[i] g [ i ] a [ i ] a[i] a [ i ] i i i i i i g [ i ] ∗ a [ i ] \mathrm{g}[i] * a[i] g [ i ] ∗ a [ i ] N N N M M M g \mathbf{g} g 1 ≤ N ≤ 30 , N ≤ M ≤ 5000 1 \leq N \leq 30, N \leq M \leq 5000 1 ≤ N ≤ 30 , N ≤ M ≤ 5000
在这道题目中,“已经获得饼干的孩子数”和“已经发放的饼干数”显然应该作为DP的“阶段”。不过,一个孩子的怨气大小与其他孩子获得的饼干数有关,这让我们很难对状态进行划分以产生“子结构”,同时也很难计算出每个孩子的怨气值。
仔细思考可以发现,贪婪度大的孩子应该获得更多的饼干。读者用 0 × 07 0 \times 07 0 × 07 N N N
设 F [ i , j ] F[i,j] F [ i , j ] i i i j j j i i i i + 1 i + 1 i + 1
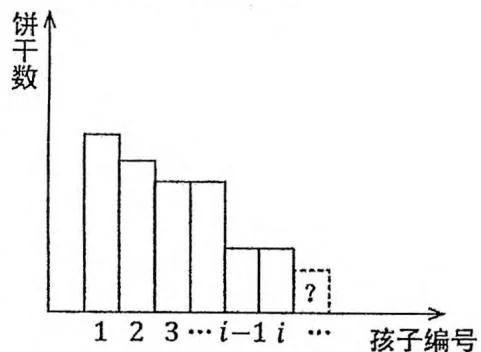
第 i + 1 i + 1 i + 1 i i i a [ i + 1 ] = i a[i + 1] = i a [ i + 1 ] = i
第 i + 1 i + 1 i + 1 i i i i i i i i i a [ i + 1 ] a[i + 1] a [ i + 1 ]
总而言之,无论哪种情况,我们都需要知道第 i i i i i i i i i
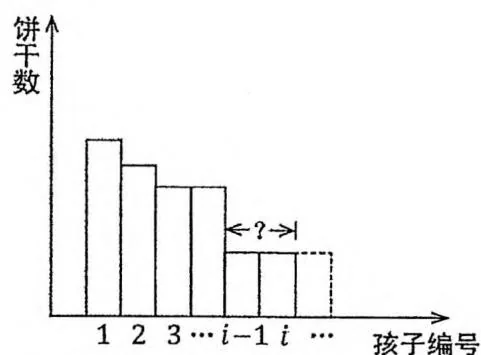
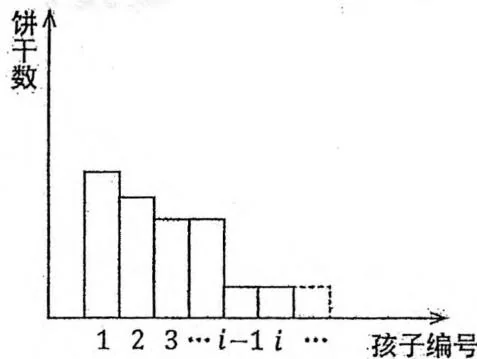
观察图中的形状,我们不妨对状态转移做一个等价转换。
若第 i i i j − i j - i j − i i i i
若第 i i i i i i
整个DP算法的状态转移方程:
F [ i , j ] = min { min 0 ≤ k < i { F [ k , j − ( i − k ) ] + k ∗ ∑ p = k + 1 i g [ p ] } F [ i, j ] = \min \left\{\min _ {0 \leq k < i} \left\{F [ k, j - (i - k) ] + k * \sum_ {p = k + 1} ^ {i} g [ p ] \right\} \right. F [ i , j ] = min ⎩ ⎨ ⎧ 0 ≤ k < i min ⎩ ⎨ ⎧ F [ k , j − ( i − k )] + k ∗ p = k + 1 ∑ i g [ p ] ⎭ ⎬ ⎫ 初态: F [ 0 , 0 ] = 0 F[0,0] = 0 F [ 0 , 0 ] = 0 F [ N , M ] F[N,M] F [ N , M ]
这道题启发我们,有时可以通过额外的算法确定DP状态的计算顺序,有时可以在状态空间中运用等效手法对状态进行缩放。在本题中,我们就利用贪心策略,在DP前对 N N N i + 1 i + 1 i + 1 i i i