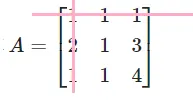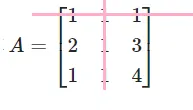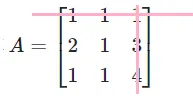16._伴随矩阵

引言

伴随矩阵是干啥用的？一句话：

伴随矩阵就是用来求逆矩阵的。

矩阵 $A$ 与其伴随矩阵 $A^*$ 之间具有如下重要关系： $A A^*=|A| E$

移项就得到

又因为

比较①②得

这样，我们就可以找到求一个矩阵的逆矩阵的统一方法。

定理 $n$ 阶方阵 $A$ 可逆的充分必要条件为 $|A| \neq 0$ ，且此时

证明：必要性．因为 $\boldsymbol{A}$ 可逆，所以存在 $\boldsymbol{A}^{-1}$ ，使得 $\boldsymbol{A} \boldsymbol{A}^{-1}= A^{-1} A=E$ ，两边取行列式，有

所以 $|\boldsymbol{A}| \neq 0$ ． 充分性．由 $A A^*=A^* A=|A| E$ ，因为 $|A| \neq 0$ ，所以 $A \frac{A^*}{|A|}= \frac{\boldsymbol{A}^*}{|\boldsymbol{A}|} \boldsymbol{A}=\boldsymbol{E}$ ，由定义知 $\boldsymbol{A}$ 可逆．又由逆矩阵唯一知 $\boldsymbol{A}^{-1}=\frac{\boldsymbol{A}^*}{|\boldsymbol{A}|}$ ．

注：$|\boldsymbol{A}| \neq 0$ ，称 $\boldsymbol{A}$ 为非奇异矩阵、非退化矩阵，非奇异、非退化与可逆是等价的概念；$|\boldsymbol{A}|=0$ ，称 $\boldsymbol{A}$ 为奇异矩阵、退化矩阵。

上述定理给出了求逆矩阵的一种方法，称为伴随矩阵法．

伴随矩阵的定义

设 $A=\left(a_{i j}\right)$ 是 $n$ 阶方阵， $A_{i j}$ 是 $|A|$ 的 $(i, j)$ 元素 $a_{i j}$ 的代数余子式则矩阵

称为矩阵 $A$ 的伴随矩阵（小心：他是代数余子式转置排列得到的矩阵）.

例求二阶方阵 $\boldsymbol{A}=\left(\begin{array}{ll}a_{11} & a_{12} \\ a_{21} & a_{22}\end{array}\right)$ 的伴随矩阵． 解：因为 $A_{11}=a_{22}, A_{12}=-a_{21}, A_{21}=-a_{12}, A_{22}=a_{11}$ ，所以

对照矩阵 $\boldsymbol{A}$ 可发现如下规律：二阶矩阵主对角线上元素交换位置，副对角线上元素反符号就得二阶方阵的伴随矩阵（此方法仅对二阶矩阵有效，一般矩阵没有此结论）。

例 求方阵 $A=\left[\begin{array}{lll}1 & 1 & 1 \\ 2 & 1 & 3 \\ 1 & 1 & 4\end{array}\right]$ 的伴随矩阵．

解：使用定义求他的伴随矩阵。 (1)划去第一行第一列，剩下的代数余子式为(代数余子式有正负号之分，详见此处)

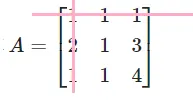
(2)划去第一行第二列，剩下的代数余子式为

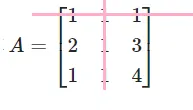
(3)划去第一行第三列，剩下的代数余子式为

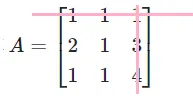
(4)划去第二行第一列，剩下的代数余子式为

(5)划去第二行第二列，剩下的代数余子式为

(6)划去第二行第三列，剩下的代数余子式为

(7)划去第三行第一列，剩下的代数余子式为

(8)划去第三行第二列，剩下的代数余子式为

(8)划去第三行第三列，剩下的代数余子式为

因此，$A$ 的伴随矩阵为

最后一步别错了，他是按列排放。

伴随矩阵的性质

伴随矩阵具有如下重要的性质

下面对①进行证明。 例 设 $\boldsymbol{A}$ 为 $n$ 阶方阵, $\boldsymbol{A}^*$ 为 $\boldsymbol{A}$ 的伴随阵, 则

证明

上式中两个矩阵乘积的第 $(i, j)$ 元素为

由行列式的代数余子式以及异乘变零定理 知道, 当 $i=j$ 时上式为 $|\boldsymbol{A}|$, 当 $i \neq j$ 时上式等于零. 因此

同理可证

从性质① 可以得到，$\boldsymbol{A}^{-1}=\frac{1}{|\boldsymbol{A}|} \boldsymbol{A}^*$ 这给我我们一个求逆矩阵的方法，先求出他的伴随矩阵，再求出他的行列式，然后做一个除法即可。

例设 $n$ 阶矩阵 $\boldsymbol{A}$ 的伴随阵为 $\boldsymbol{A}^*$, 证明: （1）若 $|\boldsymbol{A}|=0$ ，则 $\left|\boldsymbol{A}^*\right|=0$ ； （2）$\left|\boldsymbol{A}^*\right|=|\boldsymbol{A}|^{n-1}$.

证（1）因

当 $|\boldsymbol{A}|=0$ 时, 上式成为 $\boldsymbol{A}^* \boldsymbol{A}=\boldsymbol{O}$ 。 要证 $\left|\boldsymbol{A}^*\right|=0$ ，用反证法：设 $\left|\boldsymbol{A}^*\right| \neq 0$ ，由矩阵可逆的充要条件知， $\boldsymbol{A}^*$ 是可逆矩阵，用 $\left(\boldsymbol{A}^*\right)^{-1}$ 左乘上式等号两边，得 $\boldsymbol{A}=\boldsymbol{O}$ 。于是推得 $\boldsymbol{A}$ 的所有 $n-1$ 阶子式，亦即 $\boldsymbol{A}^*$ 的所有元素均为零。这导致 $\boldsymbol{A}^*=\boldsymbol{O}$ 。此与 $\boldsymbol{A}^*$ 为可逆矩阵矛盾。这一矛盾说明，当 $|\boldsymbol{A}|=0$ 时， $\left|\boldsymbol{A}^*\right|=0$ 。 （2）分两种情形: 情形1: $|\boldsymbol{A}|=0$ 。由 (1), $\left|\boldsymbol{A}^*\right|=0=|\boldsymbol{A}|^{n-1}$ ，结论成立； 情形 $2:|\boldsymbol{A}| \neq 0$ 。在（2.5）式的两边取行列式，得

于是

例若 $4 \times 4$ 阶矩阵 $A$ 的行列式为 $|A|=3, A^*$ 是 $A$ 的伴随矩阵，则 $\left|A^*\right|=$

解：利用上面这个结论，

可以得到 $|A^*|=|A|^{n-1}$ ,可以直接求的 27

这是一个非常小的知识点，据观察90%考试会考到这个小技巧，请务必要记住。

补充小知识

在上面证明里，涉及到一个小知识：设$A$是一个矩阵，$|A|$是矩阵对应的行列式，当计算 $||A||$时，他的结果是 $|A|^n$, 这是因为 在 $||A||$ 里层的$|A|$是一个“数”，当把一个数往行列式外提取出来时，需要是该数的$n$次方，详见 二阶行列式 的性质3

使用伴随矩阵求逆矩阵

伴随矩阵主要作用就是求逆矩阵，第一步求出卖个元素的代数余子式，第二部按位置排好各个元素,具体请看下面例子

例求

的伴随矩阵

解：

把上面求的代数余子式排列成矩阵形式，于是$A$的伴随矩阵为

$A$得逆矩阵

从解题过程可以看到，伴随矩阵计算量非常大，但是计算机喜欢。

伴随矩阵的作用

从上面求解逆矩阵的过程看，伴随矩阵计算量太大，要求一个矩阵的逆矩阵，要分别对每个元素求他的代数余子式，然后还要排列放起来，因此，考试时，基本上不会考用伴随矩阵求逆矩阵。但是，伴随矩阵思路简单，适合计算机进行处理，而且，伴随矩阵性质多，因此，考试时，他多作为小题考察学生。

例讨论下面矩阵 $A$ 在何时可逆，并求出其逆矩阵。这里 $A=\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)$ 。

解：因为 $|A|=\left|\begin{array}{ll}a & b \\ c & d\end{array}\right|=a d-b c$ ，所以当且仅当 $a d-b c \neq 0$时，原矩阵可逆，且其逆矩阵为：

例 设矩阵 $A$ 的伴随矩阵

且 $A B A^{-1}=B A^{-1}+3 I$ ．求矩阵 $B$ ． 解 因 $A A^*=|A| I$ ，两边取行列式得 $|A|\left|A^*\right|=|A|^n .(n=$ 4），因已知 $A$ 可逆，故 $|A| \neq 0$ ．于是 $\left|A^*\right|=|A|^3$ ．而 $\left|A^*\right|=8$ ．所以 $|A|=2$ ．

由已知 $A B A^{-1}=B A^{-1}+3 I$ 得 $A B A^{-1}-B A^{-1}=3 I$ ．故 $(A-I) B A^{-1}=3 I$ ，即 $(A-I) B=3 A$ 。两边左乘 $A^{-1}$有 $A^{-1}(A-I) B=3 I$ ．得 $\left(I-A^{-1}\right) B=3 I$ ． 即 $\left(I-\frac{A^*}{|A|}\right) B=3 I,|A|=2$ 代人，即得 $\left(2 I-A^*\right) B=6 I$ ． 又 $2 I-A^*$ 为可逆矩阵．于是

代入已知数据：由

有

因此得