15._矩阵的转置

矩阵的转置

定义： 设矩阵 A=(123456)A=\left(\begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6\end{array}\right) 这是一个3×23 \times 2 得矩阵，把矩阵 AA 的行、列互换得到的矩阵称为矩阵 AA 的转置矩阵，互换后矩阵变成2×32 \times 3型,记为 ATA^{\mathrm{T}} ，即

AT=(142536).A^{\mathrm{T}}=\left(\begin{array}{ll} 1 & 4 \\ 2 & 5 \\ 3 & 6 \\ \end{array}\right) .

矩阵转置的性质

矩阵的转置满足下面的运算规律 (这里 kk 为常数， AA 与 BB 为同型矩阵)： (1)(AT)T=A\left(\boldsymbol{A}^{\mathrm{T}}\right)^{\mathrm{T}}=\boldsymbol{A} (2)(A+B)T=AT+BT(\boldsymbol{A}+\boldsymbol{B})^{\mathrm{T}}=\boldsymbol{A}^{\mathrm{T}}+\boldsymbol{B}^{\mathrm{T}} (3) (AB)T=BTAT(\boldsymbol{A} \boldsymbol{B})^{\mathrm{T}}=\boldsymbol{B}^{\mathrm{T}} \boldsymbol{A}^{\mathrm{T}} (4) (kA)T=kAT(k \boldsymbol{A})^{\mathrm{T}}=k \boldsymbol{A}^{\mathrm{T}}

请注意第三条性质可以推广 (ABC)T=CTBTAT(\boldsymbol{A} \boldsymbol{B}\boldsymbol{C)}^{\mathrm{T}}=\boldsymbol{C}^{\mathrm{T}} \boldsymbol{B}^{\mathrm{T}} \boldsymbol{A}^{\mathrm{T}}

矩阵转置的计算

例设矩阵 A=(2−13111),B=(1−102−11)\boldsymbol{A}=\left(\begin{array}{ccc}2 & -1 & 3 \\ 1 & 1 & 1\end{array}\right), B=\left(\begin{array}{cc}1 & -1 \\ 0 & 2 \\ -1 & 1\end{array}\right), 求 (AB)T(\boldsymbol{A} \boldsymbol{B})^{\mathrm{T}}. 解法一：

AB=(2−13111)(1−102−11)=(−1−102), 所以 (AB)T=(−10−12). \boldsymbol{A} \boldsymbol{B}=\left(\begin{array}{ccc} 2 & -1 & 3 \\ 1 & 1 & 1 \end{array}\right)\left(\begin{array}{cc} 1 & -1 \\ 0 & 2 \\ -1 & 1 \end{array}\right)=\left(\begin{array}{cc} -1 & -1 \\ 0 & 2 \end{array}\right) \text {, 所以 }(\boldsymbol{A B})^{\mathrm{T}}=\left(\begin{array}{ll} -1 & 0 \\ -1 & 2 \end{array}\right) \text {. }

解法二：

(AB)T=BTAT=(10−1−121)(21−1131)=(−10−12).(\boldsymbol{A} \boldsymbol{B})^{\mathrm{T}}=\boldsymbol{B}^{\mathrm{T}} \boldsymbol{A}^{\mathrm{T}}=\left(\begin{array}{ccc} 1 & 0 & -1 \\ -1 & 2 & 1 \end{array}\right)\left(\begin{array}{cc} 2 & 1 \\ -1 & 1 \\ 3 & 1 \end{array}\right)=\left(\begin{array}{cc} -1 & 0 \\ -1 & 2 \end{array}\right) .

转置的作用1-对称矩阵

定义2 nn 阶方阵 AA 如果满足 AT=AA^{\mathrm{T}}=A ，则称 AA 为对称矩阵，如果满足 AT=−AA^{\mathrm{T}}=-A ，则称 AA 为反对称矩阵. 由定义可知， 1 如果 nn 阶方阵 A=(aij)\boldsymbol{A}=\left(a_{i j}\right) 是对称矩阵，则 aij=aji(i≠j;i,j=1,2,⋯ ,n)a_{i j}=a_{j i}(i \neq j ; i, j=1,2, \cdots, n). 如果 nn 阶方阵 A=(aij)A=\left(a_{i j}\right) 是反对称矩阵， 则 aij=−aji(i≠j;i,j=1,2,⋯ ,n)a_{i j}=-a_{j i}(i \neq j ; i, j=1,2, \cdots, n) ，且 aii=0(i=1,2,⋯ ,n)a_{i i}=0(i=1,2, \cdots, n).

例 设矩阵 A\boldsymbol{A} 是 m×nm \times n 矩阵，证明: ATA\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A} 和 AAT\boldsymbol{A A ^ { \mathrm { T } }} 都是对称矩阵. 证明 因为

(ATA)T=AT(AT)T=ATA,(AAT)T=(AT)TAT=AAT,\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}\right)^{\mathrm{T}}=\boldsymbol{A}^{\mathrm{T}}\left(\boldsymbol{A}^{\mathrm{T}}\right)^{\mathrm{T}}=\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}, \quad\left(\boldsymbol{A} \boldsymbol{A}^{\mathrm{T}}\right)^{\mathrm{T}}=\left(\boldsymbol{A}^{\mathrm{T}}\right)^{\mathrm{T}} \boldsymbol{A}^{\mathrm{T}}=\boldsymbol{A} \boldsymbol{A}^{\mathrm{T}},

所以 ATAA^{\mathrm{T}} A 和 AATA A^{\mathrm{T}} 都是对称矩阵.

注意：在矩阵证明题里，要证明一个矩阵是对称矩阵，通常使用 AT=AA^T=A 这个性质

转置的作用2-解方程

(1) 传统的我们都使用AX=BAX=B的方程，然后直接使用逆矩阵解方程，详见 逆矩阵解方程组 , 假设有方程 XA=BXA=B, 若矩阵 AA 可逆，则有

(XA)A−1=BA−1⇒X(AA−1)=BA−1⇒X=BA−1.(\mathrm{X} A) A^{-1}=B A^{-1} \Rightarrow X\left(A A^{-1}\right)=B A^{-1} \Rightarrow X=B A^{-1} .

例 解方程

X(10−20−21−2−15)=(−11012−1)\boldsymbol{X}\left(\begin{array}{ccc} 1 & 0 & -2 \\ 0 & -2 & 1 \\ -2 & -1 & 5 \end{array}\right)=\left(\begin{array}{ccc} -1 & 1 & 0 \\ 1 & 2 & -1 \end{array}\right)

分析：虽然我们可以求出A−1A^{-1},然后再左乘以BB，但是要计算A−1A^{-1}就要进行一次初等变换，毫无疑问计算量很大，我们希望尽可能一次性计算出来。此时我们矩阵转置的思维。

对于方程 XA=BX A=B ，可以先用初等行变换求解方程 ATXT=BT A^{\mathrm{T}} X^{\mathrm{T}}=B^{\mathrm{T}}，再转置求出X X

解：

(AT∣BT)=(10−2−110−2−112−2150−1)\left(\boldsymbol{A}^{\mathrm{T}} \mid \boldsymbol{B}^{\mathrm{T}}\right)=\left(\begin{array}{ccc|cc} 1 & 0 & -2 & -1 & 1 \\ 0 & -2 & -1 & 1 & 2 \\ -2 & 1 & 5 & 0 & -1 \end{array}\right)
∼(10−2−110−2−112011−21)\sim \left(\begin{array}{ccc|cc} 1 & 0 & -2 & -1 & 1 \\ 0 & -2 & -1 & 1 & 2 \\ 0 & 1 & 1 & -2 & 1 \end{array}\right)
∼(10−2−11011−21001−34)\sim \left(\begin{array}{ccc|cc} 1 & 0 & -2 & -1 & 1 \\ 0 & 1 & 1 & -2 & 1 \\ 0 & 0 & 1 & -3 & 4 \end{array}\right)
∼(100−790101−3001−34)\sim \left(\begin{array}{ccc|cc} 1 & 0 & 0 & -7 & 9 \\ 0 & 1 & 0 & 1 & -3 \\ 0 & 0 & 1 & -3 & 4 \end{array}\right)

所以 XT=(−791−3−34)\boldsymbol{X}^{\mathrm{T}}=\left(\begin{array}{cc}-7 & 9 \\ 1 & -3 \\ -3 & 4\end{array}\right) \quad 从而 X=(−71−39−34)\boldsymbol{X}=\left(\begin{array}{ccc}-7 & 1 & -3 \\ 9 & -3 & 4\end{array}\right)

(2)假设有一个矩阵方程 AXB=CA X B=C 变量在中间，若矩阵 A、BA 、 B 可逆均可逆，通过左乘A−1A^{-1},右乘B−1B^{-1} 则有

A−1(AXB)B−1=A−1CB−1⇒(A−1A)X(BB−1)=A−1CB−1⇒X=A−1CB−1.A^{-1}(A X B) B^{-1}=A^{-1} C B^{-1} \Rightarrow\left(A^{-1} A\right) X\left(B B^{-1}\right)=A^{-1} C B^{-1} \Rightarrow X=A^{-1} C B^{-1} .

例 解方程

(11−1−2)X(−11001−110−2)=(1−10−101)\left(\begin{array}{cc} 1 & 1 \\ -1 & -2 \end{array}\right) \boldsymbol{X}\left(\begin{array}{ccc} -1 & 1 & 0 \\ 0 & 1 & -1 \\ 1 & 0 & -2 \end{array}\right)=\left(\begin{array}{ccc} 1 & -1 & 0 \\ -1 & 0 & 1 \end{array}\right)

解：

此题是 AXB=C\boldsymbol{A} \boldsymbol{X B}=\boldsymbol{C} 类型的方程．令 XB=Y\boldsymbol{X B}=\boldsymbol{Y} ，先求解方程 AY=C\boldsymbol{A Y}=\boldsymbol{C} ，然后求解方程 BTXT=YT\boldsymbol{B}^{\mathrm{T}} \boldsymbol{X}^{\mathrm{T}}=\boldsymbol{Y}^{\mathrm{T}} ，最后转置求出 X\boldsymbol{X} 。

(A∣C)=(111−10−1−2−101)→r2+r1(111−100−10−11)→(−1)r2r1+r2(101−210101−1)(\boldsymbol{A} \mid \boldsymbol{C})=\left(\begin{array}{cc|ccc} 1 & 1 & 1 & -1 & 0 \\ -1 & -2 & -1 & 0 & 1 \end{array}\right) \xrightarrow{r_2+r_1}\left(\begin{array}{cc|ccc} 1 & 1 & 1 & -1 & 0 \\ 0 & -1 & 0 & -1 & 1 \end{array}\right) \xrightarrow[(-1) r_2]{r_1+r_2}\left(\begin{array}{cc|ccc} 1 & 0 & 1 & -2 & 1 \\ 0 & 1 & 0 & 1 & -1 \end{array}\right)

于是得 Y=(1−2101−1)\boldsymbol{Y}=\left(\begin{array}{ccc}1 & -2 & 1 \\ 0 & 1 & -1\end{array}\right) ．再由

(BT∣YT)=(−10110110−210−1−21−1)→r2+r1(−10110011−110−1−21−1)→(−1)hr3+r2(−10110011−1100100)→r2+(−1)rnr2(−1)r5(−1)rn(100−10010−1100100)\left(\boldsymbol{B}^{\mathrm{T}} \mid \boldsymbol{Y}^{\mathrm{T}}\right)=\left(\begin{array}{ccc|cc} -1 & 0 & 1 & 1 & 0 \\ 1 & 1 & 0 & -2 & 1 \\ 0 & -1 & -2 & 1 & -1 \end{array}\right) \xrightarrow{r_2+r_1}\left(\begin{array}{ccc|cc} -1 & 0 & 1 & 1 & 0 \\ 0 & 1 & 1 & -1 & 1 \\ 0 & -1 & -2 & 1 & -1 \end{array}\right) \xrightarrow[(-1) h]{r_3+r_2}\left(\begin{array}{ccc|cc} -1 & 0 & 1 & 1 & 0 \\ 0 & 1 & 1 & -1 & 1 \\ 0 & 0 & 1 & 0 & 0 \end{array}\right) \xrightarrow[r_2+(-1) r_n]{\substack{r_2(-1) r_5 \\ (-1) r_n}}\left(\begin{array}{ccc|cc} 1 & 0 & 0 & -1 & 0 \\ 0 & 1 & 0 & -1 & 1 \\ 0 & 0 & 1 & 0 & 0 \end{array}\right)

可知 XT=(−10−1100)\boldsymbol{X}^{\mathrm{T}}=\left(\begin{array}{cc}-1 & 0 \\ -1 & 1 \\ 0 & 0\end{array}\right) ，从而 X=(−1−10010)\boldsymbol{X}=\left(\begin{array}{ccc}-1 & -1 & 0 \\ 0 & 1 & 0\end{array}\right) ．

矩阵对平面和空间的旋转变换

在矩阵乘法的本质论里 讨论了矩阵乘法的意义。 平面和空间中的旋转变换是很常见的, 我们在前面的例子里也多次谈到旋转矩阵, 又比如工程中我们要模拟飞机在空中的前后、左右和上下的旋转动作等。因此, 弄清旋转矩阵是很有意思的。下面我们就详细讨论这个问题。

平面上点的旋转变换

如图所示, 平面上任意一点 P(x,y)P(x, y) 对应的向量 oP→\overrightarrow{o P} (与原点 oo 相连接得到), 以逆时针方向绕原点在平面上旋转 θ\theta 角, 得到向量 OP′→\overrightarrow{O P^{\prime}}, 即点 P(x,y)P(x, y) 在平面上以逆时针方向绕原点旋转 θ\theta 角, 变化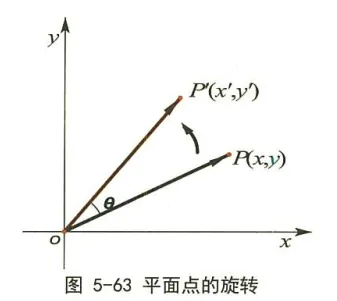到点 P′(x′,y′)P^{\prime}\left(x^{\prime}, y^{\prime}\right) 。 图片 如果我们记这个变换为 Γ\boldsymbol{\Gamma}, 那么有 oP′→=ΓOP→\overrightarrow{o P^{\prime}}=\boldsymbol{\Gamma} \overrightarrow{O P} 。实际上这个点的旋转变换 Γ\boldsymbol{\Gamma} 就是前面我们介绍的旋转矩阵 (cos⁡θ−sin⁡θsin⁡θcos⁡θ)\left(\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta\end{array}\right), 即点（或向量）的旋转变换为

(x′y′)=[cos⁡θ−sin⁡θsin⁡θcos⁡θ](xy)\left(\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right)=\left[\begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]\left(\begin{array}{l} x \\ y \end{array}\right)

具体推导也可以参加高中解析几何教程，即 http://kb.kmath.cn/kbase/detail.aspx?id=1339

平面上坐标的旋转变换

如果将坐标系 {xoy}\{x o y\} 也以逆时针方向绕原点旋转 θ\theta 角, 会得到新的坐标系 {x′oy′}\left\{x^{\prime} o y^{\prime}\right\}, 如图 5-64 所示。旧坐标轴上的基本单位向量 i\boldsymbol{i} 和 j\boldsymbol{j} 变为新坐标轴上的基本单位向量 i′\boldsymbol{i}^{\prime} 和 j′\boldsymbol{j}^{\prime}, 即 i′=Γi\boldsymbol{i}^{\prime}=\boldsymbol{\Gamma} \boldsymbol{i}, j′=Γj\boldsymbol{j}^{\prime}=\boldsymbol{\Gamma} \boldsymbol{j} 。实际上, 此时的旋转效果是最终对坐标系 {xoy}\{x o y\} 和向量 o⃗P⃗\vec{o} \vec{P} 一起做了旋转 θ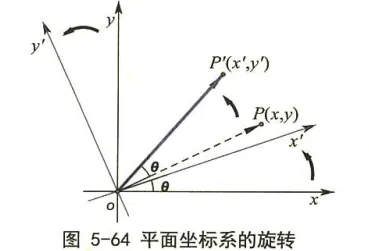\theta 角的操作。 图片 考察基本单位向量的变化, 容易检验 i′\boldsymbol{i}^{\prime} 关于旧坐标轴的坐标为 (cos⁡θ,sin⁡θ)(\cos \theta, \sin \theta), 即

i′=icos⁡θ+jsin⁡θ\boldsymbol{i}^{\prime}=\boldsymbol{i} \cos \theta+\boldsymbol{j} \sin \theta

同理, 有

j′=icos⁡(θ+π2)+jsin⁡(θ+π2)=−isin⁡θ+jcos⁡θ\begin{aligned} \boldsymbol{j}^{\prime} & =\boldsymbol{i} \cos \left(\theta+\frac{\pi}{2}\right)+\boldsymbol{j} \sin \left(\theta+\frac{\pi}{2}\right) \\ & =-\boldsymbol{i} \sin \theta+\boldsymbol{j} \cos \theta \end{aligned}

即

{i′=icos⁡θ+jsin⁡θj′=−isin⁡θ+jcos⁡θ 或 (i′j′)=[cos⁡θsin⁡θ−sin⁡θcos⁡θ](ij)\left\{\begin{array}{l} \boldsymbol{i}^{\prime}=\boldsymbol{i} \cos \theta+\boldsymbol{j} \sin \theta \\ \boldsymbol{j}^{\prime}=-\boldsymbol{i} \sin \theta+\boldsymbol{j} \cos \theta \end{array} \quad \text { 或 } \quad\left(\begin{array}{l} \boldsymbol{i}^{\prime} \\ \boldsymbol{j}^{\prime} \end{array}\right)=\left[\begin{array}{cc} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right]\left(\begin{array}{l} \boldsymbol{i} \\ \boldsymbol{j} \end{array}\right)\right.

式中, [cos⁡θsin⁡θ−sin⁡θcos⁡θ]\left[\begin{array}{rr}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta\end{array}\right] 称为坐标系 (单位向量) 旋转变换矩阵, 记为 T\boldsymbol{T} 。 我们看到点的旋转矩阵和坐标系的同样旋转的旋转矩阵 T\boldsymbol{T} 不同, 容易验证, 它们互为转置矩阵。

矩阵转置的通俗解释就是：想象一下地球和太阳的关系，如果我们假设地球是静止的，那么就是太阳围着地球转。如果我们假设太阳是静止的，那么就是地球围着太阳转，所以，在图形和坐标旋转里，一种是图形不动，坐标旋转。 一种是坐标不动，图像旋转。而矩阵转置告诉我们，两者本质是一样的。

另外, 也可以验证它们互为逆矩阵。因为坐标系的坐标轴 (只是坐标轴, 不包括平面上的点或者向量) 作逆时针旋转 θ\theta 角就相当于平面上的点或者向量 (不包括坐标轴) 作顺时针旋转 θ\theta角, 如图 所示。 图片

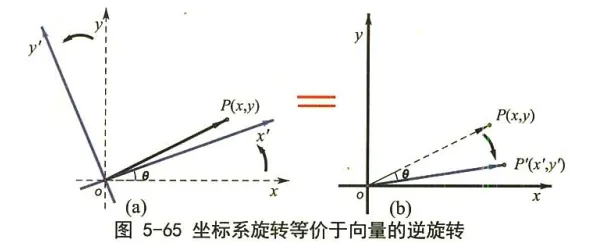
坐标系的旋转的变换公式可以通过作图得到, 这个图也可以看做这个变换矩阵的几何解释。设原坐标系是 {xoy}\{x o y\}, 这个坐标系以原点 oo 为固定点进行逆时针旋转 θ\theta 角, 得到新的直角坐标系 {x′oy},P\left\{x^{\prime} o y\right\}, P 点保持不动, 则旋转的图像如图 5-66 (a) 所示。 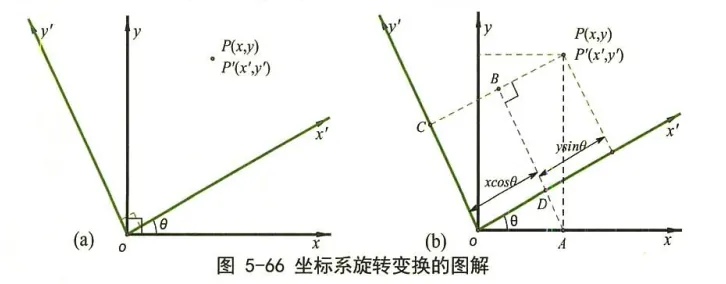图片 为分析 PP 点在两个坐标系中的坐标值之间的变换关系, 从 PP 点分别作四个坐标轴的垂线,然后作 ABA B 垂直于 PCP C 线段, 得到图 5-66 (b) 所示的图形, 则 PP 点在 {x′oy′}\left\{x^{\prime} o y^{\prime}\right\} 坐标系下的值分别是

{x′=PB+BCy′=AB−AD\left\{\begin{array}{l} x^{\prime}=P B+B C \\ y^{\prime}=A B-A D \end{array}\right.

把式中线段 PBP B 等的长度分别用三角式子替换, 即可得到前面的旋转变换的公式。

转置矩阵的几何意义

本节我们看到, 在二维的旋转变换中, 空间里元素 (如向量或点) 的旋转矩阵和对应的坐标系 (坐标轴) 旋转矩阵既是逆矩阵也是转置矩阵。 这有助于我们理解转置矩阵在几何上的意义, 可以简单地认为：空间和空间元素之间的相对旋转运动的几何描述是转置矩阵的几何意义。这样容易记忆矩阵转置的性质，例如 (AT)T=A\left(\boldsymbol{A}^{\mathrm{T}}\right)^{\mathrm{T}}=\boldsymbol{A} 当一个图形旋转180度，在旋转180度，就回到了图形本身。

矩阵转置的作用

矩阵转置核心用法就一个： 如果(AT)=A\left(\boldsymbol{A}^{\mathrm{T}}\right)=\boldsymbol{A} 则这个矩阵是对称矩阵。 如果这个矩阵是对称矩阵，则(AT)=A\left(\boldsymbol{A}^{\mathrm{T}}\right)=\boldsymbol{A}

后面在学习二次型时，会用到对称矩阵，而在考试时，经常出题证明矩阵A是对称矩阵。如何证明A是对称矩阵，通常就是证明矩阵A的转置等于矩阵A，这是固定套路。

上一章14._正交矩阵
下一章16._伴随矩阵