在 矩阵乘法的视图 里会介绍更多乘法的视角。但是核心掌握下面几个就可以了
矩阵的乘法
设矩阵 A=(aij) 是一个 m×p 矩阵, 矩阵 B=(bij) 是一个 p×n 矩阵, 定义矩阵 A 与 B 的乘积是
一个 m×n 矩阵 C=(cij) ,其中矩阵 C=(cij) 的第 i 行第 j 列元素 cij 是由矩阵 A 的第 i 行元素a11,a2,⋯,ap 与矩阵 B 的第 j 列相应元素 b1j,b2j,⋯,bB 乘积之和,即
cij=k=1∑paikbkj=ai1b1j+ai2b2j+⋯+aipbpj. 定义有点绕口,直接看例子。
矩阵乘法举例
例 计算
(142536)×791181012= 解:我们使用行向量视角,第一个矩阵是2×3矩阵,第二个矩阵是3×2矩阵,所以结果将是一个2×2的矩阵。
c11=1∗7+2∗9+3∗11=58
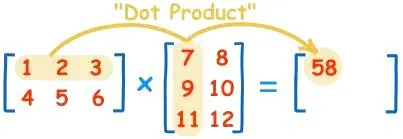
同理,
c12=1∗8+2∗10+3∗12=64
c21=4∗7+5∗9+6∗11=139
c22=4∗8+5∗10+6∗12=154
所以,结果是
(142536)×791181012=(5813964154) 上面结算结果是:用第一个矩阵的行和第二个矩阵的列相乘,然后得到的结果作为结果矩阵里的元素。这种以行为主的内积运算(也称点积)虽然很容易方便(计算机)处理,但是却不利于我们人脑的理解。
我们应该拥有更高维度更清晰的视角看待矩阵——以列为主,即列向量
例 计算
223347[x1x2]=2x1+3x22x1+4x23x1+7x2 仔细看一下列2,你发现了什么了吗?是的,乘积的结果矩阵 相当于用x1,x2 分别乘以矩阵A的前两列,再相加。
列视角理解矩阵乘法
本课程叫做《线性代数》,核心包含了“线性”和“代数”两层含义,在 引言了介绍了 线性代数 四字的意义。
只有以列为视角,才能把线性组合关联起来。
以列为主的视角将矩阵乘法视为对矩阵的列向量进行线性组合。所谓线性组合,即线性+组合,线性是指向量乘以一个标量,沿着向量的方向缩放,方向不变;组合是把多个向量加起来。列视角是线性代数非常核心的基础概念,基础并不是说它简单,而是说它像地基一样重要,在学习任何线代知识前,应该先要打好的地基。
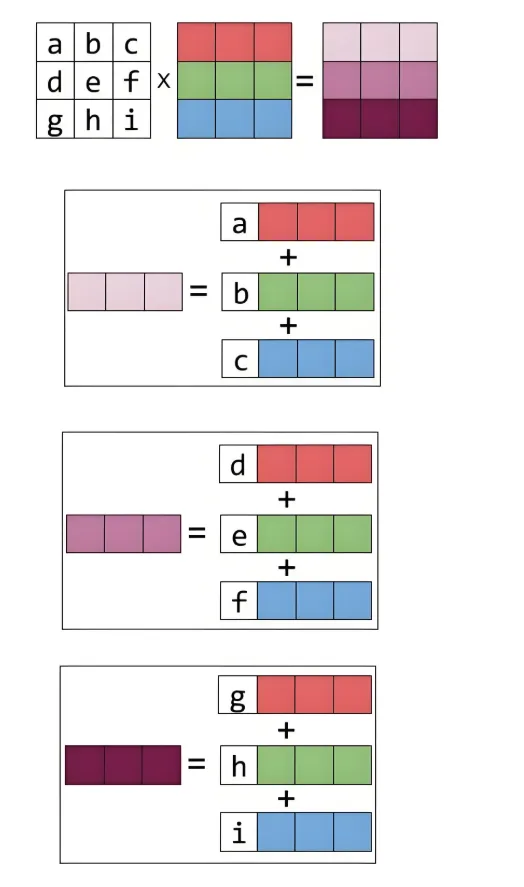
参考下图
红绿蓝三种颜色乘以矩阵 A=(a,b,c)T,得到的结果是红色乘以a,绿色乘以b,蓝色乘以c,然后得到紫色
这里体现了两层含义:线性,即红绿蓝分别被a,b,c作用,彼此不被干扰。 组合,就是把最终结果相加。
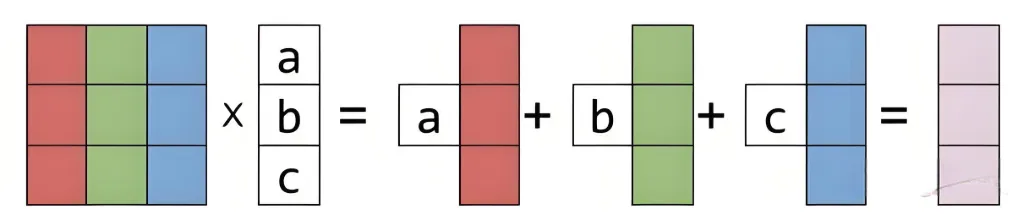
推广
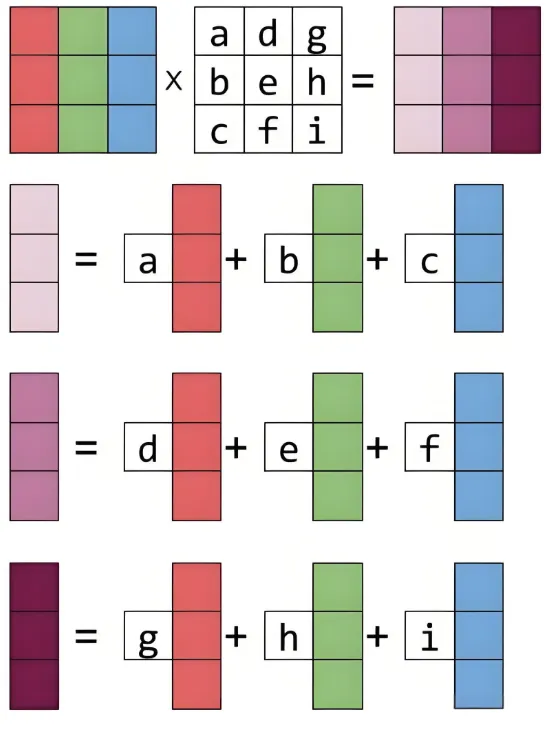
现在把上面的结果推广,把矩阵A推广为多列,
为了方便理解,我们从结果看过程
可以看到,最后的结果就是前面线性的叠加。
A=abceefghi (a,b,c) 作用颜色的结果的第一列,(d,e,f)作用颜色的结果作为第二列,(g,h,i)作用颜色的结果作为第三列。 换句话说,每一列的结果只与对应的列有关,而和别的列无关
这就像,下课了,嘈杂的教师里,你能立刻分别出小明和小军的声音,虽然教室里各种同学声音杂乱无章,但是对你而言,“小明”的声音和小军的声音好想彼此不干扰一样。
理解了上面的思想,再来看例1的乘法。
例 计算
(142536)×791181012=? 解:我们使用列向量视角,就可以把矩阵转换为
(142536)×7911000+(142536)×00081012 (5813900)+(0064154) =(5813964154) 注意:正如上面所说,使用列视角方便人脑的理解,但是计算量反而可能比行视角大,所以行视角多用于计算机处理中。
列视角下的方程组
设有方程
⎩⎨⎧a11x1+a12x2+⋯+a1nxn=b1a21x1+a22x2+⋯+a2nxn=b2⋯⋯⋯am1x1+am2x2+⋯+amnxn=bm 则方程可以写成
Ax=a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮annx1x2⋮xn=x1a11a21⋮an1+x2a12a2c⋮an2+⋯+xna1na2n⋮ann=b 仅从长相上看,矩阵方程 Ax=β初中学习的代数方程 ax=b 几乎张一模一样。
矩阵乘法的性质
例求矩阵 A=(32−1210) 与 B=112−11101−1 的乘积 AB.
解 因为矩阵 A 是 2×3 矩阵,矩阵 B 是 3×3 矩阵, A 的列数等于 B 的行数,所以矩阵 A 与 B 可 以相乘,乘积 AB 是一个 2×3 矩阵.
AB=(32−1210)112−11101−1=(3×1+(−1)×1+1×22×1+2×1+0×23×(−1)+(−1)×1+1×12×(−1)+2×1+0×13×0+(−1)×1+1×(−1)2×0+2×1+0×(−1))=(44−30−22) 例求矩阵 A=(−121−2) 与 B=(2−61−3) 的乘积 AB 及 BA.
解 AB=(−121−2)(2−61−3)=(−816−48);
BA=(2−61−3)(−121−2)=(0000). 注意:
(1) 矩阵乘法不满足交换律,即在一般情况下, AB=BA.
(2) 尽管矩阵 A 与 B 满足 AB=O ,但是得不出 A=O 或 B=O 的结论.
矩阵乘法满足的运算规律
结合律:
(AB)C=A(BC) ;
矩阵乘法对矩阵加法的分配律:
A(B+C)=AB+AC,(A+B)C=AC+BC ;
数乘
(kA)B=A(kB)=k(AB);
单位矩阵
EmAm×n=Am×nEn=Am×n;
矩阵乘法
Om×sAs×n=Om×n;Am×sOs×n=Om×n.
方阵的幂
定义方阵的方幂如下: Ak=k↑AA⋯A (这里 k 为正整数),
并且规定:对非零方阵 A ,有 A0=E.
方阵的方幂满足以下运算规律 (这里 k,l 均为非负整数) :
AkAl=Ak+l;(Ak)l=Akl. 由于矩阵乘法不满足交换律,一般来讲 (AB)k=AkBk,(A+B)2=A2+2AB+B2.
只有当 A 与 B 可交换(即 AB=BA) 时,公式
(AB)k=AkBk,(A+B)2=A2+2AB+B2,(A+B)(A−B)=A2−B2 等才成立.
例设矩阵 A=000100010, 求 A2 和 A3.
A2A3=000100010000100010=000000100,=A2A=000000100000100010=000000000. 行视角理解矩阵乘法(不方便人脑的理解)
矩阵左乘行向量,向量对矩阵的行进行线性组合,结果向量位于矩阵的行空间
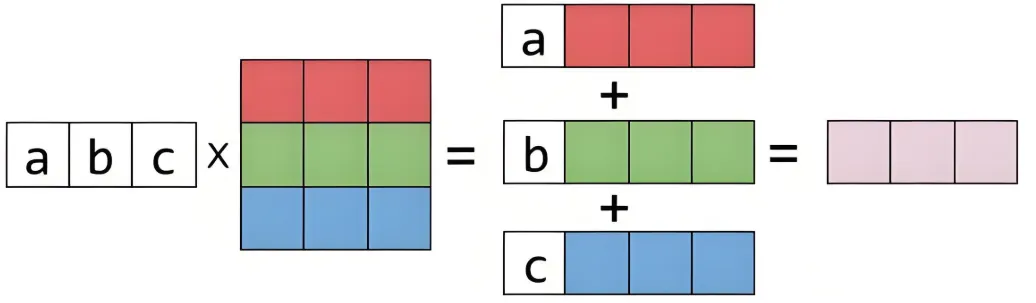
左侧的向量可以延展为一个由若干行所组成的矩阵,每一行乘以右边的矩阵,得到结果矩阵中的一行。
矩阵的高纬推广
在计算机学习里,会遇到多维数组,为了方便理解多维数组的内涵,下面简单介绍高纬度矩阵。
1维矩阵
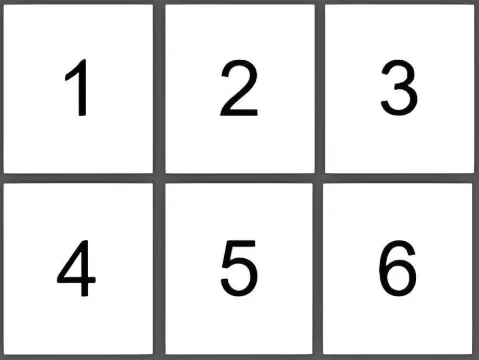
shape=[1,2,3,4]
 {width=200px}
{width=200px}
2维矩阵
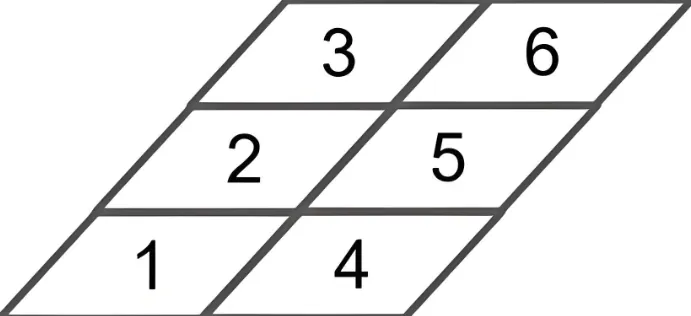
shape=[[1. 2. 3.]
[4. 5. 6.]]
看维度的小技巧:想知道一个矩阵的维度是几维的,只需要看开头有几个“[”,有1个即为1维,上面的两个就是两维,后面举到的三维和四维的例子,分别是有三个“[”、四个“[”的。
上面这两维可视化长这样:
 {width=200px}
{width=200px}
为了方便后续解释三维和四维,我们把它旋转一个小角度,如下
 {width=300px}
{width=300px}
3维矩阵
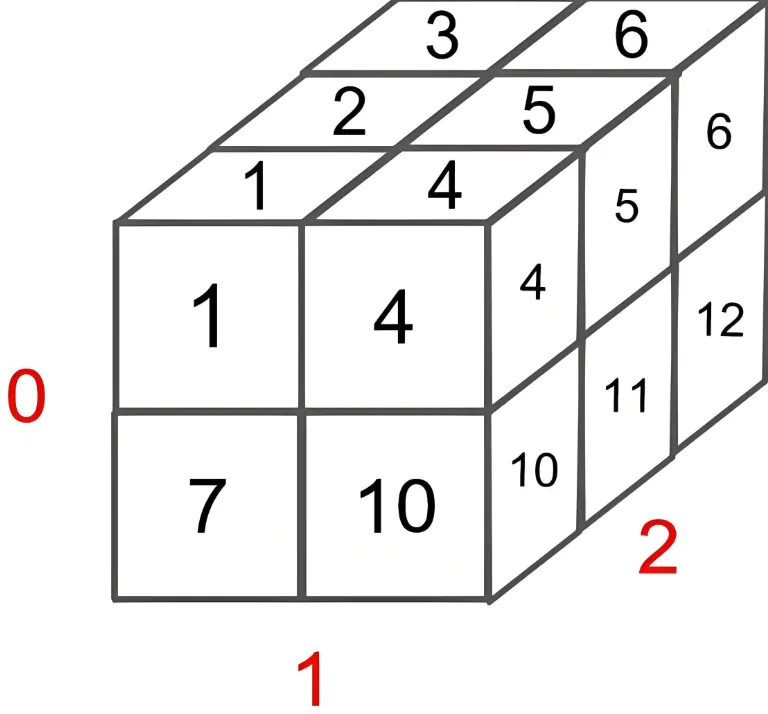
shape=[[[ 1. 2. 3.]
[ 4. 5. 6.]]
[[ 7. 8. 9.]
[10. 11. 12.]]]
可以看到这是一个三维空间,是2×2×3 维度
 {width=350px}
{width=350px}
如果切片则显示数据如下
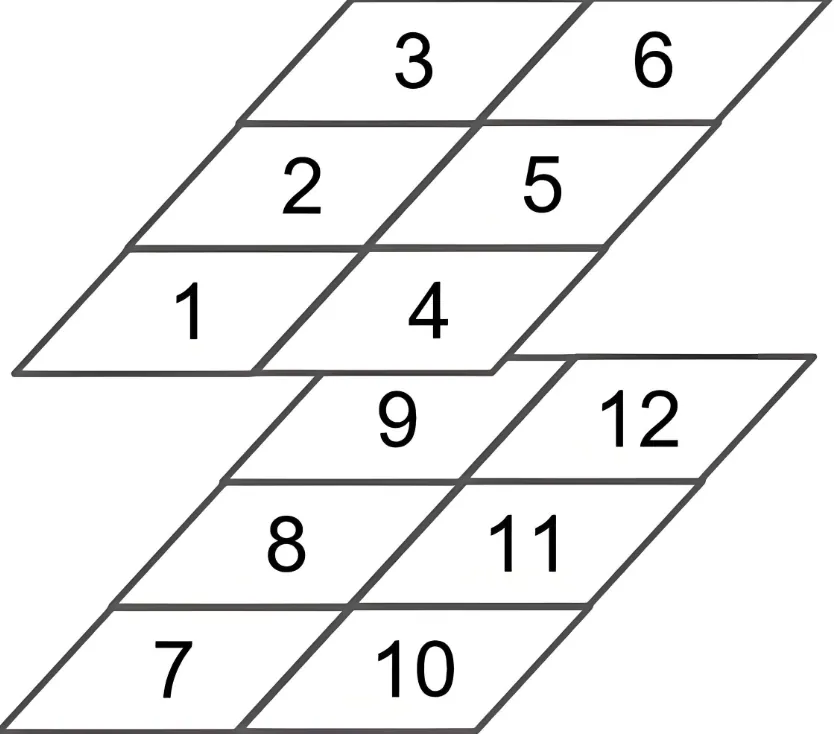 {width=350px}
{width=350px}
结论:shape=[2,2,3]的三维矩阵,可以视为2个shape=[2,3]的二维矩阵堆叠在一起!!最后两维才是有数据的矩阵,前面的维度只是矩阵的排列而已!
注意上图中红色的0,1,2,表示的是输出的三个维度,在可视化中的位置。
总结怎么画三维:
先根据shape画出一个三维,shape=[2,2,3]分别对应着可视化中红色的0,1,2中小格子的个数
填充两维,在可视化中分别是1,2这两个维度上,把数据填充上,也就是上半部分的[[ 1. 2. 3.] [ 4. 5. 6.]]
填充剩余部分的[[ 7. 8. 9.] [10. 11. 12.]],并堆叠在一起形成三维。
四维
shape=[[[[ 1. 2. 3.]
[ 4. 5. 6.]]
[[ 7. 8. 9.]
[10. 11. 12.]]]
[[[13. 14. 15.]
[16. 17. 18.]]
[[19. 20. 21.]
[22. 23. 24.]]]]
结论:shape=[2,2,2,3]的四维矩阵,可以视为2个shape=[2,2,3]的三维矩阵堆叠在一起!!然后三维的最后是用二维的堆叠组成的!!第一个2表示的是batchsize!!最后两维才是有数据的矩阵,前面的维度只是矩阵的排列而已!
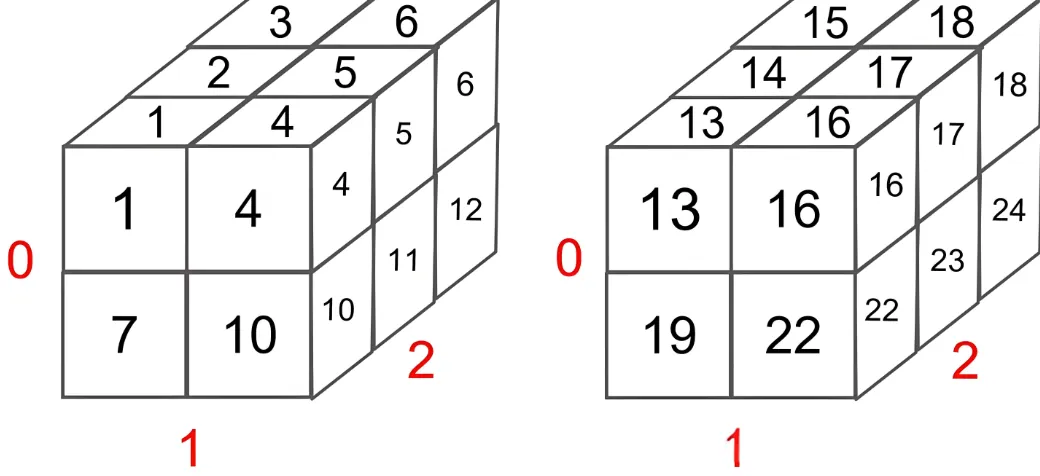 {width=600px}
{width=600px}
注:本文综合了知乎矩阵乘法列空间、 多维矩阵向量运算 等文章改编。

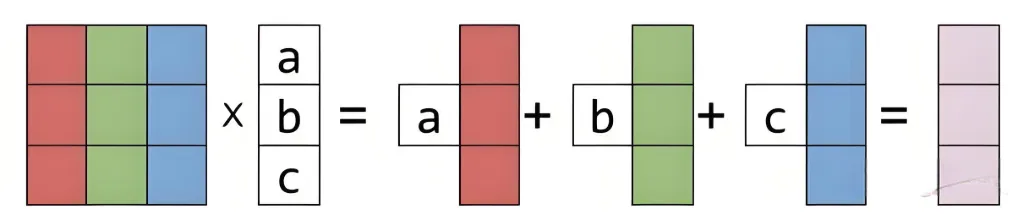



 {width=200px}
{width=200px} {width=200px}
{width=200px} {width=300px}
{width=300px} {width=350px}
{width=350px} {width=350px}
{width=350px} {width=600px}
{width=600px}