列视角理解矩阵乘法
本课程叫做《线性代数》,核心包含了“线性”和“代数”两层含义,在 引言了介绍了 线性代数 四字的意义。
只有以列为视角,才能把线性组合关联起来。
以列为主的视角将矩阵乘法视为对矩阵的列向量进行线性组合。所谓线性组合,即线性+组合,线性是指向量乘以一个标量,沿着向量的方向缩放,方向不变;组合是把多个向量加起来(向量加法使用平行四边形法则,可以直接坐标相加)。列视角是最重要的视角。
参考下图
红绿蓝三种颜色乘以矩阵 A=abc,得到的结果是红色乘以a,绿色乘以b,蓝色乘以c,然后得到紫色
这里体现了两层含义:线性,即红绿蓝分别被a,b,c作用,彼此不被干扰。 组合,就是把最终结果相加。
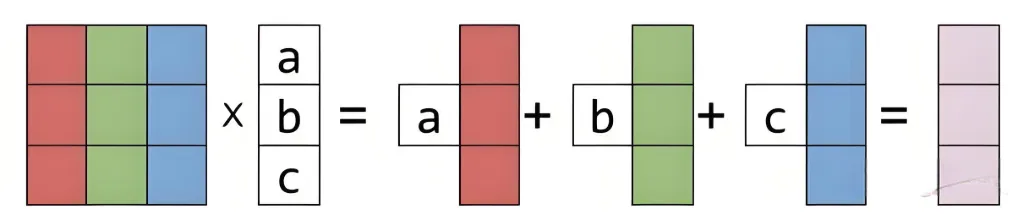
比如下面这个矩阵乘法
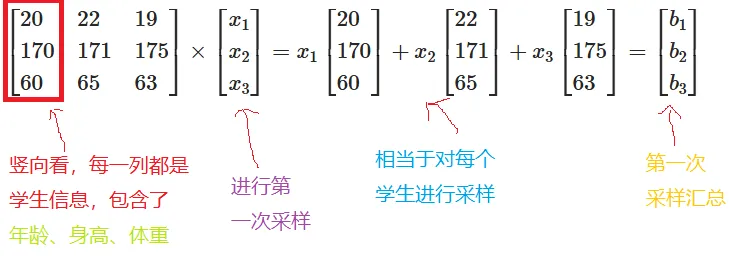
201706022171651917563×x1x2x3=x12017060+x22217165+x31917563=b1b2b3 上面的矩阵乘法可以理解为:有一组学生,每一列都包含了学生的基本信息:年龄、身高和体重。现在对每个学生进行采样,采样次数分别是x1,x2,x3次,最终形成了第一批采样报告 B=b1b2b3
多次采样
假设有一天又进行了第二次采样,如下
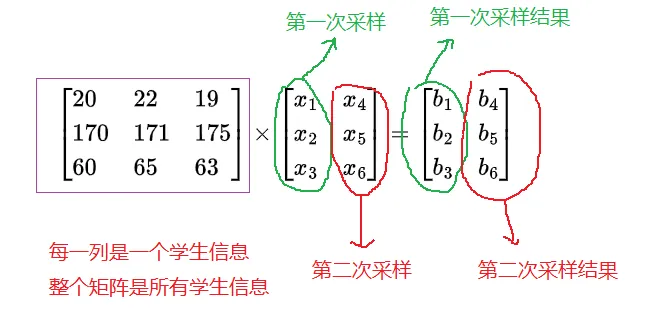
201706022171651917563×x1x2x3x4x5x6=b1b2b3b4b5b6 参考下图可以看到,每一列采样数据和采样结果彼此互相对应,如果把上面看成方程,我们发现变量还是竖着写舒服,因为能跟右边的值一一对应起来。进一步的,可以发现这个方程其实是2个方程组,含有6个等式。
如果采样次数是第三次、第四次、第n次呢?不用担心,直接把汇总结果矩阵继续案列放置即可。所以按列理解矩阵乘法,是最常用的思考方式。
推广
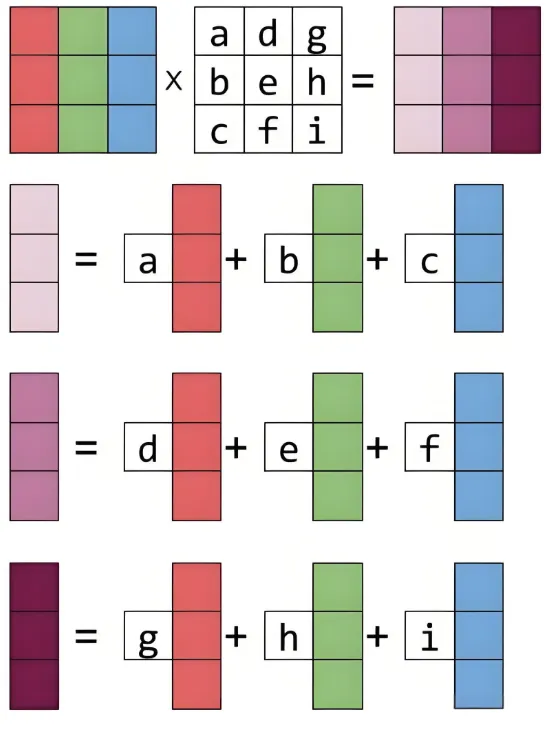
现在把上面的结果推广,把矩阵A推广为多列,为了方便理解,我们从结果看过程 可以看到,最后的结果就是前面线性的叠加。
理解了上面的思想,再来看矩阵乘法。
例 计算
(142536)×791181012=? 解:我们使用列向量视角,就可以把矩阵转换为
(142536)×7911000+(142536)×00081012 (5813900)+(0064154) =(5813964154) 注意:正如上面所说,使用列视角方便人脑的理解,但是计算量反而可能比行视角大,所以行视角多用于计算机处理中。
列视角下的方程组
设有方程
⎩⎨⎧a11x1+a12x2+⋯+a1nxn=b1a21x1+a22x2+⋯+a2nxn=b2⋯⋯⋯an1x1+an2x2+⋯+annxn=bn 则方程可以写成
Ax=a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮annx1x2⋮xn=x1a11a21⋮an1+x2a12a22⋮an2+⋯+xna1na2n⋮ann=b **仅从长相上看,矩阵方程 Ax=β 和初中学习的代数方程 ax=b 长相几乎张一模一样, 都是左边是数,中间是x右边是结果 **,
上面这种把方程转换为矩阵的写法要能倒过来理解,即给了一个矩阵方程,能理解他的传统方程的写法。
向量空间的视角
现在我们把矩阵以列视角,从向量空间来观察他,考察下面一个矩阵乘法
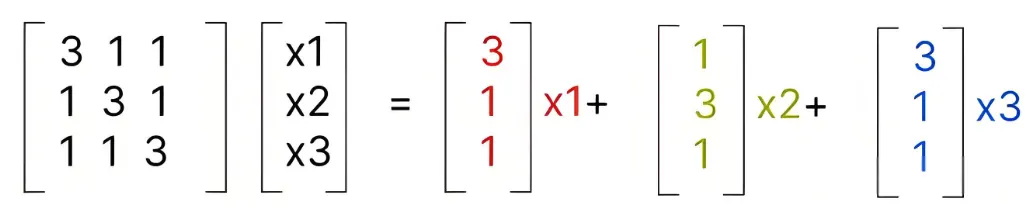
如果把矩阵的列当做三维空间的x,y,z 坐标轴,那么这3个向量将张成三维空间,根据平行四边形法则,空间的任何一个向量,在这个三维空间里都有自己的坐标值(x1,x2,x3), 参考下图
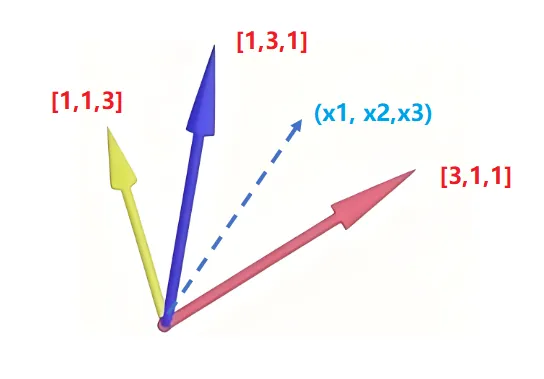 {width=300px}
{width=300px}
因此, 在这种思维模型下,AX=B中的AX可以看成一个向量在A空间里的坐标值是X,那么B呢?
我们说一个向量,要测量他的大小和方向,得有一个“尺度”,最常用的是笛卡尔坐标系,即e1=(1,0,0),e2=(0,1,0),e3=(0,0,1),其实B隐含这E单位矩阵。即
AX=EB,即
311131113123=10001000181012 你可以这么理解:
A空间里看到的一个向量,他的坐标值是 123 如果我换一个标准的视角E去看他,他的坐标值是 81012 两个值相等表示向量还是那个向量,只是观察角度不一样了。
如果把矩阵视为拍照,你给小猪猪可以正面拍,侧面拍,上面拍,下面拍,猪还是那头猪,但是拍摄的角度不一样,得到的照片并不一样。在这些拍照里,有一个视角是最好的:就是正面拍照,因为不失真,这个正面其实就是我们说的单位矩阵E。
同样,如下面的矩阵
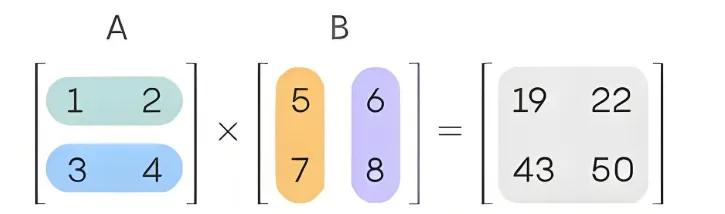 可以看成在
可以看成在
[1324] 里看到的2个向量 [57] 和 [68] 换到笛卡尔坐标系下看,变成了 [1943] 和 [2250]
矩阵右乘
如果我们把上面矩阵固定不变,用给猪猪拍照做类比,向量右乘一个矩阵,可以看到相当于“改变了坐标系,进而改变了观察的视角”,对比见下表
| 场景 | 左乘 | 右乘 |
|---|
| 坐标变换 | 将点从原坐标系变换到新坐标系 | 将坐标系本身进行变换 |
| 图形学 | 旋转、缩放物体(物体不动,坐标系不变) | 改变观察视角(坐标系旋转,物体不变) |
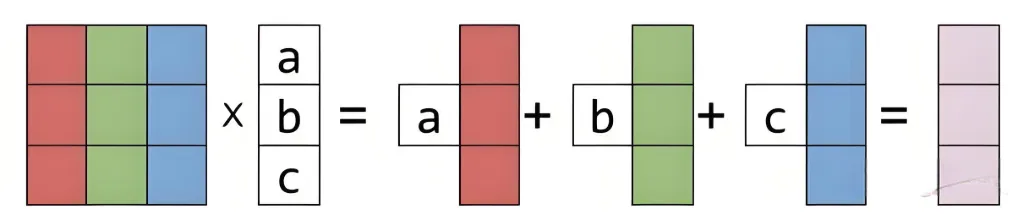




 {width=300px}
{width=300px} 可以看成在
可以看成在