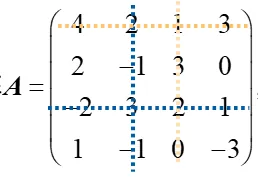9._余子式与代数余子式 - 线性代数

余子式与代数余子式

一般来说，低阶行列式的计算比高阶行列式的计算要简单，于是，我们自然的考虑是用低阶行列式来表达高阶行列式。

定义

余子式：设 $|A|$ 是一个 $n$ 阶行列式，划去的第 $i$ 行及第 $j$ 列，剩下的 $(n-1)^2$ 个元素按照原来的顺序组成了一个 $n-1$ 行列式，这个行列式称为 $|A|$ 的第 $(i, j)$ 元素的余子式，记为 $M_{i j}$ 。

M_{i j}=\left|\begin{array}{cccccc} a_{11} & \cdots & a_{1, j-1} & a_{1, j+1} & \cdots & a_{1 n} \\ \vdots & & \vdots & \vdots & & \vdots \\ a_{i-1,1} & \cdots & a_{i-1, j-1} & a_{i-1, j+1} & \cdots & a_{i-1, n} \\ a_{i+1,1} & \cdots & a_{i+1, j-1} & a_{i+1, j+1} & \cdots & a_{i+1, n} \\ \vdots & & \vdots & \vdots & & \vdots \\ a_{n 1} & \cdots & a_{n, j-1} & a_{n, j+1} & \cdots & a_{n n} \end{array}\right| .

你看到这个定义，你想到了什么？是降阶！！通过循环递归的方式，比如把5阶行列式转换成4阶行列式，循环用上面的定义，把4阶行列式转换为3阶行列式，把3阶行列式转换为2阶行列式，直到最后转换为1阶行列式。这是我们处理高阶行列式最原始的想法，因此提出了余子式的概念。

我们注意到三阶行列式的值是用二阶行列式来定义的，而二阶行列式又可以由一阶来定义，这是一个递归的想法，因此 $n$ 阶行列式的值可以用 $n-1$ 阶行列式来定义. 即我们可以用归纳法来定义上述行列式 $|\boldsymbol{A}|$ 的值.

根据上面定义，当 $n=1$ 时, 上式的值定义为 $|\boldsymbol{A}|=a_{11}$ . 现假定对 $n-1$ 阶行列式已经定义了它们的值, 则对任意的 $i, j, M_{i j}$ 的值已经定义, 定义 $n$ 阶行列式 $|\boldsymbol{A}|$ 的值为

|\boldsymbol{A}|=a_{11} M_{11}-a_{21} M_{21}+\cdots+(-1)^{n+1} a_{n 1} M_{n 1} ...... (1.7.2)

对于任一自然数 $n,(1.7.2)$ 式给出了一个计算 $n$ 阶行列式的方法: 将 $n$ 阶行列式化为 $n-1$ 阶行列式，再化 $n-1$ 阶行列式为 $n-2$ 阶， $\cdots$ ，最后便可求出 $|\boldsymbol{A}|$ 的值. 上式又称为行列式 $|\boldsymbol{A}|$ 按第一列展开的展开式.

为了使 $(1.7.2)$ 式的形状更好些, 我们引进代数余子式的概念.

代数余子式

设 $|A|$ 是一个 $n$ 阶行列式， $M_{i j}$ 是 $|A|$ 的第 $(i, j)$ 元素的余子式，定义 $|A|$ 的第 $(i, j)$ 元素的代数余子式为: $A_{ij}=(-1)^{i+j} M_{i j}$

从定义可以看出，代数余子式比余子式多了一个正负号（为什么多了一个正负号？因为在行列式案列展开时，每一项会多一个正负号）。

用代数余子式表示 $(1.7.2)$ 式可写为如下形状:

|\boldsymbol{A}|=a_{11} A_{11}+a_{21} A_{21}+\cdots+a_{n 1} A_{n 1} ......(1.7.3)

这样便于记忆。

一个常见的问题是：为什么代数余子式比余子式多了一个正负符号？仔细比较(1.7.2)和(1.7.3)，可以发现余子式 $M_{ij}$ 和代数余子式 $A_{ij}$ 之间正好差了一个 $(-1)^{i+j}$ 符号，所以为了“平衡”两者关系，才加了一个正负号。换句话说，如果M和A差了一个2被，那可能定义代数余子式为余子式的二倍。

举例

设矩阵 $A$ 为4阶行列式，如下图，

$图片$

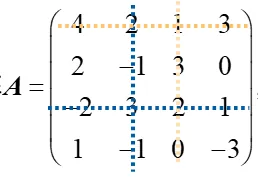
①按照第三行第二列展开（蓝色虚线），则 $|\boldsymbol{A}|$ 的 $(3,2)$ 元素的余子式和代数余子式分别为

M_{32}=\left|\begin{array}{ccc} 4 & 1 & 3 \\ 2 & 3 & 0 \\ 1 & 0 & -3 \end{array}\right|, \quad A_{32}=(-1)^{3+2} M_{32}=-M_{32}

②按照第一行和第三列展开（橙色虚线），则 $|\boldsymbol{A}|$ 的 $(1,3)$ 元素的余子式和代数余子式分别为

M_{13}=\left|\begin{array}{ccc} 2 & -1 & 0 \\ -2 & 3 & 1 \\ 1 & -1 & -3 \end{array}\right| \quad, \quad A_{13}=(-1)^{1+3} M_{13}=M_{13}

要注意余子式和代数余子式的区别，再求余子式的时候，只需要注意划去某行或者某列，在求行列式即可；但是在求代数余子式的时候，要注意正负号的区别，这个是一个易错点，请大家注意.

代数余子式的性质

行列式 $D=\left|a_{i j}\right|_n$ 等于它的任意一行的元素与其代数余子式的乘积之和

\sum_{k=1}^n a_{k i} A_{k j}= \begin{cases}D, & \text { 当 } i=j, \\ 0, & \text { 当 } i \neq j\end{cases}

我们会在下一节证明这个定理，有兴趣的同学可以自己先想想怎么证明：

我们已经知道三阶行列式的计算：

\left|\begin{array}{lll} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right|=a_{11}\left|\begin{array}{ll} a_{22} & a_{23} \\ a_{32} & a_{33} \end{array}\right|-a_{12}\left|\begin{array}{ll} a_{21} & a_{23} \\ a_{31} & a_{33} \end{array}\right|+a_{13}\left|\begin{array}{ll} a_{21} & a_{22} \\ a_{31} & a_{32} \end{array}\right| .

仔细看，他其实就是按照第一行展开的。

推论1

一行元素与另外一行元素的代数余子式乘积之和为0 即 $a_{i 1} A_{j 1}+a_{i 2} A_{j 2}+\cdots+a_{i n} A_{j n}=\sum_{k=1}^n a_{i k} A_{j k}=0(i \neq j),$

例题

计算

D=\left|\begin{array}{rrrrr} 5 & 3 & -1 & 2 & 0 \\ 1 & 7 & 2 & 5 & 2 \\ 0 & -2 & 3 & 1 & 0 \\ 0 & -4 & -1 & 4 & 0 \\ 0 & 2 & 3 & 5 & 0 \end{array}\right|

解：仔细观察这个行列式最后一列包含的0最多，因此，我们使用最后一列进行展开。

\begin{aligned} D=\left|\begin{array}{rrrrr} 5 & 3 & -1 & 2 & 0 \\ 1 & 7 & 2 & 5 & 2 \\ 0 & -2 & 3 & 1 & 0 \\ 0 & -4 & -1 & 4 & 0 \\ 0 & 2 & 3 & 5 & 0 \end{array}\right| & =(-1)^{2+5} 2\left|\begin{array}{rrrr} 5 & 3 & -1 & 2 \\ 0 & -2 & 3 & 1 \\ 0 & -4 & -1 & 4 \\ 0 & 2 & 3 & 5 \end{array}\right|=-2 \times 5\left|\begin{array}{rrr} -2 & 3 & 1 \\ -4 & -1 & 4 \\ 2 & 3 & 5 \end{array}\right| \\ & =-10\left|\begin{array}{rrr} -2 & 3 & 1 \\ 0 & -7 & 2 \\ 0 & 6 & 6 \end{array}\right|=(-10) \times(-2)\left|\begin{array}{rr} -7 & 2 \\ 6 & 6 \end{array}\right| \\ & =20(-42-12)=-1080 . \end{aligned}

例题

逆用代数余子式求值。

传统的，都是给出矩阵，然后利用代数余子式求矩阵的值，但是考试时，不会考这种题，因为简单大家都会，他会要求你逆用代数余子式，即给一个代数余子式，你要想办法凑起来他的矩阵，这样题目要求你求代数余子式就转换为求矩阵。

例已知行列式

D_5=\left|\begin{array}{lllll} 1 & 2 & 3 & 4 & 5 \\ 2 & 2 & 2 & 1 & 1 \\ 3 & 1 & 2 & 4 & 5 \\ 1 & 1 & 1 & 2 & 2 \\ 4 & 3 & 1 & 5 & 0 \end{array}\right|=27

计算 $A_{41}+A_{42}+A_{43}+A_{44}+A_{45}$ 以及 $A_{41}$ .

解:（1）我们要逆用代数余子式的概念，这里第四行为 $(1,1,1,2,2)$ 我们希望他变成 $(1,1,1,1,1)$

根据行列式的性质6：若行列式中某行 (列) 元素均为两项之和, 则行列式可表示为两个行列式之和。所以，第四行可以拆开乘3个行列式 $(1,1,1,1,1)$ 之和因此， $A_{41}+A_{42}+A_{43}+A_{44}+A_{45}$ $=\left|\begin{array}{lllll}1 & 2 & 3 & 4 & 5 \\ 2 & 2 & 2 & 1 & 1 \\ 3 & 1 & 2 & 4 & 5 \\ 1 & 1 & 1 & 1 & 1 \\ 4 & 3 & 1 & 5 & 0\end{array}\right|=9$ .

A_{41}=(-1)^{4+1}\left|\begin{array}{cccc} 2 & 3 & 4 & 5 \\ 2 & 2 & 1 & 1 \\ 1 & 2 & 4 & 5 \\ 3 & 1 & 5 & 0 \end{array}\right|=-3

仔细观察本题，我们在计算 $A_{41}+A_{42}+A_{43}+A_{44}+A_{45}$ 时，我们把原有行列式的第4行全部换为 1 ，那么这个 1 到底是为什么? 因为再确定代数余子式时，是由除去 $a_{i j}$ 所在的行与列的其他元素决定的，跟 $a_{i j}$ 所在位置的具体数值无关，比如要求让你求 $a A_{41}+b A_{42}+c A_{43}+d A_{44}+e A_{45}$ ， (其中 $a, b, c, d, e$ 为任意数字)那么该怎么办呢，只需要我们把第四行依次换为 $a, b, c, d, e$ 在求行列式即可。

例设

D=\left|\begin{array}{ccccc} 1 & 1 & 1 & \cdots & 1 \\ 0 & 1 & 1 & \cdots & 1 \\ 0 & 0 & 1 & \cdots & 1 \\ \vdots & \vdots & \vdots & & \vdots \\ 0 & 0 & 0 & \cdots & 1 \end{array}\right|

求 $D$ 的所有元素的代数余子式之和. 解: 显然有行列式 $D$ 的最后一列都是1，利用行列式展开公式可得:

A_{1 k}+A_{2 k}+\cdots+A_{n k}=\left\{\begin{array}{c} 0, k \neq n \\ |D|=1, k=n \end{array}\right.

所以可得:

\sum_{i=1}^n \sum_{y=1}^n A_{i j}=0+0+\cdots+0+1=1

例 设

D=\left|\begin{array}{rrrr} 3 & -5 & 2 & 1 \\ 1 & 1 & 0 & -5 \\ -1 & 3 & 1 & 3 \\ 2 & -4 & -1 & -3 \end{array}\right|

$D$ 的 $(i, j)$ 元的余子式和代数余子式依次记作 $M_{i j}$ 和 $A_{i j}$ , 求

A_{11}+A_{12}+A_{13}+A_{14} \text { 及 } M_{11}+M_{21}+M_{31}+M_{41} \text {. }

解按代数余子式可知 $A_{11}+A_{12}+A_{13}+A_{14}$ 等于用 $1,1,1,1$ 代替 $D$ 的第 1 行所得的行列式, 即

\begin{aligned} &\begin{aligned} & A_{11}+A_{12}+A_{13}+A_{14} \\ = & \left|\begin{array}{rrrr} 1 & 1 & 1 & 1 \\ 1 & 1 & 0 & -5 \\ -1 & 3 & 1 & 3 \\ 2 & -4 & -1 & -3 \end{array}\right| \xlongequal[r_3-r_1]{r_4+r_3}\left|\begin{array}{rrrr} 1 & 1 & 1 & 1 \\ 1 & 1 & 0 & -5 \\ -2 & 2 & 0 & 2 \\ 1 & -1 & 0 & 0 \end{array}\right| \\ = & \left|\begin{array}{rrr} 1 & 1 & -5 \\ -2 & 2 & 2 \\ 1 & -1 & 0 \end{array}\right| \xlongequal{c_2+c_1}\left|\begin{array}{rrr} 1 & 2 & -5 \\ -2 & 0 & 2 \\ 1 & 0 & 0 \end{array}\right|=\left|\begin{array}{rr} 2 & -5 \\ 0 & 2 \end{array}\right|=4 \end{aligned}\\ &\text { 按（10）式可知 }\\ &M_{11}+M_{21}+M_{31}+M_{41}=A_{11}-A_{21}+A_{31}-A_{41} \end{aligned}

按第一列，

\begin{aligned} & =\left|\begin{array}{rrrr} 1 & -5 & 2 & 1 \\ -1 & 1 & 0 & -5 \\ 1 & 3 & 1 & 3 \\ -1 & -4 & -1 & -3 \end{array}\right| \xlongequal{r_4+r_3}\left|\begin{array}{rrrr} 1 & -5 & 2 & 1 \\ -1 & 1 & 0 & -5 \\ 1 & 3 & 1 & 3 \\ 0 & -1 & 0 & 0 \end{array}\right| \\ & =(-1)\left|\begin{array}{rrr} 1 & 2 & 1 \\ -1 & 0 & -5 \\ 1 & 1 & 3 \end{array}\right| \xlongequal{r_1-2 r_3}-\left|\begin{array}{rrr} -1 & 0 & -5 \\ -1 & 0 & -5 \\ 1 & 1 & 3 \end{array}\right|=0 \end{aligned}

注意：上面是一个基本技巧，考研时，常用

例已知 $|\boldsymbol{A}|=\left|\begin{array}{rrrr}1 & 0 & 1 & 2 \\ -1 & 1 & 0 & 3 \\ 1 & 1 & 1 & 0 \\ -1 & 2 & 5 & 4\end{array}\right|$ ．（1）求 $A_{12}-A_{22}+A_{32}-A_{42}$ ；（2）求 $A_{41}+A_{42}+A_{43}+A_{44}$ ，这里 $A_{i j}$ 是 $|\boldsymbol{A}|$ 中元素 $a_{i j}$ 的代数余子式

解．（1）令 $D=\left|\begin{array}{rrrr}1 & 1 & 1 & 2 \\ -1 & -1 & 0 & 3 \\ 1 & 1 & 1 & 0 \\ -1 & -1 & 5 & 4\end{array}\right|$ ．由已知条件易见， $A_{12}-A_{22}+A_{32}-A_{42}=D$ ．经计算，得 $D=0$ ，所以 $A_{12}-A_{22}+A_{32}-A_{42}=0$ ．（2）令 $D=\left|\begin{array}{rrrr}1 & 0 & 1 & 2 \\ -1 & 1 & 0 & 3 \\ 1 & 1 & 1 & 0 \\ 1 & 1 & 1 & 1\end{array}\right|$ ．由已知条件易见， $A_{41}+A_{42}+A_{43}+A_{44}=D$ 。经计算，得 $D=-1$ ，所以 $A_{41}+A_{42}+A_{43}+A_{44}=-1$ ．

行列式展开的几何意义

在介绍三阶行列式时，我们说他的值为(a,b,c)向量张成向量空间的体积。例如有下面一个行列式

D=\left|\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 &1 \\ \end{array}\right|

他的3行向量分别是 $\vec{a}=(1,0,0)=\vec{x}$ $\vec{b}=(0,1,0)=\vec{y}$ $\vec{c}=(0,0,1)=\vec{z}$

$图片$

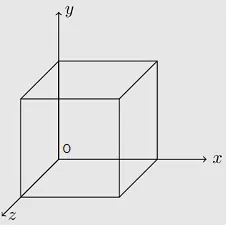
很容易看出他的体积为 $x*y*z=1$ ，因此上述行列式的值 $D=1$

但是，利用余子式计算，就相当于以计算3次，即

以xoz为底，以oy为高计算一次
以xoy为底，以oz为高计算一次
以yoz为底，以ox为高计算一次

这样体积计算了3次，通过引入代数余子式，增加正负号，可以抵消一个体积，进而得出正确的提交。

那么，又如何理解一行元素与另外一行元素的代数余子式乘积之和为0 呢？仍以上图为例，一行元素和另外一行代数余子式的乘积，相当于以xoz为底，以 $ox$ 为高，求其体积，而ox本身在xoz平面式，自然体积为0.

注意上面仅是为了方便理解和记忆，不做真实推理依据