数域上的线性方程组(或向量空间)的意义 在使用高斯消元法解方程组时, 大家有没有注意一个有意思的细节: 在整个解的过程中,只进行加减乘除四则运算, 没有涉及开方运算, 更没有涉及解二次以至更高次方程的计算。由此看来, 我们可以得到以下的推论:
假设线性方程组的增广矩阵的元素全部是有理数 (意思方程组的系数和常数项全部是有理数), 那么加、减、乘、除的消元计算结果只能是有理数。如果我们定义方程组的基础解系中的任意数为有理数, 则方程组的解集也是有理数, 从而我们可以完全在有理数的范围内讨论线性方程组。
类似地, 我们也可以把对方程组的讨论限制在实数域, 因为加、减、乘、除不会出现虚数。
对方程组的讨论可以限定在某个数域, 数域的定义是:
一个集合 K K K K K K K K K Q \mathbf{Q} Q R \mathbf{R} R C \mathbf{C} C { a + b i \{a+b \mathrm{i} { a + b i a , b a, b a , b } \} } a + b i a+b \mathrm{i} a + b i
全体的整数集合不是数域, 因为对除法不封闭, 两整数相除会出现分数。
有了数域的概念后, 前面的讨论都可以限制在某一个数域上了。如以数域 K K K K K K K K K
如果以数域 K K K n n n K K K K K K K K K n n n R \mathbf{R} R n n n R n \mathbf{R}^n R n C \mathbf{C} C n n n C n \mathbf{C}^n C n ( ∈ ) (\in) ( ∈ )
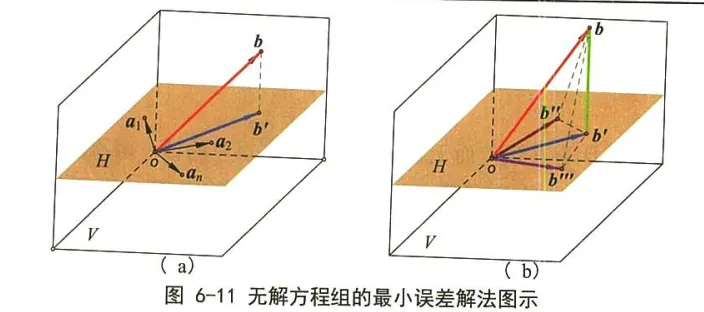
超定方程组的最小二乘解的几何解释 最小二乘法的向量解的几何意义 到现在为止,一个线性方程组 A x = b \boldsymbol{A x}=\boldsymbol{b} Ax = b b \boldsymbol{b} b A \boldsymbol{A} A
尽管不相容的方程组在数学严格的意义上不可解, 但我们还要求必须解出来它们, 即使结果是个非精确的解。最小二乘法就是这样的一个求解方法。
对于线性方程组 A x = b \boldsymbol{A} \boldsymbol{x}=\boldsymbol{b} A x = b b \boldsymbol{b} b A \boldsymbol{A} A H H H b \boldsymbol{b} b b ′ \boldsymbol{b}^{\boldsymbol{\prime}} b ′ 可以证明或看出, 这个投影 b ′ \boldsymbol{b}^{\boldsymbol{\prime}} b ′ b \boldsymbol{b} b , 因为在点 b \boldsymbol{b} b b ′ ′ \boldsymbol{b}^{\prime \prime} b ′′ b ′ ′ ′ \boldsymbol{b}^{\prime \prime \prime} b ′′′ Δ b b ′ b ′ ′ \Delta \boldsymbol{b} \boldsymbol{b}^{\prime} \boldsymbol{b}^{\prime \prime} Δ b b ′ b ′′ Δ b b ′ b ′ ′ ′ \Delta \boldsymbol{b} \boldsymbol{b}^{\prime} \boldsymbol{b}^{\prime \prime \prime} Δ b b ′ b ′′′ b b ′ \boldsymbol{b} \boldsymbol{b}^{\prime} b b ′
设向量的坐标式为 b = ( x b 1 , x b 2 , … , x b n ) , b ′ = ( x b 1 ′ , x b 2 ′ , ⋯ , x b n ′ ) \boldsymbol{b}=\left(x_{b 1}, x_{b 2}, \ldots, x_{b n}\right), \boldsymbol{b}^{\prime}=\left(x_{b 1}^{\prime}, x_{b 2}^{\prime}, \cdots, x_{b n}^{\prime}\right) b = ( x b 1 , x b 2 , … , x bn ) , b ′ = ( x b 1 ′ , x b 2 ′ , ⋯ , x bn ′ ) b \boldsymbol{b} b b ′ \boldsymbol{b}^{\prime} b ′
b b ′ → = b − b ′ = ( x b 1 − x b 1 ′ , x b 2 − x b 2 ′ , ⋯ , x b n − x b n ′ ) \overrightarrow{\boldsymbol{b b}^{\prime}}=\boldsymbol{b}-\boldsymbol{b}^{\prime}=\left(x_{b 1}-x_{b 1}^{\prime}, x_{b 2}-x_{b 2}^{\prime}, \cdots, x_{b n}-x_{b n}^{\prime}\right) bb ′ = b − b ′ = ( x b 1 − x b 1 ′ , x b 2 − x b 2 ′ , ⋯ , x bn − x bn ′ ) 其长度的平方就是
∣ b b → ∣ 2 = ( x b 1 − x b 1 ′ ) 2 + ( x b 2 − x b 2 ′ ) 2 + ⋯ + ( x b n − x b n ′ ) 2 |\overrightarrow{b \boldsymbol{b}}|^2=\left(x_{b 1}-x_{b 1}^{\prime}\right)^2+\left(x_{b 2}-x_{b 2}^{\prime}\right)^2+\cdots+\left(x_{b n}-x_{b n}^{\prime}\right)^2 ∣ b b ∣ 2 = ( x b 1 − x b 1 ′ ) 2 + ( x b 2 − x b 2 ′ ) 2 + ⋯ + ( x bn − x bn ′ ) 2 长度最小等价于长度的平方最小。现在看来这个最小误差是以平方和最小的形式来评估的,因此称为最小二乘法 。
总结, 方程组 A x = b \boldsymbol{A x}=\boldsymbol{b} Ax = b A x = b ′ \boldsymbol{A x}=\boldsymbol{b}^{\prime} Ax = b ′
一般最小二乘解的公式推导 一般地, 方程组 A x = b \boldsymbol{A x}=\boldsymbol{b} Ax = b b − b ′ \boldsymbol{b}-\boldsymbol{b}^{\prime} b − b ′ A \boldsymbol{A} A A \boldsymbol{A} A b − b ′ \boldsymbol{b}-\boldsymbol{b}^{\prime} b − b ′ A \boldsymbol{A} A
A T ( b − b ′ ) = 0 \boldsymbol{A}^{\mathrm{T}}\left(\boldsymbol{b}-\boldsymbol{b}^{\prime}\right)=\mathbf{0} A T ( b − b ′ ) = 0 把 A x = b ′ \boldsymbol{A} \boldsymbol{x}=\boldsymbol{b}^{\prime} A x = b ′ A T ( b − A x ) = 0 \boldsymbol{A}^{\mathrm{T}}(\boldsymbol{b}-\boldsymbol{A x})=\mathbf{0} A T ( b − Ax ) = 0
A T A x = A T b \boldsymbol{A}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{x}=\boldsymbol{A}^{\mathrm{T}} \boldsymbol{b} A T A x = A T b 这个方程组的解就是原方程组的最小二乘解。解出这个方程组, 问题就搞定了。
进一步, 如果 A T A \boldsymbol{A}^{\mathrm{T}} \boldsymbol{A} A T A
x = ( A T A ) − 1 A T b \boldsymbol{x}=\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}\right)^{-1} \boldsymbol{A}^{\mathrm{T}} \boldsymbol{b} x = ( A T A ) − 1 A T b 最小二乘解的例析 下面我们看一个例子, 由此了解最小二乘解的解析上的几何意义。
例在科学或工程中的一项任务就是分析或理解一些数量变化之间的联系, 其中一些数量的点列形成的图形近似接近于直线。比如在向火星发射探测器时, 我们每隔一段时间测量一下探测器到地球的距离。在这种情况下, t t t y y y V V V y = Y 0 + V t y=Y_0+V t y = Y 0 + V t m m m
{ Y 0 + V t 1 = y 1 Y 0 + V t 2 = y 2 ⋮ Y 0 + V t m = y m \left\{\begin{array}{c}
Y_0+V t_1=y_1 \\
Y_0+V t_2=y_2 \\
\vdots \\
Y_0+V t_m=y_m
\end{array}\right. ⎩ ⎨ ⎧ Y 0 + V t 1 = y 1 Y 0 + V t 2 = y 2 ⋮ Y 0 + V t m = y m 这是一个超定方程组, 因存在误差而无解 (如果不存在误差的话, 两次测量就可以搞定直线方程了)。因有两个未知数 Y 0 、 V Y_0 、 V Y 0 、 V m m m m m m
[ 1 t 1 1 t 2 ⋮ ⋮ 1 t m ] ( Y 0 V ) = ( y 1 y 2 ⋮ y m ) \left[\begin{array}{cc}
1 & t_1 \\
1 & t_2 \\
\vdots & \vdots \\
1 & t_m
\end{array}\right]\left(\begin{array}{l}
Y_0 \\
V
\end{array}\right)=\left(\begin{array}{c}
y_1 \\
y_2 \\
\vdots \\
y_m
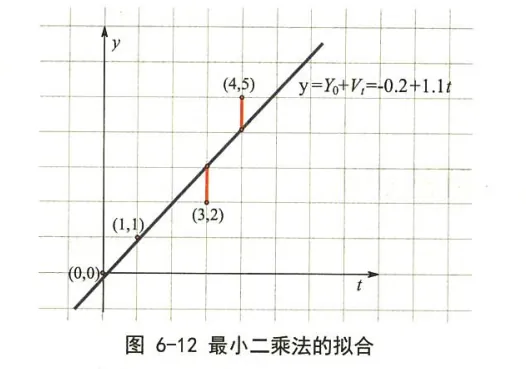
\end{array}\right) 1 1 ⋮ 1 t 1 t 2 ⋮ t m ( Y 0 V ) = y 1 y 2 ⋮ y m 假设测量了 4 组时间和距离的数据 ( t , y ) (t, y) ( t , y ) ( 0 , 0 ) 、 ( 1 , 1 ) 、 ( 3 , 2 ) 、 ( 4 , 5 ) (0,0) 、(1,1) 、(3,2) 、(4,5) ( 0 , 0 ) 、 ( 1 , 1 ) 、 ( 3 , 2 ) 、 ( 4 , 5 )
[ 1 0 1 1 1 3 1 4 ] ( Y 0 V ) = ( 0 1 2 5 ) \left[\begin{array}{ll}
1 & 0 \\
1 & 1 \\
1 & 3 \\
1 & 4
\end{array}\right]\left(\begin{array}{l}
Y_0 \\
V
\end{array}\right)=\left(\begin{array}{l}
0 \\
1 \\
2 \\
5
\end{array}\right) 1 1 1 1 0 1 3 4 ( Y 0 V ) = 0 1 2 5 对应于 A x = b \boldsymbol{A} \boldsymbol{x}=\boldsymbol{b} A x = b A T A \boldsymbol{A}^{\mathrm{T}} \boldsymbol{A} A T A
A T A = [ 1 1 1 1 0 1 3 4 ] [ 1 0 1 1 1 3 1 4 ] = [ 4 8 8 26 ] , ( A T A ) − 1 = 1 20 [ 13 − 4 − 4 2 ] \boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}=\left[\begin{array}{llll}
1 & 1 & 1 & 1 \\
0 & 1 & 3 & 4
\end{array}\right]\left[\begin{array}{ll}
1 & 0 \\
1 & 1 \\
1 & 3 \\
1 & 4
\end{array}\right]=\left[\begin{array}{cc}
4 & 8 \\
8 & 26
\end{array}\right], \quad\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}\right)^{-1}=\frac{1}{20}\left[\begin{array}{cc}
13 & -4 \\
-4 & 2
\end{array}\right] A T A = [ 1 0 1 1 1 3 1 4 ] 1 1 1 1 0 1 3 4 = [ 4 8 8 26 ] , ( A T A ) − 1 = 20 1 [ 13 − 4 − 4 2 ] 于是由最小二乘解公式
(6-9) 得
( Y 0 V ) = ( A T A ) − 1 A T b = 1 20 [ 13 − 4 − 4 2 ] [ 1 1 1 1 0 1 3 4 ] ( 0 1 2 5 ) = ( − 0.2 1.1 ) \left(\begin{array}{l}
Y_0 \\
V
\end{array}\right)=\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}\right)^{-1} \boldsymbol{A}^{\mathrm{T}} \boldsymbol{b}=\frac{1}{20}\left[\begin{array}{cc}
13 & -4 \\
-4 & 2
\end{array}\right]\left[\begin{array}{llll}
1 & 1 & 1 & 1 \\
0 & 1 & 3 & 4
\end{array}\right]\left(\begin{array}{l}
0 \\
1 \\
2 \\
5
\end{array}\right)=\left(\begin{array}{c}
-0.2 \\
1.1
\end{array}\right) ( Y 0 V ) = ( A T A ) − 1 A T b = 20 1 [ 13 − 4 − 4 2 ] [ 1 0 1 1 1 3 1 4 ] 0 1 2 5 = ( − 0.2 1.1 ) 因此最佳拟合直线为 y = − 0.2 + 1.1 t y=-0.2+1.1 t y = − 0.2 + 1.1 t y i y_i y i
[本章完]