18._基变换的几何意义

基变换的几何意义

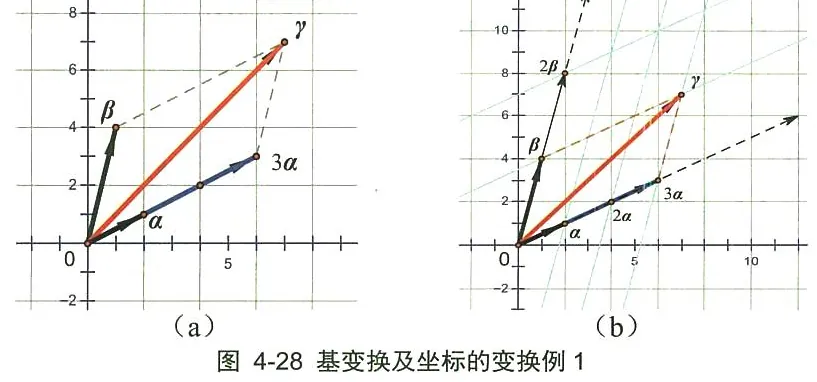
在直角平面坐标系（实际上为单位正交基 i,ji , j ）的空间中，有两个向量 α=(2,1)\alpha =(2,1) 和 β=(1,4)\beta =(1,4) ，如图 4-28（a）所示。这两个向量线性无关（不成倍数关系），让它们构成平面空间一对新基。有另外一个向量 γ=(7,7)\gamma=(7,7), 则可以把它拼凑为这两个新基的线性组合（而且组合是唯一的）:

γ=3α+β\gamma=3 \alpha+\beta

那么, 向量 γ\gamma 相对于基 α,β\alpha , \beta 的坐标向量为 (3,1)(3,1) 。

图 4-28 (a) 为原坐标系下的三个向量, 向量 γ\gamma 可以通过扩张 α\alpha 到三倍, 并与 β\beta 合并而成;根据向量的平行四边形法则，图4-28（b）为重新划分的坐标网络(图中的倾斜线，画的不清楚，请仔细看)，可以看出，向量 γ\gamma 在新网络下的坐标值确实是 (3,1)(3,1) 。

图片

基变换及坐标变换的公式

前面的讨论告诉我们，在一个 nn 维的线性空间中，可以取不同的 nn 元素无关向量组作为基。那么这个线性空间的任意两个基之间必有关联，这个关联是什么？还有，一个向量 aa 在一个确定的基下有一个确定的坐标，这个向量在不同的基下有不同的坐标。第二个问题是，同一个向量，在任意两个基上的坐标之间有什么关联？

第一个问题：两个不同基的关系 一个 nn 维线性空间 V,α1,α2,⋯ ,αnV, \boldsymbol{\alpha _1, \alpha _2, \cdots, \alpha _n} 和 β1,β2,⋯ ,βn\boldsymbol{\beta _1, \beta _2, \cdots, \beta _n} 是 VV 的两个基。先将 α1,α2,⋯ ,αn\boldsymbol{\alpha _1, \alpha _2, \cdots, \alpha _n} 作为空间的基, 那么向量组 β1,β2,⋯ ,βn\boldsymbol{\beta _1, \beta _2, \cdots, \beta _n} 可以由 α1,α2,⋯ ,αn\boldsymbol{\alpha _1, \alpha _2, \cdots, \alpha _n} 线性表示为

β1=a11α1+a12α2+⋯+a1nαn=(α1,α2,⋯ ,αn)(a11a12⋮a1n)=(a11,a12,⋯ ,a1n)(α1α2⋮αn)β2=a21α1+a22α2+⋯+a2nαn=(α1,α2,⋯ ,αn)(a21a22⋮a2n)=(a21,a22,⋯ ,a2n)(α1α2⋮αn)⋮βn=an1α1+an2α2+⋯+annαn=(α1,α2,⋯ ,αn)(an1an2⋮ann)=(an1,an2,⋯ ,ann)(α1α2⋮αn) 将以上 n 个表示式合并为 （注意：按列放）(β1,β2,⋯ ,βn)=(α1,α2,⋯ ,αn)[a11a21…an1a12a22…an2⋮⋮⋮⋮a1na2n…ann]...(4.1)\begin{aligned} &\begin{gathered} \boldsymbol{\beta}_1 = a_{11} \boldsymbol{\alpha}_1 + a_{12} \boldsymbol{\alpha}_2 + \cdots + a_{1n} \boldsymbol{\alpha}_n = \left( \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_n \right) \left( \begin{array}{c} a_{11} \\ a_{12} \\ \vdots \\ a_{1n} \end{array} \right) = \left( a_{11}, a_{12}, \cdots, a_{1n} \right) \left( \begin{array}{c} \boldsymbol{\alpha}_1 \\ \boldsymbol{\alpha}_2 \\ \vdots \\ \boldsymbol{\alpha}_n \end{array} \right) \\ \boldsymbol{\beta}_2 = a_{21} \boldsymbol{\alpha}_1 + a_{22} \boldsymbol{\alpha}_2 + \cdots + a_{2n} \boldsymbol{\alpha}_n = \left( \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_n \right) \left( \begin{array}{c} a_{21} \\ a_{22} \\ \vdots \\ a_{2n} \end{array} \right) = \left( a_{21}, a_{22}, \cdots, a_{2n} \right) \left( \begin{array}{c} \boldsymbol{\alpha}_1 \\ \boldsymbol{\alpha}_2 \\ \vdots \\ \boldsymbol{\alpha}_n \end{array} \right) \\ \vdots \\ \boldsymbol{\beta}_n = a_{n1} \boldsymbol{\alpha}_1 + a_{n2} \boldsymbol{\alpha}_2 + \cdots + a_{nn} \boldsymbol{\alpha}_n = \left( \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_n \right) \left( \begin{array}{c} a_{n1} \\ a_{n2} \\ \vdots \\ a_{nn} \end{array} \right) = \left( a_{n1}, a_{n2}, \cdots, a_{nn} \right) \left( \begin{array}{c} \boldsymbol{\alpha}_1 \\ \boldsymbol{\alpha}_2 \\ \vdots \\ \boldsymbol{\alpha}_n \end{array} \right) \end{gathered}\\ &\text { 将以上 } n \text { 个表示式合并为 （注意：按列放）}\\ &\left( \boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \cdots, \boldsymbol{\beta}_n \right) = \left( \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \cdots, \boldsymbol{\alpha}_n \right) \left[ \begin{array}{cccc} a_{11} & a_{21} & \ldots & a_{n1} \\ a_{12} & a_{22} & \ldots & a_{n2} \\ \vdots & \vdots & \vdots & \vdots \\ a_{1n} & a_{2n} & \ldots & a_{nn} \end{array} \right] ...(4.1) \end{aligned}

因为 AX=BAX=B取转置后为XTAT=BX^T A^T=B 所以，对上面矩阵取转置得

(β1β2⋮βn)=[a11a12…a1na21a22⋯a2n⋮⋮⋮an1an2…ann](α1α2⋮αn)...(4.2)\left(\begin{array}{c} \boldsymbol{\beta _1} \\ \boldsymbol{\beta _2} \\ \vdots \\ \boldsymbol{\beta_n} \end{array}\right)=\left[\begin{array}{cccc} a_{11} & a_{12} & \ldots & a_{1 n} \\ a_{21} & a_{22} & \cdots & a_{2 n} \\ \vdots & \vdots & & \vdots \\ a_{n 1} & a_{n 2} & \ldots & a_{n n} \end{array}\right]\left(\begin{array}{c} \boldsymbol{\alpha _1} \\ \boldsymbol{\alpha _2} \\ \vdots \\ \boldsymbol{\alpha _n} \end{array}\right) ...(4.2)

式（4-1）或式（4-2）称为由基 α1,α2,⋯ ,αn\alpha _1, \alpha _2, \cdots, \alpha _n 到基 β1,β2,⋯ ,βn\beta _1, \beta _2, \cdots, \beta _n 的基变换公式，其中，矩阵

P=[a11a21…an1a12a22…an2⋮⋮⋮a1na2n…ann] 或 P′=[a11a12…a1na21a22…a2n⋮⋮⋮an1an2…ann]P =\left[\begin{array}{cccc} a_{11} & a_{21} & \ldots & a_{n 1} \\ a_{12} & a_{22} & \ldots & a_{n 2} \\ \vdots & \vdots & & \vdots \\ a_{1 n} & a_{2 n} & \ldots & a_{n n} \end{array}\right] \text { 或 } P ^{\prime}=\left[\begin{array}{cccc} a_{11} & a_{12} & \ldots & a_{1 n} \\ a_{21} & a_{22} & \ldots & a_{2 n} \\ \vdots & \vdots & & \vdots \\ a_{n 1} & a_{n 2} & \ldots & a_{n n} \end{array}\right]

为A到B的过渡矩阵。

提示，上面采用抽象推导，也可以参考 向量组的等价 理解

注意两点: （1） PP 和 P′P ^{\prime} 互为转置矩阵，这取决于你将基向量 αi\alpha _i 和 βi\beta _i 看做是行向量还是列向量; （2）过渡矩阵 PP 的列向量和 P′P ^{\prime} 的行向量分别是 β1,β2,⋯ ,βn\beta _1, \beta _2, \cdots, \beta _n 在基 α1,α2,⋯ ,αn\alpha _1, \alpha _2, \cdots, \alpha _n 上的坐标 (按序排列成矩阵), 换句话说, 把 βi\beta _i 在基 α1,α2,⋯ ,αn\alpha _1, \alpha _2, \cdots, \alpha _n 上的坐标一列列地排列而成过渡矩阵 PP 。

以上得到的矩阵 PP 和 P′P ^{\prime} 给出了第一个问题的答案, 就是线性空间的两个基之间是可以互相转换或变换的, 变换的矩阵称为过渡矩阵。

同一个向量不同坐标的关系

第二个问题：同一个向量，不同坐标的关系 下面我们看看一个向量的坐标的转换是什么? 设向量 aa 在两个基 α1,α2,⋯ ,αn\alpha _1, \alpha _2, \cdots, \alpha _n 和 β1,β2,⋯ ,βn\beta _1, \beta _2, \cdots, \beta _n 下的坐标分别是 (x1,x2,⋯ ,xn)\left(x_1, x_2, \cdots, x_n\right) 和 (x1′,x2′,⋯ ,xn′)\left(x_1^{\prime}, x_2^{\prime}, \cdots, x_n^{\prime}\right), 则向量 aa 在基 α1,α2,⋯ ,αn\alpha _1, \alpha _2, \cdots, \alpha _n 上表示为

a=(x1,x2,⋯ ,xn)(a1a2⋮αn)=(a1,α2,⋯ ,αn)(x1x2⋮xn)...(4.3)a =\left(x_1, x_2, \cdots, x_n\right)\left(\begin{array}{c} a _1 \\ a _2 \\ \vdots \\ \alpha _n \end{array}\right)=\left( a _1, \alpha _2, \cdots, \alpha _n\right)\left(\begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array}\right) ...(4.3)

同时, 向量 aa 在基 β1,β2,⋯ ,βn\beta _1, \beta _2, \cdots, \beta _n 上表示为

a=(x1′,x2′,⋯ ,xn′)(β1β2⋮βn)=(β1,β2,⋯ ,βn)(x1′x2⋮xn′)...(4.4)a =\left(x_1^{\prime}, x_2^{\prime}, \cdots, x_n^{\prime}\right)\left(\begin{array}{c} \beta _1 \\ \beta _2 \\ \vdots \\ \beta _n \end{array}\right)=\left( \beta _1, \beta _2, \cdots, \beta _n\right)\left(\begin{array}{c} x_1^{\prime} \\ x_2 \\ \vdots \\ x_n^{\prime} \end{array}\right) ...(4.4)

把前面的基变换公式（4-2）和公式（4-1）代入式（4-4）得到

a=(x1′,x2′,⋯ ,xn′)P′(α1α2⋮αn)=(α1,α2,⋯ ,αn)P(x1′x2′⋮xn′)...(4.5)a =\left(x_1^{\prime}, x_2^{\prime}, \cdots, x_n^{\prime}\right) P ^{\prime}\left(\begin{array}{c} \alpha _1 \\ \alpha _2 \\ \vdots \\ \alpha _n \end{array}\right)=\left( \alpha _1, \alpha _2, \cdots, \alpha _n\right) P \left(\begin{array}{c} x_1^{\prime} \\ x_2^{\prime} \\ \vdots \\ x_n^{\prime} \end{array}\right) ...(4.5)

因为一个向量在同一个基下的坐标是唯一的, 所以, 对比式（4-5）和式（4-3）中的坐标部分，得到

(x1,x2,⋯ ,xn)=(x1′,x2′,⋯ ,xn′)P′...(4.6)\left(x_1, x_2, \cdots, x_n\right)=\left(x_1^{\prime}, x_2^{\prime}, \cdots, x_n^{\prime}\right) P^{\prime} ...(4.6)

或

(x1x2⋮xn)=P(x1′x2′⋮xn′)...(4.7)\left(\begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array}\right)= P \left(\begin{array}{c} x_1^{\prime} \\ x_2^{\prime} \\ \vdots \\ x_n^{\prime} \end{array}\right) ...(4.7)

至此，我们得到了坐标转换的公式。 假设已知坐标 (x1′,x2′,⋯ ,xn′)\left(x_1^{\prime}, x_2^{\prime}, \cdots, x_n^{\prime}\right) ，直接使用式（4-7）即得到新基下的坐标 (x1,x2,⋯ ,xn)\left(x_1, x_2, \cdots, x_n\right) 。反之，如果已知 (x1,x2,⋯ ,xn)\left(x_1, x_2, \cdots, x_n\right) 求 (x1′,x2′,⋯ ,xn′)\left(x_1^{\prime}, x_2^{\prime}, \cdots, x_n^{\prime}\right) ，即公式

(x1′x2′⋮xn′)=P−1(x1x2⋮xn)...(4.8)\left(\begin{array}{c} x_1^{\prime} \\ x_2^{\prime} \\ \vdots \\ x_n^{\prime} \end{array}\right)= P ^{-1}\left(\begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array}\right) ...(4.8)

在上述推导中，一并给出了行向量和列向量的情形。不过大多教材只处理列向量的情形，我们以后也只处理列向量, 或把向量统统默认为列向量。

基过渡矩阵和向量转换矩阵请注意一个容易搞错的地方：在列向量的习惯下，由旧基矩阵计算得到新基矩阵的变换矩阵是基过渡矩阵或转换矩阵 PP ，公式为式（4-1），右乘旧基矩阵；而任一个向量由其旧坐标计算新坐标的公式是式（4-8），其向量坐标的转换矩阵是 P−1P ^{-1} 左乘向量，用的是基过渡矩阵的逆阵。

下面我们举例说明具体的基过渡矩阵和坐标转换计算。 如图 4-29 所示，二维平面空间的一组基为 a1、α2a _1 、 \alpha _2 （没有具体值），平面有一向量 aa ，由图知 a=(−2,2)Ta =(-2,2)^{ T } 。我们再取一组基 β1、β2\beta _1 、 \beta _2, 新基在原来基 α1\alpha _1 、 α2\alpha _2 上的坐标分别是 (−12,32)T\left(-\frac{1}{2}, \frac{3}{2}\right)^{ T }, (−1,−1)T(-1,-1)^{ T } 。把它们按顺序排列起来，得到了由基 α1、α2\alpha _1 、 \alpha _2 过渡到基 β1、β2\beta _1 、 \beta _2 的过渡矩阵为

P=[−12−132−1]P =\left[\begin{array}{c:c} -\frac{1}{2} & -1 \\ \frac{3}{2} & -1 \end{array}\right]

图片

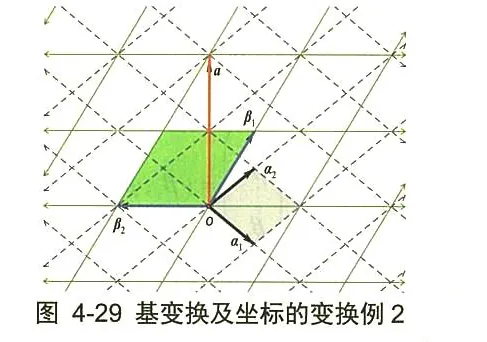
过渡矩阵也可以由列出的基的表示式方程组得到。把 β1=−12α1+32α2,β2=−α1−α2\beta _1=-\frac{1}{2} \alpha _1+\frac{3}{2} \alpha _2, \beta _2=- \alpha _1- \alpha _2 按列向量排列即可析出过渡矩阵

(β1,β2)=(α1,α2)[−12−132−1]\left( \beta _1, \beta _2\right)=\left( \alpha _1, \alpha _2\right)\left[\begin{array}{rr} -\frac{1}{2} & -1 \\ \frac{3}{2} & -1 \end{array}\right]

过渡矩阵对不对，我们验证一下。用过渡矩阵求向量 a=(−2,2)Ta =(-2,2)^{ T } 在新基 β1,β2\beta _1, \beta _2 上的坐标，用坐标转换公式：

(x1′x2′)=P−1(x1x2)=[−12−132−1]−1(−22)=12[−11−32−12](−22)=(21)\binom{x_1^{\prime}}{x_2^{\prime}}= P ^{-1}\binom{x_1}{x_2}=\left[\begin{array}{rr} -\frac{1}{2} & -1 \\ \frac{3}{2} & -1 \end{array}\right]^{-1}\binom{-2}{2}=\frac{1}{2}\left[\begin{array}{cc} -1 & 1 \\ -\frac{3}{2} & -\frac{1}{2} \end{array}\right]\binom{-2}{2}=\binom{2}{1}

看看图 4-29, 向量 aa 在基 β1、β2\beta _1 、 \beta _2 的坐标网络中的坐标正是 (21)\binom{2}{1} ，过渡矩阵和坐标转换公式得到验证。

上一章17._基变换与坐标变换_过渡矩阵
下一章19._基变换与坐标变换动画演示