5._方差与标准差

数学期望体现了随机变量取值的平均水平，它是随机变量的重要数字特征．但仅仅知道数学期望是不够的，还需要知道随机变量取值的波动程度，即随机变量所取的值与它的数学期望的偏离程度．例如，有一批电子管，其平均寿命 E(X)=10000 hE(X)=10000 \mathrm{~h} ，但仅由这一指标还不能判断这批电子管质量的好坏，还需考察电子管寿命 XX 与 E(X)E(X) 的偏离程度，若偏离程度较小，则电子管质量比较稳定。因此，研究随机变量与其平均值的偏离程度是十分重要的。那么用什么量去表示这种偏离程度呢？显然，可用随机变量 ∣X−E(X)∣|X-E(X)| 的平均值 E[∣X−E(X)∣]E[|X-E(X)|] 来表示，但为了运算方便，通常用 E{[X−E(X)]2}E\left\{[X-E(X)]^2\right\} 来表示 XX 与 E(X)E(X) 的偏离程度．

通俗来说，它描述了一组数据偏离平均值的程度。 想象两个班级考试平均分都是70分：甲班：大部分学生成绩在65-75分之间 → 方差小。乙班：一半学生考50分，另一半考90分 → 方差大。

方差的定义

设 XX 是一个随机变量，如果 E[(X−E(X))2]E\left[(X-E(X))^2\right] 存在，则称

D(X)=E[(X−E(X))2]D(X) = E\left[(X-E(X))^2\right]

为随机变量 XX 的方差。

称方差的算术平方根 σX=D(X)\sigma_X =\sqrt{D(X)} 为随机变量的标准差。

离散型

当 XX 为离散型随机变量，其概率函数为 P(X=xi)=pi,i=1,2,⋯P\left(X=x_i\right)=p_i, \quad i=1,2, \cdots, 如果级数 ∑i[xi−E(X)]2pi\sum_i\left[x_i-E(X)\right]^2 p_i 收敛，则 XX 的方差为 D(X)=∑i[xi−E(X)]2piD(X)=\sum_i\left[x_i-E(X)\right]^2 p_i;

连续型

当 XX 为连续型随机变量，其概率密度为 f(x)f(x) ，如果广义积分

∫−∞+∞[x−E(X)]2f(x)dx\int_{-\infty}^{+\infty}[x-E(X)]^2 f(x) d x

收敛，则 XX 的方差为

D(X)=∫−∞+∞[x−E(X)]2f(x)dx.D(X)=\int_{-\infty}^{+\infty}[x-E(X)]^2 f(x) d x .

在实际计算方差时，我们更多的是使用下列公式，这样更简便，

D(X)=E(X2)−[E(X)]2\boxed{ D(X) =E\left(X^2\right)-[E(X)]^2 }

证明：

D(X)=E[X−E(X)]2=E{X2−2XE(X)+[E(X)]2}=E(X2)−2E[XE(X)]+E[E(X)]2=E(X2)−2E(X)E(X)+[E(X)]2=E(X2)−[E(X)]2\begin{aligned} D(X) & =E[X-E(X)]^2 \\ & =E\left\{X^2-2 X E(X)+[E(X)]^2\right\} \\ & =E\left(X^2\right)-2 E[X E(X)]+E[E(X)]^2 \\ & =E\left(X^2\right)-2 E(X) E(X)+[E(X)]^2 \\ & =E\left(X^2\right)-[E(X)]^2 \end{aligned}

例 设有甲、乙两种棉花，从中各抽取等量的样品进行检验，结果如下： 图片

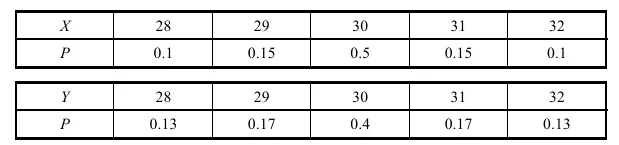
其中 X、YX 、 Y 分别表示甲、乙两种棉花的纤维的长度（单位： mm ），求 D(X)D(X) 与 D(Y)D(Y) ，并评定它们的质量。

解 由于

E(X)=28×0.1+29×0.15+30×0.5+31×0.15+32×0.1=30E(Y)=28×0.13+29×0.17+30×0.4+31×0.17+32×0.13=30\begin{gathered} E(X)=28 \times 0.1+29 \times 0.15+30 \times 0.5+31 \times 0.15+32 \times 0.1=30 \\ E(Y)=28 \times 0.13+29 \times 0.17+30 \times 0.4+31 \times 0.17+32 \times 0.13=30 \end{gathered}

故得

D(X)=(28−30)2×0.1+(29−30)2×0.15+(30−30)2×0.5+(31−30)2×0.15+(32−30)2×0.1=4×0.1+1×0.15+0×0.5+1×0.15+4×0.1=1.1,D(Y)=(28−30)2×0.13+(29−30)2×0.17+(30−30)2×0.4+(31−30)2×0.17+(32−30)2×0.13=4×0.13+1×0.17+0×0.4+1×0.17+4×0.13=1.38.\begin{aligned} D(X) & =(28-30)^2 \times 0.1+(29-30)^2 \times 0.15+(30-30)^2 \times 0.5+(31-30)^2 \times 0.15+(32-30)^2 \times 0.1 \\ & =4 \times 0.1+1 \times 0.15+0 \times 0.5+1 \times 0.15+4 \times 0.1=1.1, \\ D(Y) & =(28-30)^2 \times 0.13+(29-30)^2 \times 0.17+(30-30)^2 \times 0.4+(31-30)^2 \times 0.17+(32-30)^2 \times 0.13 \\ & =4 \times 0.13+1 \times 0.17+0 \times 0.4+1 \times 0.17+4 \times 0.13=1.38 . \end{aligned}

因 D(X)<D(Y)D(X)<D(Y) ，所以甲种棉花纤维长度的方差小些，说明其纤维长度变化要小些，也就是要均匀些，故甲种棉花质量较好。

例 设随机变量 XX 的概率密度为

f(X)={1+x,−1⩽x<01−x,0⩽x<10, 其他 ,f(X)=\left\{\begin{array}{ll} 1+x, & -1 \leqslant x<0 \\ 1-x, & 0 \leqslant x<1 \\ 0, & \text { 其他 } \end{array},\right.

求 D(X)D(X) ．

解

E(X)=∫−10x(1+x)dx+∫01x(1−x)dx=0E(X2)=∫−10x2(1+x)dx+∫01x2(1−x)dx=1/6D(X)=E(X2)−[E(X)]2=1/6\begin{gathered} E(X)=\int_{-1}^0 x(1+x) d x+\int_0^1 x(1-x) d x=0 \\ E\left(X^2\right)=\int_{-1}^0 x^2(1+x) d x+\int_0^1 x^2(1-x) d x=1 / 6 \\ D(X)=E\left(X^2\right)-[E(X)]^2=1 / 6 \end{gathered}

例 求 均匀分布：X∼U(a,b)X \sim U(a, b) 方差

解： XX 的概率密度为 f(x)={1b−a,a<x<b0, 其他 f(x)=\left\{\begin{array}{ll}\frac{1}{b-a}, & a<x<b \\ 0, & \text { 其他 }\end{array}\right. ，而 E(X)=∫−∞+∞xf(x)dx=∫abxb−adx=a+b2E(X)=\int_{-\infty}^{+\infty} x f(x) d x=\int_a^b \frac{x}{b-a} d x=\frac{a+b}{2} ，故所求方差为

D(X)=E(X2)−[E(X)]2=∫abx21b−adx−(a+b2)2=(b−a)212.D(X)=E\left(X^2\right)-[E(X)]^2=\int_a^b x^2 \frac{1}{b-a} d x-\left(\frac{a+b}{2}\right)^2=\frac{(b-a)^2}{12} .

例 正态分布：X∼N(μ,σ2)X \sim N\left(\mu, \sigma^2\right) 先求标准正态变量 Z=X−μσZ=\frac{X-\mu}{\sigma} 的数学期望和方差．因为 ZZ 的概率密度为

ϕ(z)=12πe−z2/2,−∞<z<+∞\phi(z)=\frac{1}{\sqrt{2 \pi}} e^{-z^2 / 2}, \quad-\infty<z<+\infty

于是 E(Z)=0E(Z)=0 ，

D(Z)=E(Z2)=12π∫−∞+∞z2e−z2/2dz=−12π∫−∞+∞zd(e−z2/2)=−z2πe−z2/2∣−∞+∞+12π∫−∞+∞e−z2/2dz=1π∫−∞+∞e−(z/2)2d(z2)=1,\begin{aligned} D(Z) & =E\left(Z^2\right)=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{+\infty} z^2 e^{-z^2 / 2} d z=-\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{+\infty} z d\left(e^{-z^2 / 2}\right) \\ & =-\left.\frac{z}{\sqrt{2 \pi}} e^{-z^2 / 2}\right|_{-\infty} ^{+\infty}+\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{+\infty} e^{-z^2 / 2} d z=\frac{1}{\sqrt{\pi}} \int_{-\infty}^{+\infty} e^{-(z / \sqrt{2})^2} d\left(\frac{z}{\sqrt{2}}\right)=1, \end{aligned}

其中利用泊松积分 ∫−∞+∞e−x2dx=π\int_{-\infty}^{+\infty} e ^{-x^2} d x=\sqrt{\pi} ． 因 X=μ+σZX=\mu+\sigma Z ，由数学期望和方差的性质得

E(X)=E(μ+σZ)=μD(X)=D(μ+σZ)=E[μ+σZ−E(μ+σZ)]2=E(σ2Z2)=σ2E(Z2)=σ2D(Z)=σ2\begin{gathered} E(X)=E(\mu+\sigma Z)=\mu \\ D(X)=D(\mu+\sigma Z)=E[\mu+\sigma Z-E(\mu+\sigma Z)]^2=E\left(\sigma^2 Z^2\right)=\sigma^2 E\left(Z^2\right)=\sigma^2 D(Z)=\sigma^2 \end{gathered}

或者

D(X)=D(μ+σZ)=D(μ)+D(σZ)=0+D(σZ)=σ2D(Z)=σ2D(X)=D(\mu+\sigma Z)=D(\mu)+D(\sigma Z)=0+D(\sigma Z)=\sigma^2 D(Z)=\sigma^2

这就是说，正态分布的概率密度中的两个参数 μ\mu 和 σ\sigma 分别就是该分布的数学期望和均方差，因而正态分布完全可由它的数学期望和方差所确定．

由前面知道，若 Xi∼N(μ,σ2),i=1,2,⋯ ,nX_i \sim N\left(\mu, \sigma^2\right), i=1,2, \cdots, n ，且它们相互独立，则它们的线性组合 c1X1+c2X2+⋯+cnXn(c1,c2,⋯ ,cnc_1 X_1+c_2 X_2+\cdots+c_n X_n\left(c_1, c_2, \cdots, c_n\right. 是不全为零的常数）仍然服从正态分布。于是由数学期望和方差的性质得：

c1X1+c2X2+⋯+cnXn∼N(∑i=1nciμi,∑i=1nci2σi2)c_1 X_1+c_2 X_2+\cdots+c_n X_n \sim N\left(\sum_{i=1}^n c_i \mu_i, \sum_{i=1}^n c_i^2 \sigma_i^2\right)

这是一个重要的结果．

常用分布的方差

在附表里列出了常见分布的期望和方差，详见 此处

Previous4._数学期望的性质
Next6._方差的性质