0x26 广搜变形

$\diamond$ 双端队列BFS

在最基本的广度优先搜索中，每次沿着分支的扩展都记为“一步”，我们通过逐层搜索，解决了求从起始状态到每个状态的最少步数的问题。这其实等价于在一张边权均为1的图上执行广度优先遍历，求出每个点相对于起点的最短距离（层次）。在第0x21节中我们曾讨论过这个问题，并得到了“队列中的状态的层数满足两段性和单调性”的结论。从而我们可以知道，每个状态在第一次被访问并入队时，计算出的步数即为所求。

然而，如果图上的边权不全是1呢？换句话说，如果每次扩展都有各自不同的“代价”，我们想求出起始状态到每个状态的最小代价，应该怎么办呢？我们不妨先来讨论图上的边权要么是1、要么是0的情况。

【例题】电路维修

Ha'nyu 是来自异世界的魔女，她在漫无目的地四处漂流的时候，遇到了善良的少女 Rika，从而被收留在地球上。Rika 的家里有一辆飞行车。有一天飞行车的电路板突然出现了故障，导致无法启动。

电路板的整体结构是一个 $R$ 行 $C$ 列的网格，如右图所示。每个格点都是电线的接点，每个格子都包含一个电子元件。电子元件的主要部分是一个可旋转的、连接一条对角线上的两个接点的短电缆。在旋转之后，它就可以连接另一条对角线的两个接点。电路板左上角的接点接入直流电源，右下角的接点接入飞行车的发动装置。

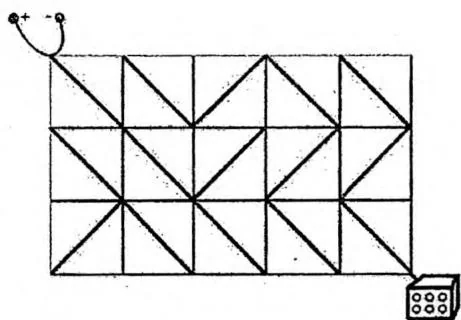
Ha'nyu发现因为某些元件的方向不小心发生了改变，电路板可能处于断路的状态。她准备通过计算，旋转最少数量的元件，使电源与发动装置通过若干条短缆相连。不过，电路的规模实在是太大了，Ha'nyu并不擅长编程，希望你能够帮她解决这个问题。

数据范围： $R,C\leq 500$ 。

我们可以把电路板上的每个格点（横线与竖线的交叉点）看作无向图中的节点。若两个节点 $x$ 和 $y$ 是某个小方格的两个对角，则在 $x$ 与 $y$ 之间连边。若该方格中的标准件（对角线）与 $x$ 到 $y$ 的线段重合，则边权为0；若垂直相交，则边权为1（说明需要旋转1次才能连上）。然后，我们在这个无向图中求出左上角到右下角的最短距离，就得到了答案。

这是一张边权要么是0、要么是1的无向图。在这样的图上，我们可以通过双端队列广搜来计算。算法的整体框架与一般的广搜类似，只是在每个节点上沿分支扩展时稍作改变。如果这条分支是边权为0的边，就把沿该分支到达的新节点从队头入队；如果这条分支是边权为1的边，就像一般的广搜一样从队尾入队。这样一来，我们就仍然能保证，任意时刻广搜队列中的节点对应的距离值都具有“两段性”和“单调性”，每个节点第一次被访问（入队）时，就能得到从左上角到该节点的最短距离。

因为每个节点只需要访问一次，所以算法的时间复杂度为 $O(R * C)$ 。

$\spadesuit$ 优先队列BFS

对于更加具有普适性的情况，也就是每次扩展都有各自不同的“代价”时，求出起始状态到每个状态的最小代价，就相当于在一张带权图上求出从起点到每个节点的最短路。此时，我们有两个解决方案：

方法一

仍然使用一般的广搜，采用一般的队列。

这时我们不再能保证每个状态第一次入队时就能得到最小代价，所以只能允许一个状态被多次更新、多次进出队列。我们不断执行搜索，直到队列为空。

整个广搜算法对搜索树进行了重复遍历与更新，直至“收敛”到最优解，其实也就是“迭代”的思想。最坏情况下，该算法的时间复杂度会从一般广搜的 $O(N)$ 增长到 $O(N^2)$ 。对应在最短路问题中，就是我们将在0x61节介绍的SPFA算法。

方法二

改用优先队列进行广搜。

这里的“优先队列”就相当于一个二叉堆。我们可以每次从队列中取出当前代价最小的状态进行扩展（该状态一定已经是最优的，因为队列中其他状态的当前代价都不

小于它，所以以后就不可能再更新它了），沿着各条分支把到达的新状态加入优先队列。不断执行搜索，直到队列为空。

在优先队列 BFS 中，每个状态也会被多次更新、多次进出队列，一个状态也可能以不同的代价在队列中同时存在。不过，当每个状态第一次从队列中被取出时，就得到了从起始状态到该状态的最小代价。之后若再被取出，则可以直接忽略，不进行扩展。所以，优先队列 BFS 中每个状态只扩展一次，时间复杂度只多了维护二叉堆的代价。若一般广搜复杂度为 $O(N)$ ，则优先队列 BFS 的复杂度为 $O(N \log N)$ 。对应在最短路问题中，就是我们将在 0x61 节介绍的堆优化的 Dijkstra 算法。

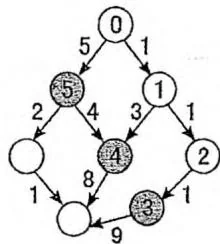
下图就展示了优先队列 BFS 的详细过程，每条边上的数值标明了每个状态向下扩展所需的代价，节点中的数值标明了每个状态上求出的“当前代价”，灰色节点标明了每个时刻在堆中出现至少一次的节点。

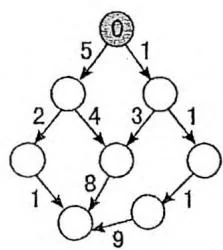
队列：0

取出：0

插入：15

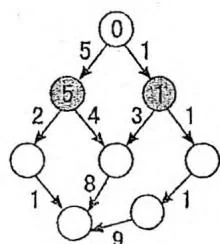
队列：15

取出：1

插入：24

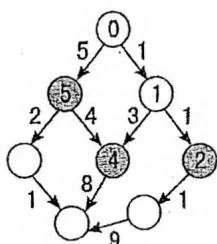
队列：245

取出：2

插入：3

队列：345

取出：3

插入：12

队列：4512

取出：4

插入：12

队列：51212

取出：5

插入：7

队列：71212

取出：7

插入：8

队列：81212

取出：8

得到答案

建议不熟悉最短路相关算法的读者，简要对0x61节的两个单源最短路径算法进行阅读，这对于理解并写出正确的优先队列BFS有很大的帮助。

至此，我们就可以对BFS的形式，按照对应在图上的边权情况进行分类总结：

1. 问题只计最少步数，等价于在边权都为1的图上求最短路。

使用普通的BFS，时间复杂度 $O(N)$ 。

每个状态只访问（入队）一次，第一次入队时即为该状态的最少步数。

1. 问题每次扩展的代价可能是 0 或 1，等价于在边权只有 0 和 1 的图上求最短路。

使用双端队列BFS，时间复杂度 $O(N)$ 。

每个状态只访问（入队）一次，第一次入队时即为该状态的最小代价。

1. 问题每次扩展的代价是任意数值，等价于一般的最短路问题。

(1) 使用优先队列 BFS，时间复杂度 $O(N \log N)$ 。

每个状态被更新（入队）多次，只扩展一次，第一次出队时即为该状态的最小代价。

(2) 使用迭代思想+普通的 BFS，时间复杂度 $O(N^{2})$ 。

每个状态被更新（入队）、扩展（出队）多次，最终完成搜索后，记录数组中保存了最小代价。

【例题】FullTank POJ3635

有 $N(1 \leq N \leq 1000)$ 个城市和 $M(1 \leq M \leq 10000)$ 条道路，构成一张无向图。在每个城市里边都有一个加油站，不同加油站的价格不一样。通过一条道路的油耗就是该道路的边权。现在你需要回答不超过 100 个问题，在每个问题中，请计算出一架油箱容量为 $C(1 \leq N \leq 100)$ 的车子，从起点 $S$ 开到终点 $T$ 至少要花多少油钱？

我们使用二元组（city, fuel）来表示每个状态，其中 city 为城市编号，fuel 为邮箱中剩余的汽油量，并使用记录数组 $d[city][fuel]$ 存储最少花费。

对于每个问题，我们都单独进行一次优先队列BFS。起始状态为 $(S,0)$ 。每个状态(city,fuel）的分支有：

1. 若 $fuel < C$ ，可以加 1 升油，扩展到新状态 (city, fuel + 1)，花费在城市 city 加 1 升油的钱。

2. 对于每条从 city 出发的边 (city, next)，若边权大小 $w$ 不超过 fuel，可以开车前往城市 next，扩展到新状态 (next, fuel - w)。

我们不断取出优先队列中“当前花费最少”的状态（堆顶）进行扩展，更新扩展到的新状态在记录数组 $d$ 中存储的值，直到终点 $T$ 的某个状态第一次被取出，即可停止BFS，输出答案。

$\spadesuit$ 双向BFS

在0x24节中我们介绍了双向搜索的思想，并讲解了一道双向DFS的例题。双向BFS的思想与之完全相同，我们就不再重复描述。因为BFS本身就是逐层搜索的算法，所以双向BFS的实现更加自然、简便。以普通的求最少步数的双向BFS为例，我们只需从起始状态、目标状态分别开始，两边轮流进行，每次各扩展一整层。当两边各自有一个状态在记录数组中发生重复时，就说明这两个搜索过程相遇了，可以合并得出起点到终点的最少步数。

【例题】Nightmare II HDOJ3085

给定一张 $N * M$ 的地图，地图中有1个男孩、1个女孩和2个鬼。字符“.”表示道路，字符“X”表示墙，字符“M”表示男孩的位置，字符“G”表示女孩的位置，字符“Z”表示鬼的位置。男孩每秒可以在道路上移动3个单位距离，女孩每秒可以在道路上移动1个单位距离。每个鬼占据的区域每秒可以向四周扩张2个单位距离，并且无视墙的阻挡，也就是在第 $k$ 秒后所有与鬼的曼哈顿距离不超过 $2k$ 的位置都会被鬼占领。

求在不进入鬼的占领区的前提下，男孩与女孩能否会合，若能会合，求出最短会合时间。 $1 \leq N, M \leq 800$ 。

使用双向BFS算法。建立两个队列，分别从男孩的初始位置、女孩的初始位置开始进行BFS，两边轮流进行。

在每一轮中，男孩这边BFS三层（可以移动三步），女孩这边BFS一层（可以移动一步），使用数组 $d$ 记录每个位置对于男孩和女孩的可达性。

当然，在BFS的每次扩展时，注意实时计算新状态与鬼之间的曼哈顿距离，如果已经小于等于当前轮数（即秒数）的2倍，那么就判定这个新状态不合法，不再记录或入队。

在BFS的过程中，第一次出现某个位置 $(x,y)$ 既能被男孩到达，也能被女孩到达时，当前轮数就是两人的最短会合时间。