0x28 IDA*

在上一节中我们提到， $\mathbf{A}^*$ 算法本质上是带有估价函数的优先队列BFS算法。故 $\mathbf{A}^*$

算法有一个显而易见的缺点，就是需要维护一个二叉堆（优先队列）来存储状态及其估价，耗费空间较大，并且对堆进行一次操作也要花费 $O(\log N)$ 的时间。

我们也提到了 $A^*$ 算法的关键在于设计估价函数。既然估价函数与优先队列 BFS 结合可以产生 $A^*$ 算法，那么估价函数能否与 DFS 结合呢？当然，DFS 也有一个缺点，就是一旦估价出现失误，容易向下递归深入一个不能产生最优解的分支，浪费许多时间。

综合以上讨论，我们最终选择把估价函数与迭代加深的DFS算法相结合。请读者回忆0x24节中学习的迭代加深DFS算法。该算法限定一个深度，在不超过该深度的前提下执行DFS，若找不到解就扩大深度限制，重新进行搜索。

我们设计一个估价函数，估算从每个状态到目标状态需要的步数。当然，与A*算法一样，估价函数需要遵守“估计值不大于未来实际步数”的准则。然后，以迭代加深DFS的搜索框架为基础，把原来简单的深度限制加强为：若当前深度+未来估计步数>深度限制，则立即从当前分支回溯。

这就是IDA算法（迭代加深的A算法）。IDA算法在许多场景下表现出了优秀的效率，并且程序实现的难度低于A算法。

【例题】Booksort FOJ3460

给定 $n (1 \leq n \leq 15)$ 本书，编号为 $1 \sim n$ 。在初始状态下，书是任意排列的。在每一次操作中，可以抽取其中连续的一段，再把这段插入到其他某个位置。我们的目标状态是把书按照 $1 \sim n$ 的顺序依次排列，求最少需要多少次操作。若操作次数 $\geq 5$ ，则直接输出字符串“5 or more”即可。

我们先来估算一下每个状态的分支数量。在每个状态下，我们可以抽取连续的一段书，移动到另一个位置。对于任意整数 $i$ ，当抽取长度为 $i$ 时，有 $n - i + 1$ 种选择方法，有 $n - i$ 个可插入的位置。另外，把一段书移动到更靠前的某个位置，等价于把“跳过”的那段书移动到靠后的某个位置，所以上面的计算方法把每种移动情况算了两遍。因此每个状态的分支数量约为： $\sum_{i=1}^{n}(n - i)*(n - i + 1) \leq (15*14 + 14*13 + \cdots + 2*1)/2 = 560$ 。

根据题目要求，我们只需要考虑在4次操作以内是否能实现目标，也就是我们只需要考虑搜索树的前4层。4层的搜索树的规模能够达到 $560^{4}$ ，无法承受。

第一种解法是采用双向BFS，从起始状态、目标状态开始各搜索2步，看能否到达相同的状态进行衔接，复杂度降低为 $560^{2}$ 。

第二种解法是采用 $\mathrm{IDA^{*}}$ 。

在目标状态下，第 $i$ 本书后边应该是第 $i + 1$ 本书，我们称 $i + 1$ 是 $i$ 的正确后继。

对于任意状态，考虑整个排列中书的错误后继的总个数（记为 $tot$ ），可以发现每

次操作至多更改3本书的后继。即使在最理想的情况下，每次操作都能把某3个错误后继全部改对，消除所有错误后继的操作次数也至少需要 $\lceil \text{tot} / 3\rceil$ （其中「]表示向上取整）次。

因此，我们把一个状态 $s$ 的估价函数设计为 $f(s) = [tot / 3]$ ，其中 $tot$ 表示在状态 $s$ 下书的错误后继总数。

我们采用迭代加深的方法，从 $1 \sim 4$ 依次限制搜索深度，然后从起始状态出发DFS。DFS时，在每个状态下直接枚举抽取哪一段、移动到更靠后的哪个位置，沿着该分支深入即可。注意在进入任何状态 $s$ 后，我们先进行判断，如果当前操作次数加上 $f(s)$ 已经大于深度限制，直接从当前分支回溯。在实际测试中，上述IDA*算法能够比双向BFS更快地求出答案。

【例题】The Rotation Game FOJ2286

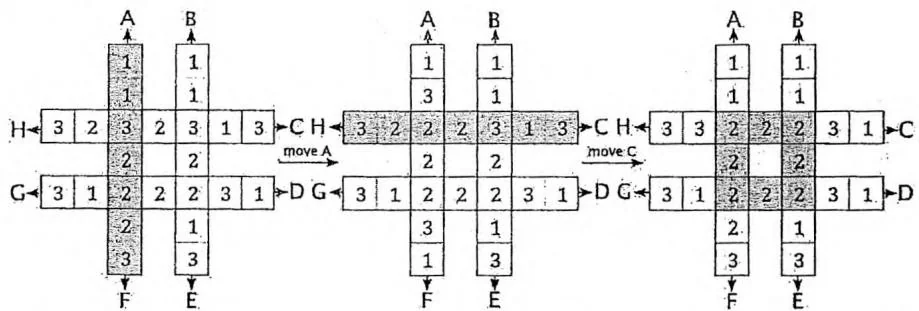
如下图所示，有一个“#”形的棋盘，上面有1，2，3三种数字各8个。给定8种操作，分别为图中的A~H。这些操作会按照图中字母和箭头所指明的方向，把一条长为8的序列循环移动1个单位。例如下图最左边的“#”形棋盘执行操作A后，会变为下图中间的“#”形棋盘，再执行操作C后会变成下图最右边的“#”形棋盘。

给定一个初始状态，请使用最少的操作次数，使“#”形棋盘最中间的8个格子里的数字相同。

可以使用IDA*算法求解。首先我们来确定DFS的框架——在每个状态下枚举执行哪种操作，然后沿着该分支深入即可。有一个很明显的剪枝是记录上一次的操作，不执行上次操作的逆操作，避免来回搜索。

接下来我们设计估价函数。通过仔细观察可以发现，在每个状态下，如果中间8个格子里出现次数最多的数字是 $k$ ，而中间8个格子里剩下的数字有 $m$ 个与 $k$ 不同，那么把中间8个格子里的数字都变为 $k$ 至少需要 $m$ 次操作。因此，我们就以这个 $m$ 为估价即可。

总而言之，我们采用迭代加深，由1开始从小到大依次限制操作次数（搜索深度），在DFS的每个状态下，若“当前操作次数+估价>深度限制”，则从当前分支回溯。

*【例题】Square Destroyer FOJ1084

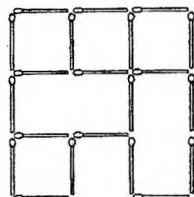
给定一个“在由火柴棒拼成的 $n * n (n \leq 5)$ 的网格图中去掉一些边”构成的图形（如右图所示）。求至少再去掉多少根火柴棒，可以使得图形中不含有正方形（内部有其他火柴的大正方形也算，例如右图中有5个正方形）。

DFS 框架：在每个状态下找出一个最小的正方形，枚举去掉它边界上的哪一根火柴棒，然后沿着该分支深入。

估价函数设计：不断从当前图形中任选一个还没有被破坏的正方形，去掉它边界上的所有火柴棒，但是只记作一次操作。按照上述方法统计出破坏所有正方形需要多少次操作，作为“从当前图形到不含有正方形的图形需要去掉的火柴棒数量”的估计值。这个估值显然不会大于未来实际需要去掉的火柴棒数。

最后执行迭代加深的 $A^{*}$ 算法（ $\mathrm{IDA^{*}}$ ）即可快速求出答案。值得提醒的是，本题作为一道选做题，代码实现中火柴棒编号、图形样式的处理较为繁琐，读者需要格外仔细。