6._平均数_众数_分位数_中位数 - 概率论与数理统计

平均数

平均数（mean）也称均值，它是一组数据相加后除以数据的个数得到的结果。平均数是度量数据集中趋势的常用统计量，在参数估计和假设检验中经常用到。

设一组样本数据为 $x_1, x_2, \cdots, x_n$ ，样本量（样本数据的个数）为 $n$ ，则样本平均数用 $\bar{x}$ 表示，计算公式为

\bar{x}=\frac{x_1+x_2+\cdots+x_n}{n}=\frac{\sum_{i=1}^n x_i}{n} ...(4.1)

式（4．1）也称为简单平均数（simple mean）。

例随机抽取 30 个消费者，得到他们每月网购金额的数据如表 4－1 所示。计算这 30 个人每月的平均网购金额。 $图片$

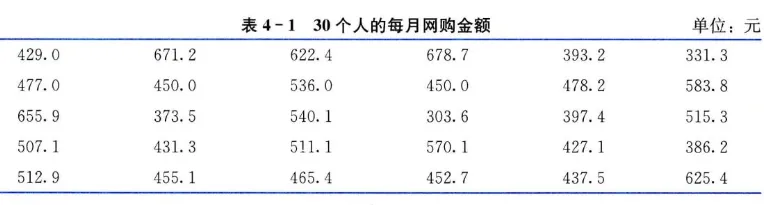
\bar{x}=\frac{429.0+671.2+\cdots+437.5+625.4}{30}=\frac{14668.5}{30}=488.95

加权平均数

假设演员唱歌，由评委和观众打分，因为评委更专业，所以评委的分数占总分的60%，而观众比较业余，其打分的权重站40%，这就是加权平均数的由来

如果样本数据被分成 $k$ 组，各组的组中值（一个组中的中间值，是组的下限值与上限值的平均数）分别用 $m_1, m_2, \cdots, m_k$ 表示，各组的频数分别用 $f_1, f_2, \cdots, f_k$ 表示，则样本平均数的计算公式为：

\bar{x}=\frac{m_1 f_1+m_2 f_2+\cdots+m_k f_k}{f_1+f_2+\cdots+f_k}=\frac{\sum_{i=1}^k m_i f_i}{n} ...(4.2)

式（4．2）也称为加权平均数（weighted mean）（1）

中位数和四分位数

一组数据从小到大排序后，找出排在某个位置上的数值，并用该数值代表数据水平的高低，则这些位置上的数值就是相应的分位数（quantile），包括中位数，四分位数等。

中位数

中位数（median）是一组数据排序后处在中间位置上的数值，用 $M_e$ 表示。中位数是用一个点将全部数据等分成两部分，每部分包含 $50 \%$ 的数据，一部分数据比中位数大，另一部分比中位数小。中位数是用中间位置上的值代表数据的水平，其特点是不受极端值的影响，在研究收人分配时很有用。

计算中位数时，要先对 $n$ 个数据从小到大进行排序，然后确定中位数的位置，最后确定中位数的具体数值。如果位置是整数值，中位数就是该位置所对应的数值；如果位置是整数加 0.5 的数值，中位数就是该位置两侧值的平均值。设一组数据 $x_1, x_2, \cdots, x_n$ 从小到大排序后为 $x_{(1)}, x_{(2)}, \cdots, x_{(n)}$ ，则中位数就是 $(n+1) / 2$ 位置上的值。计算公式为：

M_e= \begin{cases}x_{\left(\frac{n+1}{2}\right)} & n \text { 为奇数 } \\ \frac{1}{2}\left\{x_{\left(\frac{n}{2}\right)}+x_{\left(\frac{n}{2}+1\right)}\right\} & n \text { 为偶数 }\end{cases}

四分位数

四分位数（quartile）是一组数据排序后处于 $25 \%$ 和 $75 \%$ 位置上的数值。它是用 3个点将全部数据等分为 4 部分，其中每部分包含 $25 \%$ 的数据。很显然，中间的四分位数就是中位数，因此通常所说的四分位数是指处在 $25 \%$ 位置上和处在 $75 \%$ 位置上的两个数值。

与中位数的计算方法类似，计算四分位数时，首先对数据进行排序，然后确定四分位数所在的位置，该位置上的数值就是四分位数。与中位数不同的是，四分位数位置的确定方法有多种 ${ }^{(1)}$ ，每种方法得到的结果可能会有一定差异，但差异不会很大（一般相差不会超过一个位次）。由于不同软件的计算方法可能不一样，因此，对同一组数据使用不同软件得到的四分位数结果也可能会有所差异，但不会影响分析的结论。

设 $25 \%$ 位置上的四分位数为 $Q_{25 \%}, 75 \%$ 位置上的四分位数为 $Q_{75 \%}$ ，用 SPSS 计算四分位数位置的公式为：

Q_{25 \%} \text { 位置 }=\frac{n+1}{4}, \quad Q_{75 \%} \text { 位置 }=\frac{3(n+1)}{4}

如果位置是整数，四分位数就是该位置对应的数值；如果是在整数加 0.5 的位置上，则取该位置两侧数值的平均数；如果是在整数加 0.25 或 0.75 的位置上，则四分位数等于该位置前面的数值加上按比例分摊的位置两侧数值的差值。

沿用例 4．1。计算 30 个消费者每月网购金额的四分位数。－－解先对 $n$ 个数据从小到大排序，然后计算出四分位数的位置：

Q_{25 \%} \text { 位置 }=\frac{30+1}{4}=7.75, \quad Q_{75 \%} \text { 位置 }=\frac{3 \times(30+1)}{4}=23.25

$Q_{25 \%}$ 在第 7 个数值（427．1）和第 8 个数值（429．0）之间 0.75 的位置上：

Q_{25 \%}=427.1+0.75 \times(429.0-427.1)=428.525

$Q_{75 \%}$ 在第 23 个数值（540．1）和第 24 个数值（570．1）之间 0.25 的位置上：

Q_{25 \%}=540.1+0.25 \times(570.1-540.1)=547.6

由于 $Q_{25 \%}$ 和 $Q_{75 \%}$ 之间大约包含了 $50 \%$ 的数据，就上面 30 个消费者每月网购金额而言，可以说大约有一半人的每月网购金额在 $428.525 \sim 547.6$ 元之间。

众数

除平均数，中位数和四分位数外，有时候也会使用众数作为数据集中趋势的度量。众数（mode）是一组数据中出现频数最多的数值，用 $M_o$ 表示。一般情况下，只有在数据量较大时众数才有意义。从分布的角度看，众数是一组数据分布的峰值点所对应的数值。如果数据的分布没有明显的峰值，众数可能不存在；如果有两个或多个峰值，也可以有两个或多个众数。就例 4.1 而言，出现金额最多的是 450 ，因此 $M_o=450$ 。

几何平均数

几何平均数（geometric mean）是 $n$ 个变量值乘积的 $n$ 次方根，用 $G$ 表示。计算公式为

G=\sqrt[n]{x_1 \times x_2 \times \cdots \times x_n}=\sqrt[n]{\prod_{i=1}^n x_i}

式中， $\Pi$ 为连乘符号。几何平均数是适用于特殊数据的一种平均数，它主要用于计算平均比率。当所掌握的变量值本身是比率形式时，采用几何平均法计算平均比率更为合理。在实际应用中，几何平均数主要用于计算现象的平均增长率。

当数据中出现零值或负值时，不宜计算几何平均数。

例一位投资者持有一种股票，连续 4 年的收益率分别为 $4.5 \%, 2.1 \%, 25.5 \%, 1.9 \%$ 。计算该投资者在这 4 年内的平均收益率。－－解设平均收益率为 $\bar{G}$ ，有

\begin{aligned} \bar{G} & =\sqrt[n]{\prod_{i=1}^n x_i}-1 \\ & =\sqrt[4]{104.5 \% \times 102.1 \% \times 125.5 \% \times 101.9 \%-1} \\ & =8.0787 \% \end{aligned}

即该投资者的年均收益率为 $8.0787 \%$ 。假定该投资者最初投人 10000 元，按各年的几何平均收益率计算，第 4 年的本利总和应为：

\begin{aligned} & 10000 \times 104.5 \% \times 102.1 \% \times 125.5 \% \times 101.9 \% \\ & =10000 \times(108.0787 \%)^4 \\ & =13644.57(\text { 元 }) \end{aligned}

如果按算术平均计算，平均收益率则为：

\bar{G}=(4.5 \%+2.1 \%+25.5 \%+1.9 \%) \div 4=8.5 \%

按算术平均收益率计算，该投资者第 4 年的本利总和应为：

10000 \times(108.5 \%)^4=13858.59 \text { (元) }

二者相差 214.02 元，而这部分收益投资者并没有获得。这说明，对于比率数据的平均，采用几何平均要比算术平均更合理。从下面的分析中可以更清楚地看出这一点。设开始的数值为 $y_0$ ，逐年增长率为 $G_1, G_2, \cdots, G_n$ ，则第 $n$ 年的数值为：

y_n=y_0\left(1+G_1\right)\left(1+G_2\right) \cdots\left(1+G_n\right)=y_0 \prod_{i=1}^n\left(1+G_i\right) ...(4.6)

从 $y_0$ 到 $y_n$ 有 $n$ 年，每年的增长率都相同，这个增长率 $G$ 就是平均增长率 $\bar{G}$ ，即式（4．7）中的 $G_i$ 都等于 $G$ 。因此

(1+G) n=\prod_{i=1}^n\left(1+G_i\right)...(4.7)

\bar{G}=\sqrt[n]{\prod_{i=1}^n\left(1+G_i\right)}-1 ...(4.8)

当所平均的各比率数值差别不大时，算术平均和几何平均的结果相差不大；而当各比率数值相差较大时，二者的差别就很明显。

众数，中位数和平均数的比较

众数，中位数和平均数是集中趋势的三个主要测度值，它们具有不同的特点和应用场合。

从分布的角度看，众数始终是一组数据分布的最高峰值，中位数是处于一组数据中间位置上的值，而平均数则是全部数据的算术平均。因此，对于具有单峰分布的大多数数据而言，众数，中位数和平均数之间具有以下关系：如果数据的分布是对称的，众数 $\left(M_o\right)$ ，中位数 $\left(M_e\right)$ 和平均数 $(\bar{x})$ 必定相等，即 $M_o=M_e=\bar{x}$ ；如果数据是左偏分布，说明数据存在极小值，必然拉动平均数向极小值一方靠，而众数和中位数由于是位置代表值，不受极值的影响，因此三者之间的关系表现为： $\bar{x}<M_e<M_o$ ；如果数据是右偏分布，说明数据存在极大值，必然拉动平均数向极大值一方靠，因此 $M_o<M_e<\bar{x}$ 。

掌握众数，中位数和平均数的特点，有助于在实际应用中选择合理的测度值来描述数据的集中趋势。

众数是一组数据分布的峰值，不受极端值的影响。其缺点是具有不唯一性，一组数据可能有一个众数，也可能有两个或多个众数，还可能没有众数。众数只有在数据量较多时才有意义，当数据量较少时，不宜使用众数。众数适合作为分类数据的集中趋势测度值。

中位数是一组数据中间位置上的值，不受数据极端值的影响。当一组数据的分布偏斜程度较大时，使用中位数也许是一个不错的选择。中位数适合作为顺序数据的集中趋势测度值。

平均数是针对数值数据计算的，而且利用了全部数据信息，它是应用最广泛的集中趋势测度值。当数据呈对称分布或接近对称分布时，三个代表值相等或接近相等，这时应选择平均数作为集中趋势的代表值。平均数的主要缺点是易受数据极端值的影响，对于偏态分布的数据，平均数的代表性较差。因此，当数据为偏态分布，特别是偏斜程度较大时，可以考虑选择中位数或众数，这时它们的代表性要比平均数好。