7._全距_四分位距_方差_标准差 - 概率论与数理统计

描述样本数据离散程度的统计量主要有全距，四分位距，方差，标准差以及测度相对离散程度的离散系数等。

全距和四分位距

全距

全距（range）是一组数据的最大值与最小值之差，也称极差，用 $R$ 表示。计算公式为：

R=\max (x)-\min (x)

下表显示30个人每月网购数据。 $图片$

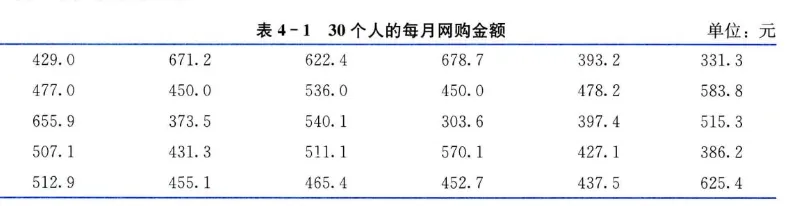
例如，根据例 4.1 中的数据，计算 30 个消费者每月网购金额的全距为： $R=678.7-$ $303.6=375.1$ 。由于全距只是利用了一组数据两端的信息，容易受极端值的影响，不能全面反映数据的差异状况。虽然全距在实际中很少单独使用，但它总是作为分析数据离散程度的一个参考值。

四分位距

四分位距（inter－quartile range）是一组数据 $75 \%$ 位置上的四分位数与 $25 \%$ 位置上的四分位数之差，也称四分位差，用 $I Q R$ 表示。计算公式为：

I Q R=Q_{75 \%}-Q_{25 \%}

四分位距反映了中间 $50 \%$ 数据的离散程度：其数值越小，说明中间的数据越集中，数值越大，说明中间的数据越分散。四分位距不受极值的影响。此外，由于中位数处于数据的中间位置，因此，四分位距的大小在一定程度上也说明了中位数对一组数据的代表程度。例如，根据例 4.1 计算的 30 个消费者每月网购金额的四分位数， $I Q R=547.6-$ $428.525=119.075$ 。

方差和标准差

如果考虑每个数据 $x_i$ 与其平均数 $\bar{x}$ 之间的差异，以此作为一组数据离散程度的度量，结果就要比全距和四分位距更为全面和准确。这就需要求出每个数据 $x_i$ 与其平均数 $\bar{x}$ 离差的平均数。但由于 $\left(x_i-\bar{x}\right)$ 之和等于 0 ，需要进行一定的处理。一种方法是将离差取绝对值，求和后再平均，这一结果称为平均差（mean deviation）或称平均绝对离差（mean absolute deviation）；另一种方法是将离差平方后再求平均数，这一结果称为方差（variance）。方差开方后的结果称为标准差（standard deviation）。方差（或标准差）是实际中应用最广泛的测度数据离散程度的统计量。

设样本方差为 $s^2$ ，根据原始数据计算样本方差的公式为：

s^2=\frac{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2}{n-1}

样本标准差的计算公式为：

s=\sqrt{\frac{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2}{n-1}}

如果原始数据被分成 $k$ 组，各组的组中值分别为 $m_1, m_2, \cdots, m_k$ ，各组的频数分别为 $f_1, f_2, \cdots, f_k$ ，则加权样本方差的计算公式为

s^2=\frac{\sum_{i=1}^k\left(m_i-\bar{x}\right)^2 f_i}{n-1}

加权样本标准差的计算公式为：

s=\sqrt{\frac{\sum_{i=1}^k\left(m_i-\bar{x}\right)^2 f_i}{n-1}}

与方差不同的是，标准差具有量纲，它与原始数据的计量单位相同，其实际意义要比方差清楚。因此，在对实际问题进行分析时更多地使用标准差。

沿用例 4．1表。计算 30 个消费者每月网购金额的方差和标准差。－•解根据式（4．11）得：

\begin{aligned} s^2 & =\frac{(429.0-488.95)^2+(671.2-488.95)^2+\cdots+(625.4-488.95)^2}{30-1} \\ & =9529.6812 \end{aligned}

标准差为 $\sqrt{9529.6812}=97.62$ 。

离散系数

标准差是反映数据离散程度的绝对值，其数值的大小受原始数据取值大小的影响，数据的观测值越大，标准差的值通常也就越大。此外，标准差与原始数据的计量单位相同，采用不同计量单位计量的数据，其标准差的值也就不同。因此，对于不同组别的数据，如果原始数据的观测值相差较大或计量单位不同，就不能用标准差直接比较其离散程度，这时需要计算离散系数。

离散系数（coefficient of variation，CV）也称变异系数，它是一组数据的标准差与其相应的平均数之比。由于离散系数消除了数据取值大小和计量单位对标准差的影响，因而可以反映一组数据的相对离散程度。其计算公式为：

C V=\frac{s}{\bar{x}}

离散系数主要用于比较不同样本数据的离散程度。离散系数大说明数据的相对离散程度也大，离散系数小说明数据的相对离散程度也小

例在奥运会女子 10 米气手枪比赛中，每个运动员首先进行每组 10 枪共 4 组的预赛，然后根据预赛总成绩确定进入决赛的 8 名运动员。决赛时 8 名运动员再进行 10 枪射击，将预赛成绩加上决赛成绩来确定最后的名次。在2008年8月10日举行的第29届北京奥运会女子 10 米气手枪决赛中，进入决赛的 8 名运动员的预赛成绩和最后 10 枪的决赛成绩如表 4－5 所示。评价哪名运动员的发挥更稳定。 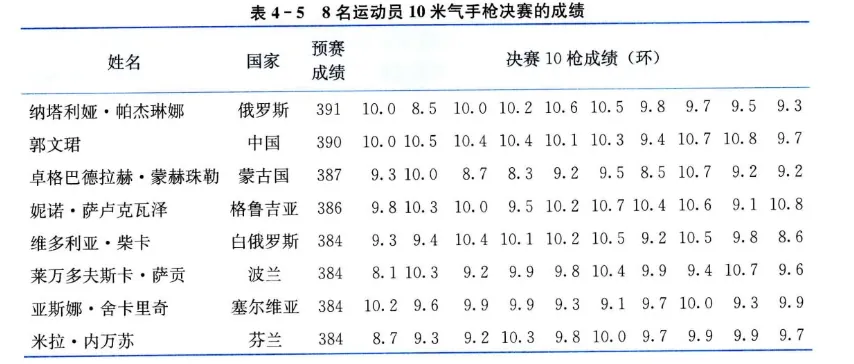$图片$ －•解如果各运动员决赛 10 枪的平均成绩差异不大，可以直接比较标准差的大小，否则需要计算离散系数。8 名运动员最后 10 枪决赛的平均成绩，标准差和离散系数如表4－6所示。 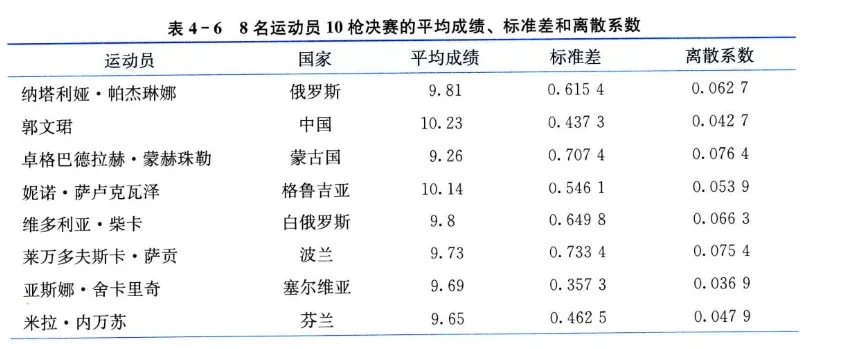$图片$ 从离散系数可以看出，在最后 10 枪的决赛中，发挥比较稳定的运动员是塞尔维亚的亚斯娜•舍卡里奇和中国的郭文珺，发挥不稳定的运动员是蒙古国的卓格巴德拉赫•蒙赫珠勒和波兰的莱万多夫斯卡•萨贡。

标准分数

有了平均数和标准差之后，可以计算一组数据中每个数值的标准分数（standard score）。它是某个数据与其平均数的离差除以标准差后的值。设样本数据的标准分数为 $z$ ，则有：

z_i=\frac{x_i-\bar{x}}{s}

标准分数可以测度每个数值在该组数据中的相对位置，并可以用来判断一组数据是否有离群点。比如，全班的平均考试分数为 80 分，标准差为 10 分，而你的考试分数是 90分，距离平均分数有多远？显然是 1 个标准差的距离。这里的 1 就是你考试成绩的标准分数。标准分数说的是某个数据与平均数相比相差多少个标准差。将一组数据化为标准化得分的过程称为数据的标准化。式（4．16）也就是统计上常用的标准化公式，在对多个具有不同量纲的变量进行处理时，常常需要对各变量的数据进行标准化处理，也就是把一组数据转化成具有平均数为 0 ，标准差为 1 的新的数据。实际上，标准分数只是将原始数据进行了线性变换，它并没有改变某个数值在该组数据中的位置，也没有改变该组数据分布的形状。

例沿用例 4．1。计算 30 个消费者每月网购金额的标准分数。－•解根据上面的计算结果， $\bar{x}=488.95, s=97.62$ 。以第 1 个消费者的标准分数为例，由式（4．16）得：

z=\frac{429.0-488.95}{97.62}=-0.6141

结果表示，第 1 个消费者的每月网购金额比平均每月网购金额低 0.6141 个标准差。