8._偏度系数与峰度系数 - 概率论与数理统计

利用直方图可以看出数据的分布是否对称。对于不对称的分布，要想知道不对称程度则需要计算相应的描述统计量。偏度系数和峰度系数就是对分布不对称程度和峰值高低的一种度量。

偏度系数

偏度（skewness）是指数据分布的不对称性，这一概念由统计学家皮尔逊（K．Pearson）于 1895 年首次提出。测度数据分布不对称性的统计量称为偏度系数（coefficient of skew－ ness），记为 $S K$ 。根据原始数据计算偏度系数时，通常采用下面的公式：

S K=\frac{n}{(n-1)(n-2)} \sum\left(\frac{x_i-\bar{x}}{s}\right)^3

当数据对称分布时，偏度系数等于 0 。偏度系数越接近 0 ，偏斜程度就越低，就越接近对称分布。如果偏度系数明显不等于 0 ，表示分布是非对称的。若偏度系数大于 1 或小于 -1 ，视为严重偏斜分布；若偏度系数在 $0.5 \sim 1$ 或 $-1 \sim-0.5$ 之间，视为中等偏斜分布；偏度系数在 $0 \sim 0.5$ 或 $-0.5 \sim 0$ 之间时，视为轻微偏斜。其中负值表示左偏分布（在分布的左侧有长尾），正值则表示右偏分布（在分布的右侧有长尾）。

峰度系数

峰度（kurtosis）是指数据分布峰值的高低，这一概念由统计学家皮尔逊于 1905 年首次提出。测度一组数据分布峰值高低的统计量称为峰度系数（coefficient of kurtosis），记作 $K$ 。根据原始数据计算峰度系数时，通常采用下面的公式：

K=\frac{n(n+1)}{(n-1)(n-2)(n-3)} \sum\left(\frac{x_i-\bar{x}}{s}\right)^4-\frac{3(n-1)^2}{(n-2)(n-3)}

峰度通常是与标准正态分布相比较而言的。由于标准正态分布的峰度系数为 0 ，当 $K>0$ 时为尖峰分布，数据分布的峰值比标准正态分布高，数据相对集中；当 $K<0$ 时为扁平分布，数据分布的峰值比标准正态分布低，数据相对分散。

下表显示30个人每月网购数据。 $图片$

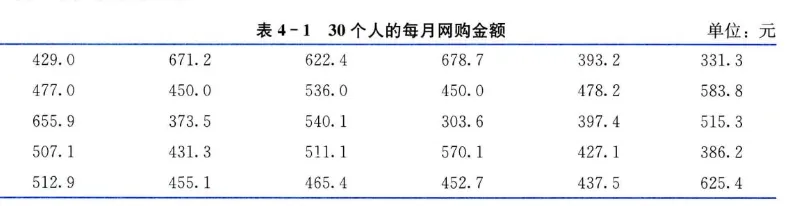
沿用上表。计算 30 个消费者每月网购金额的偏度系数和峰度系数。－解根据式（4．17）得偏度系数为：

\begin{aligned} S K & =\frac{30}{(30-1)(30-2)} \sum\left(\frac{x_i-488.95}{97.62}\right)^3 \\ & =\frac{30}{(30-1)(30-2)} \times 9.217966 \\ & =0.3406 \end{aligned}

结果表示，网购金额为轻微的右偏。根据式（4．18）得峰度系数为：

\begin{aligned} K & =\frac{30 \times(30+1)}{(30-1)(30-2)(30-3)} \sum\left(\frac{x_i-488.95}{97.62}\right)^4-\frac{3 \times(30-1)^2}{(30-2)(30-3)} \\ & =-0.4075 \end{aligned}