19._阅读_正态分布的密度函数是如何推导出来

正态分布的密度函数是如何得来的

正态分布是一种常见的分布，他的密度函数是

f(x)=12πσe−12(x−μσ)2f(x)=\dfrac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2}

这个公式是德国数学家高斯推出来的，因此正态分布也被称作高斯分布

图片{width=200px}

关于高斯的介绍请点击 此处

正态分布如此重要，以至于原德国货币10马克上，直接把高斯、正态分布曲线及其公式都画上去了，这可见高斯和正态分布在数理统计中的重要地位。

图片{width=500px}

根据当年高斯发表的《天体运行论》(Theoria Motus Corporum Coelestium in Sectionibus Conicis Solem Ambientium, 1809)，沿寻着高斯的思路进行推导。

推导

假设有误差概率密度函数 f(t)f(t) ，现在有 nn 个独立观测的值 x1,x2,⋯xnx_1, x_2, \cdots x_n ，假设真值为 μ\mu ，那么误差为：

ε1=x1−με2=x2−μ⋮εn=xn−μ\begin{aligned} \varepsilon_1 & =x_1-\mu \\ \varepsilon_2 & =x_2-\mu \\ & \vdots \\ \varepsilon_n & =x_n-\mu \end{aligned}

根据生活经验，这个误差 ε\varepsilon ，在做大量的观测下，其大部分的数值应在 0 附近范围波动，且出现的频数较多。而误差大的观测值，相应的 ∣ε∣|\varepsilon| 也应很大，出现的频数也应该较小。做极大似然函数 ：

L(μ)=∏i=1nf(εi)=f(x1−μ)f(x2−μ)⋯f(xn−μ)\begin{aligned} L(\mu) & =\prod_{i=1}^n f\left(\varepsilon_i\right) \\ & =f\left(x_1-\mu\right) f\left(x_2-\mu\right) \cdots f\left(x_n-\mu\right) \end{aligned}

对 L(μ)L(\mu) 取自然对数：

ln⁡[L(μ)]=ln⁡[∏i=1nf(εi)]=ln⁡[f(x1−μ)f(x2−μ)⋯f(xn−μ)]=ln⁡[f(x1−μ)]+ln⁡[f(x2−μ)]+⋯+ln⁡[f(xn−μ)]=∑i=1nln⁡[f(xi−μ)]\begin{aligned} \ln [L(\mu)] & =\ln \left[\prod_{i=1}^n f\left(\varepsilon_i\right)\right] \\ & =\ln \left[f\left(x_1-\mu\right) f\left(x_2-\mu\right) \cdots f\left(x_n-\mu\right)\right] \\ & =\ln \left[f\left(x_1-\mu\right)\right]+\ln \left[f\left(x_2-\mu\right)\right]+\cdots+\ln \left[f\left(x_n-\mu\right)\right] \\ & =\sum_{i=1}^n \ln \left[f\left(x_i-\mu\right)\right] \end{aligned}

为了得到 L(μ)L(\mu) 的最大值，对其 ln⁡[L(μ)]\ln [L(\mu)] 求偏导并令其等于 0 ：

∂ln⁡[L(μ)]∂μ=∂∑i=1nln⁡[f(xi−μ)]∂μ=−∑i=1nf′(xi−μ)f(xi−μ)=0\begin{aligned} \frac{\partial \ln [L(\mu)]}{\partial \mu} & =\frac{\partial \sum_{i=1}^n \ln \left[f\left(x_i-\mu\right)\right]}{\partial \mu} \\ & =-\sum_{i=1}^n \frac{f^{\prime}\left(x_i-\mu\right)}{f\left(x_i-\mu\right)} \\ & =0 \end{aligned}

注意上面出现的负号一； 令 g(t)=f′(t)f(t)g(t)=\frac{f^{\prime}(t)}{f(t)} ，则上述式子变成：

∑i=1ng(xi−μ)=0\sum_{i=1}^n g\left(x_i-\mu\right)=0

到了这一步后，精彩的部分就开始来了，这也是高斯的高明之处，他认为 μ\mu 的无偏估计应为 xˉ(xi\bar{x}\left(x_i\right. 的算术平均数）。如果有学过概率论与数理统计，应该知道，根据大数定律 ，当观测值 (x1,x2,⋯xn)\left(x_1, x_2, \cdots x_n\right) 的个数非常大的时候 (n→∞),xˉ(n \rightarrow \infty), \bar{x} 应该是无限接近 μ\mu 。那么，把上面的 ∑\sum 式里 μ\mu 用 xˉ\bar{x} 来代替，则原式子变为：

∑i=1ng(xi−xˉ)=0\sum_{i=1}^n g\left(x_i-\bar{x}\right)=0

其中，

xˉ=1n∑i=1nxi\bar{x}=\frac{1}{n} \sum_{i=1}^n x_i

解上述方程，对每个 xix_i 求偏导，比如对 x1x_1 求偏导，可得如下方程：

∂∑i=1ng(xi−xˉ)∂x1=∂∑i=1ng(xi−1n∑i=1nxi)∂x1=g′(x1−xˉ)(1−1n)+g′(x2−xˉ)(−1n)+⋯+g′(xn−xˉ)(−1n)=0\begin{aligned} \frac{\partial \sum_{i=1}^n g\left(x_i-\bar{x}\right)}{\partial x_1} & =\frac{\partial \sum_{i=1}^n g\left(x_i-\frac{1}{n} \sum_{i=1}^n x_i\right)}{\partial x_1} \\ & =g^{\prime}\left(x_1-\bar{x}\right)\left(1-\frac{1}{n}\right)+g^{\prime}\left(x_2-\bar{x}\right)\left(-\frac{1}{n}\right)+\cdots+g^{\prime}\left(x_n-\bar{x}\right)\left(-\frac{1}{n}\right) \\ & =0 \end{aligned}

注意，上述式子中， xˉ\bar{x} 为 x1x_1 的函数，所以根据复合函数求导法则，得出上述式子。和 x1x_1类似，依次得出 x1x_1 和其他 xix_i 的表达式，可得如下方程组：

g′(x1−xˉ)(1−1n)+g′(x2−xˉ)(−1n)+⋯+g′(xn−xˉ)(−1n)=0g′(x1−xˉ)(−1n)+g′(x2−xˉ)(1−1n)+⋯+g′(xn−xˉ)(−1n)=0⋮g′(x1−xˉ)(−1n)+g′(x2−xˉ)(−1n)+⋯+g′(xn−xˉ)(1−1n)=0\begin{gathered} g^{\prime}\left(x_1-\bar{x}\right)\left(1-\frac{1}{n}\right)+g^{\prime}\left(x_2-\bar{x}\right)\left(-\frac{1}{n}\right)+\cdots+g^{\prime}\left(x_n-\bar{x}\right)\left(-\frac{1}{n}\right)=0 \\ g^{\prime}\left(x_1-\bar{x}\right)\left(-\frac{1}{n}\right)+g^{\prime}\left(x_2-\bar{x}\right)\left(1-\frac{1}{n}\right)+\cdots+g^{\prime}\left(x_n-\bar{x}\right)\left(-\frac{1}{n}\right)=0 \\ \vdots \\ g^{\prime}\left(x_1-\bar{x}\right)\left(-\frac{1}{n}\right)+g^{\prime}\left(x_2-\bar{x}\right)\left(-\frac{1}{n}\right)+\cdots+g^{\prime}\left(x_n-\bar{x}\right)\left(1-\frac{1}{n}\right)=0 \end{gathered}

将 g′(xi−xˉ)g^{\prime}\left(x_i-\bar{x}\right) 看做未知数，把上述 nn 个齐次线性方程组写成矩阵方程 Ax=0A x = 0 的形式：

(1−1n−1n⋯−1n−1n1−1n⋯−1n⋮⋮⋮⋮−1n−1n−1n1−1n)(g′(x1−xˉ)g′(x2−xˉ)⋮g′(xn−xˉ))=(00⋮0)\left(\begin{array}{cccc} 1-\frac{1}{n} & -\frac{1}{n} & \cdots & -\frac{1}{n} \\ -\frac{1}{n} & 1-\frac{1}{n} & \cdots & -\frac{1}{n} \\ \vdots & \vdots & \vdots & \vdots \\ -\frac{1}{n} & -\frac{1}{n} & -\frac{1}{n} & 1-\frac{1}{n} \end{array}\right)\left(\begin{array}{c} g^{\prime}\left(x_1-\bar{x}\right) \\ g^{\prime}\left(x_2-\bar{x}\right) \\ \vdots \\ g^{\prime}\left(x_n-\bar{x}\right) \end{array}\right)=\left(\begin{array}{c} 0 \\ 0 \\ \vdots \\ 0 \end{array}\right)

解到这一步，还真的得回去翻高等代数的教材。这个方程的解并不是那么的容易。很多＂容易看出＂、＂显然＂，对我来说，真的不是那么＂容易看出＂和＂显然＂的。

对于上述方程组的系数矩阵 MM ，将第 2⋯n2 \cdots n 行依次加到第 1 行，可得如下矩阵：

M=(1−1n−1n⋯−1n−1n1−1n⋯−1n⋮⋮⋮⋮−1n−1n−1n1−1n)→(00⋯0−1n1−1n⋯−1n⋮⋮⋮⋮−1n−1n−1n1−1n)M =\left(\begin{array}{cccc} 1-\frac{1}{n} & -\frac{1}{n} & \cdots & -\frac{1}{n} \\ -\frac{1}{n} & 1-\frac{1}{n} & \cdots & -\frac{1}{n} \\ \vdots & \vdots & \vdots & \vdots \\ -\frac{1}{n} & -\frac{1}{n} & -\frac{1}{n} & 1-\frac{1}{n} \end{array}\right) \rightarrow\left(\begin{array}{cccc} 0 & 0 & \cdots & 0 \\ -\frac{1}{n} & 1-\frac{1}{n} & \cdots & -\frac{1}{n} \\ \vdots & \vdots & \vdots & \vdots \\ -\frac{1}{n} & -\frac{1}{n} & -\frac{1}{n} & 1-\frac{1}{n} \end{array}\right)

第一行全为 0 ，那么 det⁡(M)=0\operatorname{det}( M )=0 ，这只能说明方程组有无穷多解，具体还要算出 rank⁡(M)\operatorname{rank}( M ) ，那么就要算出 MM 内子式阶数小于 nn 的行列式的值。按如下分析：

系数矩阵可以写成如下形式：

M=(1−1n−1n⋯−1n−1n1−1n⋯−1n⋮⋮⋮⋮−1n−1n−1n1−1n)=(11⋱1)−(1n1n⋯1n1n1n⋯1n⋮⋮⋮⋮1n1n1n1n)=(11⋱1)−(11⋮1)(1n1n⋯1n)=In−αβT\begin{aligned} M & =\left(\begin{array}{cccc} 1-\frac{1}{n} & -\frac{1}{n} & \cdots & -\frac{1}{n} \\ -\frac{1}{n} & 1-\frac{1}{n} & \cdots & -\frac{1}{n} \\ \vdots & \vdots & \vdots & \vdots \\ -\frac{1}{n} & -\frac{1}{n} & -\frac{1}{n} & 1-\frac{1}{n} \end{array}\right) \\ & =\left(\begin{array}{cccc} 1 & & & \\ & 1 & & \\ & & \ddots & \\ & & & 1 \end{array}\right)-\left(\begin{array}{cccc} \frac{1}{n} & \frac{1}{n} & \cdots & \frac{1}{n} \\ \frac{1}{n} & \frac{1}{n} & \cdots & \frac{1}{n} \\ \vdots & \vdots & \vdots & \vdots \\ \frac{1}{n} & \frac{1}{n} & \frac{1}{n} & \frac{1}{n} \end{array}\right) \\ & =\left(\begin{array}{cccc} 1 & & & \\ & 1 & & \\ & & \ddots & \\ & & & 1 \end{array}\right)-\left(\begin{array}{c} 1 \\ 1 \\ \vdots \\ 1 \end{array}\right)\left(\begin{array}{cccc} \frac{1}{n} & \frac{1}{n} & \cdots & \frac{1}{n} \end{array}\right) \\ & = I _n- \alpha \beta ^{T} \end{aligned}

根据《高等代数》 （第四版，谢启鸿，姚慕生，复旦大学出版社）里面的定理： AA 为 m×nm \times n 矩阵， BB 为 n×mn \times m 矩阵 (m>n)(m>n) ，则存在等式：

∣λIm−AB∣=λm−n∣λIn−BA∣\left|\lambda I _{ m }- A B \right|=\lambda^{m-n}\left|\lambda I _n- B A \right|

根据上述定理，令 A=α,B=β,λ=1A = \alpha , B = \beta , \lambda=1 ，则：

∣M∣=∣In−αβT∣=∣I1−βTα∣=∣ 111n⋯1n)(11⋮1)∣ =∣1−1∣=0\begin{aligned} | M | & =\left| I _n- \alpha \beta ^{T}\right|=\left| I _{ 1 }- \beta ^{T} \alpha \right| \\ & \left.=\left\lvert\, \begin{array}{llll} 1 & & \\ 1 & \frac{1}{n} & \cdots & \frac{1}{n} \end{array}\right.\right) \left.\left(\begin{array}{c} 1 \\ 1 \\ \vdots \\ 1 \end{array}\right) \right\rvert\, \\ & =|1-1| \\ & =0 \end{aligned}

而对于 MM 的前 n−1n-1 阶主子式 NN ，形式类似，也可以拆解成如下形式，但是只有 n−1n-1阶：

N=(1−1n−1n⋯−1n−1n1−1n⋯−1n⋮⋮⋮⋮−1n−1n−1n1−1n)(n−1)×(n−1)=(11⋱1)−(1n1n⋯1n1n1n⋯1n⋮⋮⋮⋮1n1n1n1n)=(11⋱1)−(11⋮1)(1n1n⋯1n)=In−1−γηT\begin{aligned} N & =\left(\begin{array}{cccc} 1-\frac{1}{n} & -\frac{1}{n} & \cdots & -\frac{1}{n} \\ -\frac{1}{n} & 1-\frac{1}{n} & \cdots & -\frac{1}{n} \\ \vdots & \vdots & \vdots & \vdots \\ -\frac{1}{n} & -\frac{1}{n} & -\frac{1}{n} & 1-\frac{1}{n} \end{array}\right)_{(n-1) \times(n-1)} \\ & =\left(\begin{array}{cccc} 1 & & & \\ & 1 & & \\ & & \ddots & \\ & & & 1 \end{array}\right)-\left(\begin{array}{cccc} \frac{1}{n} & \frac{1}{n} & \cdots & \frac{1}{n} \\ \frac{1}{n} & \frac{1}{n} & \cdots & \frac{1}{n} \\ \vdots & \vdots & \vdots & \vdots \\ \frac{1}{n} & \frac{1}{n} & \frac{1}{n} & \frac{1}{n} \end{array}\right) \\ & =\left(\begin{array}{cccc} 1 & & & \\ & 1 & & \\ & & \ddots & \\ & & & 1 \end{array}\right)-\left(\begin{array}{c} 1 \\ 1 \\ \vdots \\ 1 \end{array}\right)\left(\begin{array}{cccc} \frac{1}{n} & \frac{1}{n} & \cdots & \left.\frac{1}{n}\right) \end{array}\right. \\ & = I _{n-1}- \gamma \eta ^{T} \end{aligned}

那么

∣N∣=∣In−1−γηT∣=∣I1−ηTγ∣=∣1−(1n1n⋯1n)1×(n−1)(11⋮1)(n−1)×1∣=∣1−n−1n∣=1n≠0\begin{aligned} | N | & =\left| I _{n- 1 }- \gamma \eta ^{T}\right|=\left| I _{ 1 }- \eta ^{T} \gamma \right| \\ & =\left|1-\left(\begin{array}{llll} \frac{1}{n} & \frac{1}{n} & \cdots & \frac{1}{n} \end{array}\right)_{1 \times(n-1)}\left(\begin{array}{c} 1 \\ 1 \\ \vdots \\ 1 \end{array}\right)_{(n-1) \times 1}\right| \\ & =\left|1-\frac{n-1}{n}\right| \\ & =\frac{1}{n} \neq 0 \end{aligned}

所以 rank⁡(M)=n−1\operatorname{rank}( M )=n-1 ，所以线性方程组的自由变量的个数：

n−rank⁡(M)=n−(n−1)=1n-\operatorname{rank}( M )=n-(n-1)=1

因而，上述方程组的解可写成：

X=k(g′(x1−xˉ)g′(x2−xˉ)⋮g′(xn−xˉ))=k(11⋮1)X =k\left(\begin{array}{c} g^{\prime}\left(x_1-\bar{x}\right) \\ g^{\prime}\left(x_2-\bar{x}\right) \\ \vdots \\ g^{\prime}\left(x_n-\bar{x}\right) \end{array}\right)=k\left(\begin{array}{c} 1 \\ 1 \\ \vdots \\ 1 \end{array}\right)

即 g′(x1−xˉ)=g′(x2−xˉ)=⋯=g′(xn−xˉ)=kg^{\prime}\left(x_1-\bar{x}\right)=g^{\prime}\left(x_2-\bar{x}\right)=\cdots=g^{\prime}\left(x_n-\bar{x}\right)=k ，解微分方程，可得：

g(t)=kt+bg(t)=k t+b

因为 ∑i=1ng(xi−xˉ)=0\sum_{i=1}^n g\left(x_i-\bar{x}\right)=0 ，将 g(t)=kt+bg(t)=k t+b 带入该式，可得：

∑i=1n[k(xi−xˉ)+b]=0⇔k∑i=1n(xi−xˉ)+nb=0⇔k(∑i=1nxi−nxˉ)+nb=0⇔nb=0⇔b=0\begin{aligned} \sum_{i=1}^n\left[k\left(x_i-\bar{x}\right)+b\right]=0 & \Leftrightarrow k \sum_{i=1}^n\left(x_i-\bar{x}\right)+n b=0 \\ & \Leftrightarrow k\left(\sum_{i=1}^n x_i-n \bar{x}\right)+n b=0 \\ & \Leftrightarrow n b=0 \\ & \Leftrightarrow b=0 \end{aligned}

求得 g(t)=ktg(t)=k t ，即 f′(t)f(t)=kt\frac{f^{\prime}(t)}{f(t)}=k t ，求解该微分方程：

∫f′(t)f(t)dt=∫ktdt⇔∫d[f(t)]f(t)=12kt2+c⇔ln⁡[f(t)]=12kt2+c⇔f(t)=Ke12kt2\begin{aligned} \int \frac{f^{\prime}(t)}{f(t)} d t=\int k t d t & \Leftrightarrow \int \frac{d[f(t)]}{f(t)}=\frac{1}{2} k t^2+c \\ & \Leftrightarrow \ln [f(t)]=\frac{1}{2} k t^2+c \\ & \Leftrightarrow f(t)=K e^{\frac{1}{2} k t^2} \end{aligned}

同时，f(t)f(t) 为概率密度函数，那么其从 −∞-\infty 到 +∞+\infty 的积分为 1 （概率密度的正则性），则

∫−∞+∞f(t)dt=1\int_{-\infty}^{+\infty} f(t) d t=1

其中，f(t)=Ke12kt2f(t)=K e ^{\frac{1}{2} k t^2} ，为保证积分收玫，则 k<0k<0 ，令

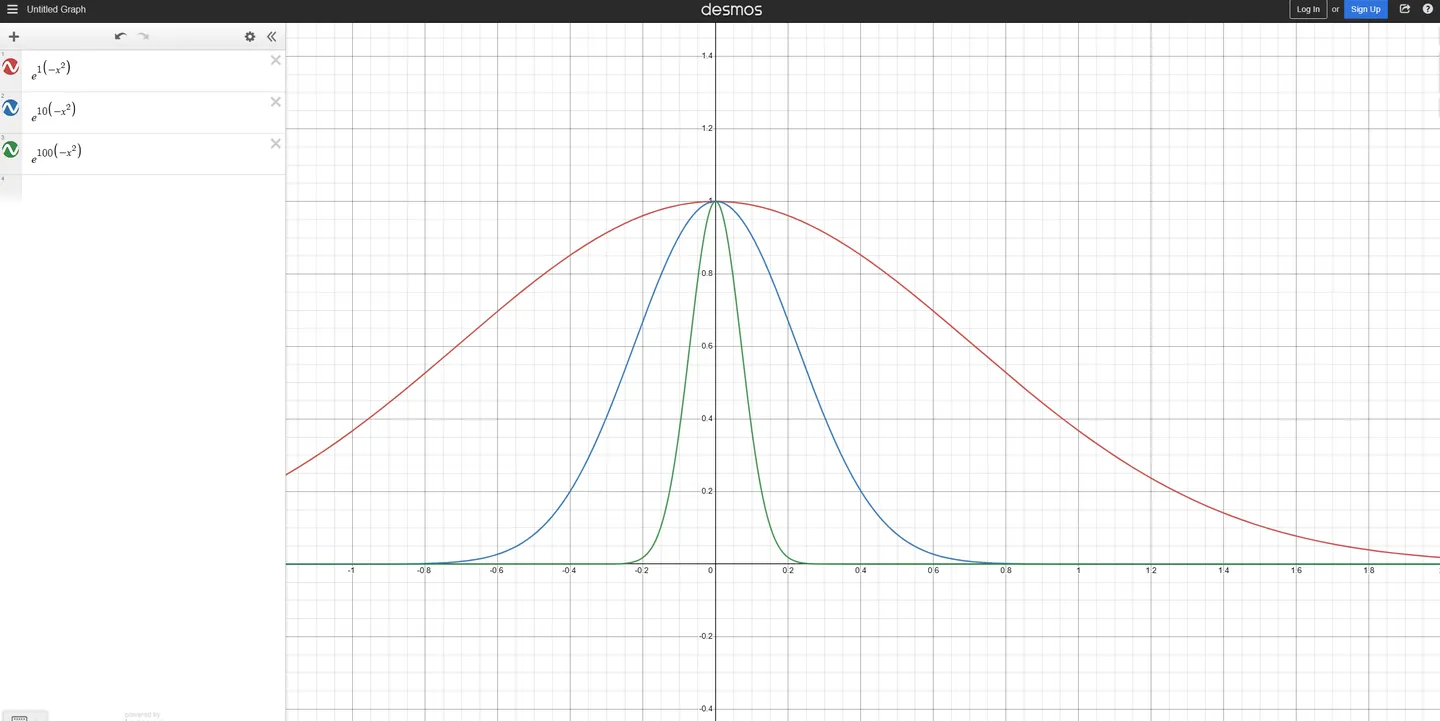
k=−1σ2<0k=-\frac{1}{\sigma^2}<0

这一步真不知道高斯是怎么想的。既能能保证 k<0k<0 ，同时引入了方差 σ2\sigma^2 ，非常巧妙。盲猜和 e−x2e ^{-x^2} 的形态有关。该函数为偶函数，如图，随 −x2-x^2 前面的系数的增大，函数图像形态越＂尖＂，分布越集中。与我们所知的＂方差越大，越分散；方差越小，越集中＂有些相似，因而将 σ2\sigma^2 引入 −x2-x^2 的系数的分母中，可实现函数图像和实际概率密度函数图像的大致吻合。

图片

求积分：

∫−∞+∞f(t)dt=∫−∞+∞Ke12kt2dt=K∫−∞+∞e−t22σ2dt=K2σ[∫−∞+∞e−(t2σ)2d(12σt)][2σ∫−∞+∞e−(s2σ)2d(12σs)=K2σ∫−∞+∞∫−∞+∞e−(u2+v2)dudv=K2σ∫02πdθ∫0+∞e−r2rdr=K2σπ=1\begin{aligned} \int_{-\infty}^{+\infty} f(t) d t & =\int_{-\infty}^{+\infty} K e^{\frac{1}{2} k t^2} d t \\ & =K \int_{-\infty}^{+\infty} e^{-\frac{t^2}{2 \sigma^2} d t} \\ & =K \sqrt{\sqrt{2} \sigma\left[\int_{-\infty}^{+\infty} e^{-\left(\frac{t}{\sqrt{2} \sigma}\right)^2} d\left(\frac{1}{\sqrt{2} \sigma} t\right)\right]\left[\sqrt{2} \sigma \int_{-\infty}^{+\infty} e^{-\left(\frac{s}{\sqrt{2} \sigma}\right)^2} d\left(\frac{1}{\sqrt{2} \sigma} s\right)\right.} \\ & =K \sqrt{2} \sigma \sqrt{\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} e^{-\left(u^2+v^2\right)} d u d v} \\ & =K \sqrt{2} \sigma \sqrt{\int_0^{2 \pi} d \theta \int_0^{+\infty} e^{-r^2} r d r} \\ & =K \sqrt{2} \sigma \sqrt{\pi} \\ & =1 \end{aligned}

解得 K=12πσK=\frac{1}{\sqrt{2 \pi} \sigma}

最终求得正态分布的概率密度函数

f(t)=12πσe−12(tσ)2\boxed{ f(t)=\dfrac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{1}{2}\left(\dfrac{t}{\sigma}\right)^2} }

本文转摘知乎不小心把你丢了的文章，点击 此处 查看原文

前の章18._正态分布表的使用与上a分位数-Part4
次の章20._连续型_伽马分布garmma
19._阅读_正态分布的密度函数是如何推导出来 - 概率论与数理统计 | OpenTech