9._矩阵乘法的意义_物理理解

从氢原子能量说起

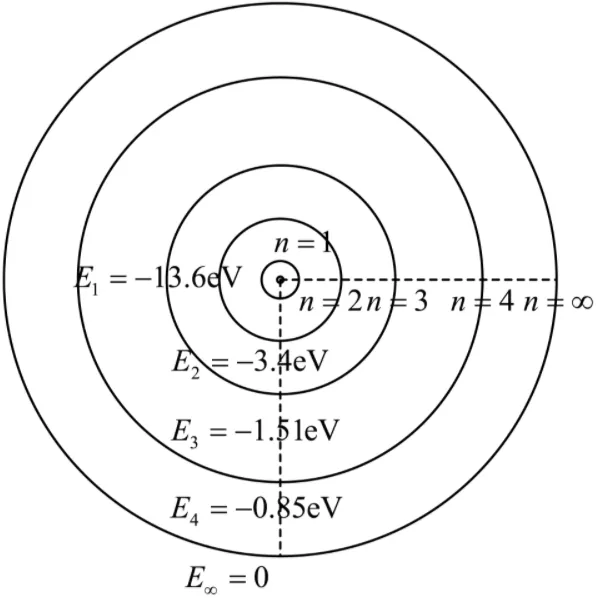
在高中，我们学过，原子中的电子绕着某些特定的轨道以一定的频率运行，并时不时地从一个轨道跃迁到另一个轨道上去。每个电子轨道都代表一个特定的能级，因此当这种跃迁发生的时候，电子就按照量子化的方式吸收或者发射能量，其大小等于两个轨道之间的能量差。 玻尔模型的建立有着氢原子光谱的支持,每一条光谱线都有一种特定的频率，而由量子公式 $E_1-E_2 = hν$，我们知道这是电子在两个能级之间跃迁的结果，那么如何理解这个能量差？而不是“能级”和“轨道”。详见高中物理 原子能级 {width=300px}

公交车收费

为了说明上面的问题, 我们还是来打个比方。小时候的乐趣之一是收集各种各样的电车票以扮作售票员, 那时候上海的车票通常都很便宜, 最多也就是一毛几分钱。但规矩是这样的：不管你从哪个站上车，坐得越远车票就相对越贵。比如我从徐家汇上车, 那么坐到淮海路可能只要 3 分钱, 而到人民广场大概就要 5 分, 到外滩就要 7 分, 如果一直坐到虹口体育场, 也许就得花上 1 毛钱。

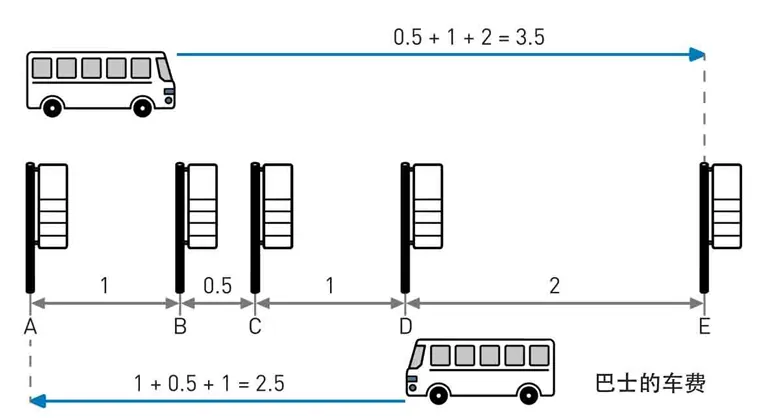
我们假设有一班巴士从 A 站出发, 经过 BCD 三站到达 E 这个终点站。这个车的收费沿用了我们怀旧时代的老传统, 不是上车一律给 2 块钱, 而是根据起点和终点来单独计费。我们不妨订一个收费标准: $A$ 站和 B 站之间是 1 块钱, B 和 C 靠得比较近, 0.5 元。 C 和 D 之间还是 1 块钱, 而 D 和 E 离得远, 2 块钱。这样一来车费就容易计算了, 比如我从 B 站上车到 E 站, 那么我就应该给 $0.5+1+2=3.5$ 元作为车费。反过来,如果我从 D 站上车到 $A$ 站, 那么道理是一样的: $1+0.5+1=2.5$ 块钱。

{width=600px}

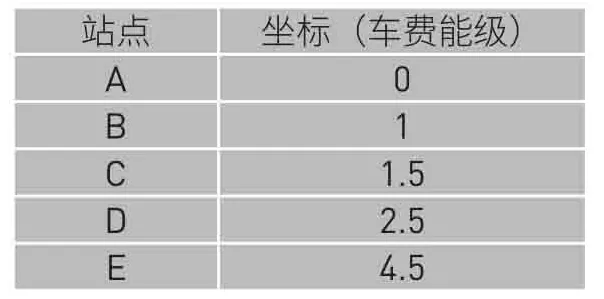
现在要做一个计费系统：这个问题很简单，车费问题实际上就是两个站之间的距离问题, 我们只要把每一个站的位置状况写出来, 那么乘客们就能够一目了然了。于是假设, $A$ 站的坐标是 0 , 从而推出: $B$ 站的坐标是 $1, \mathrm{C}$ 站的坐标是 $1.5, \mathrm{D}$ 站的坐标是 2.5 , 而 E 站的坐标是 4.5 。 这就行了,车费就是起点站的坐标减掉终点站的坐标的绝对值, 我们的"坐标", 实际上可以看成一种 "车费能级", 所有的情况都完全可以包含在下面这个表格里:

{width=400px}

这便是一种经典的解法, 每一个车站都被假设具有某种绝对的"车费能级", 就像原子中电子的每个轨道都被假设具有某种特定的能级一样。所有的车费, 不管是从哪个站到哪个站, 都可以用这个单一的变量来解决, 这是一个一维的传统表格, 完全可以表达为一个普通的公式。这也是所有物理问题的传统解法。

上述思路的问题

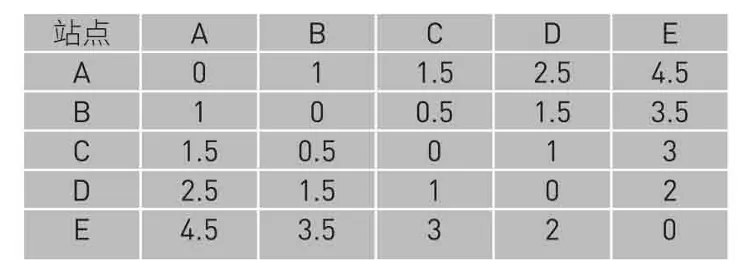
上述思路有一个根本性的错误, 那就是, 作为一个乘客来说, 他完全无法意识, 也根本不可能观察到某个车站的"绝对坐标"是什么。比如我从 C 站乘车到 D 站, 无论怎么样我也无法观察到 " C 站的坐标是 1.5 ", 或者 " D 站的坐标是 2.5 "这个结论。 作为我一一乘客来说, 我所能唯一观察和体会到的, 就是 "从 C 站到达 D 站要花 1 块钱", 这才是最确丵、最坚实的东西。我们的车费规则, 只能以这样的事实为基础，而不是不可观察的所谓"坐标",或者"能级"。 那么, 怎样才能仅仅从这些可以观察的事实上去建立我们的车费规则呢? 传统的那个一维表格已经不适用了, 我们需要一种新类型的表格,像下面这样的:

{width=500px}

这里面, 横坐标是起点站, 纵坐标是终点站。现在这张表格里的每一个数字都是实实在在可以观测和检验的了。比如第一行第三列的那个 1.5 , 它的横坐标是 A, 表明从 A 站出发。它的纵坐标是 C, 表明到 C 站下车。那么, 只要某个乘客真正从 A 站坐到了 C 站, 他就可以证实这个数字是正确的: 这个旅途的确需要 1.5 块车费。 上面的表格， 它没有做任何假设和推论, 不包含任何不可观察的数据。但作为代价，它采纳了一种二维的庞大结构，每个数据都要用横坐标和坚坐标两个变量来表示。正如我们不能用 $v_{x,}$ 而必须用 $v_{x, y}$ 来表示电子频率一样。更关键的是, 所有的物理规则, 也要按照这种表格的方式来改写。我们已经有了经典的动力学方程，现在，我们必须全部把它们按照量子的方式改写成某种表格方程。许多传统的物理变量，现在都要看成是一些独立的矩阵来处理。

但是难题来了, 我们现在有一个变量 $p$, 代表电子的动量; 还有一个变量 $q$, 代表电子的位置。本来, 这是两个经典变量, 我们应该把它们相乘, 大家都没有对此表示任何疑问。可现在，把它们改成了矩阵的表格形式, 这就给我们的运算带来了麻烦。 $p$ 和 $q$ 变成了两个 "表格"! 请问, 你如何把两个"表格"乘起来呢?

矩阵的乘法

为了容易理解, 我们举一个小学生水平的数学练习: 乘法运算。只不过这次乘的不是普通的数字, 而是两张表格:I和 II。它们的内容见下:

我们要解决的是 $\mathrm{I} \times \mathrm{II}$ 等于几?

如何计算

大家还记得, 上面说过，每张表格代表了一种车费表, 那么现在我们的 I 和 II 就分别成了两条路线的旅游巴士, 在两个城市之间来往, 只不过收费有所不同而已。我们把它们称为巴士 I 号线和巴士 II 号线。为了再形象化一点, 我们假设这两个城市是隔着罗湖桥比邻的深圳和香港。

这样的话, 我们的表格就有了具体的现实意义。如前面已经说明的那样, 表的横坐标是出发站, 纵坐标是终点站。所以对于巴士 I 号线来说, 在深圳市内游玩需要 1 块车费, 从深圳出发到香港则要 8 块钱。反过来, 从香港出发回深圳要 7 块钱, 而在香港市内观光则需 3 块 。II 号表格里的数字与此类似。

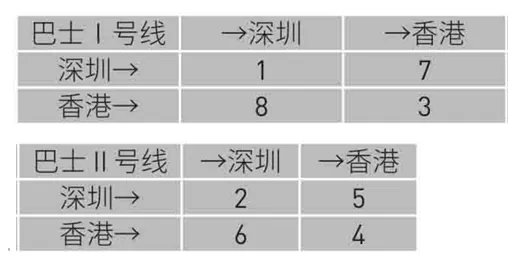
好吧, 到目前为止一切都不错, 可是, 这到底有什么意思呢? $\mathrm{I} \times \mathrm{II}$ 到底是多少呢? 这种运算代表什么意义呢? 和我们的巴土旅游线又有什么关系呢? 暂且不急,让我们一步一步地来解决这个问题。

首先要把握大方向。I 是一个 $2 \times 2$ 的表格, II 也是一个 $2 \times 2$ 的表格。那么, 我们有理由去猜测，它们的乘积应该也是一个 $2 \times 2$ 的表格。

位于左上角的 $a$ 是多少呢? 是不是简单地把 I 号表左上角的 1 乘以 II 号表左上角的 $2,1 \times 2=2$ 就行了呢? 我们要时时牢记车费表的现实意义:左上角代表了从深圳出发, 还在深圳下车的总车费。 $1 \times 2$ 的确符合要求：先乘 I 号线在深圳游玩一阵, 随后原地下车再搭 II 号线再次市内游！总的路线是: 深圳 $\rightarrow$ 深圳 $\rightarrow$ 深圳。起点和终点都在深圳, 坐标在左上角, 没错!

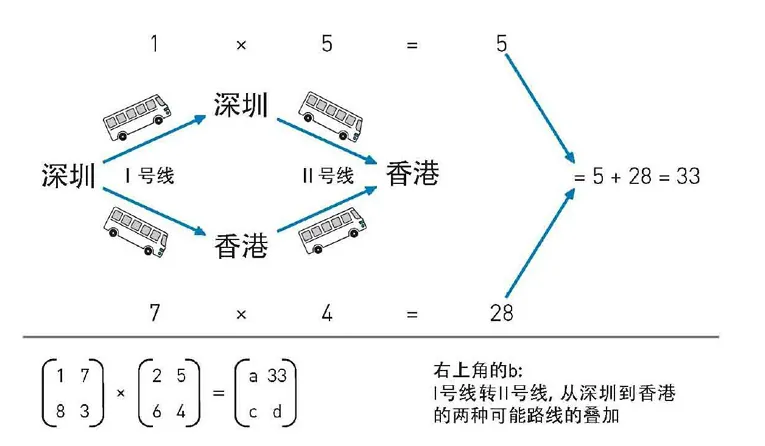
但是, 我们忽略了另一条路线！左上角的 $a$ 要求从深圳出发，最后在深圳下车, 却没有规定整个过程全都在深圳市内! 实际上, 很容易想象另一条路线: 深圳 $\rightarrow$ 香港 $\rightarrow$ 深圳, 它依然符合起点和终点都在深圳的要求。这样一来，我们必须先搭 I 号线去香港（收费 7 元），在香港转搭 II 号线回深圳（收费 6 元），它们的乘积是 $7 \times 6=42$ ！ $a$ 最终的数值, 应该是所有可能路线的叠加（深圳 $\rightarrow ? \rightarrow \rightarrow$ 深圳）。在本例中，只有上述两条路线，没有第三种可能了。所以 $a=1 \times 2+7 \times 6=44$ 。

很奇妙，是不是？我们再来看右上角的 $b$ 。深圳出发香港下车，同样也有两种可能的路线：深圳 $\rightarrow$ 深圳 $\rightarrow$ 香港，或者深圳 $\rightarrow$ 香港 $\rightarrow$ 香港。要么先乘 I 号线深圳市内游再搭 II 号线到香港（ $1 \times 5$ ），要么先乘 I 号线到香港然后转 II 号线香港市内游 $(7 \times 4)$ 。所以综合来说, $b=1 \times 5+7 \times 4=33$ 。

{width=600px}

自己试着求 $c$ 和 $d$ 。最后应该是这样的: $c=8 \times 2+3 \times 6=34, d=8 \times 5+3 \times 4=52$ 。 所以:

很抱歉, 我们处在一个非常奇幻的世界里, 虽然只是小学水平的数字运算, 但是我们必须承认，我们的确学到了一些新的事物,

如果你觉得这种乘法十分陌生的话, 那么我们很快就要给你更大的惊奇, 让我们把上面这道题目的次序倒一倒, 现在验算一遍 II $\times$ I:

我们来看看 $a$ 是什么, 现在我们是先乘搭 II 号线, 然后转 I 号线了。我们可以先搭 II 号线在深圳市内转搭 I 号线再次市内游（深圳 $\rightarrow$ 深圳 $\rightarrow$ 深圳), 对应的是 $2 \times 1$ 。另外, 还有一条路线: 深圳 $\rightarrow$ 香港 $\rightarrow$ 深圳, 所以是先搭 II 号线去香港, 在那里转搭 I 号线回深圳, 所以是 $5 \times 8=40$ 。 所以总的来说, $a=2 \times 1+5 \times 8=42$ 。

我们遇到问题了。在我们的验算里, $a=42$,不过我还记得, 刚才我们的答案说 $a=44$ 。刚才我们的 $a=1 \times 2+7 \times 6=44$ 。 这里的 $a$代表深圳上车深圳下车，所以两种可能的情况是: 深圳 $\rightarrow$ 深圳 $\rightarrow$ 深圳, II 号线市内游收 2 块, I 号线 1 块, 所以 $2 \times 1=2$ 。另外还有深圳 $\rightarrow$ 香港 $\rightarrow$ 深圳的路线。II 号线由深圳去香港 5 块, I 号线由香港回深圳 8 块, 所以 $5 \times 8=40$ 。加在一起: $2+40=42$ !

那么难道前面算错了? 我们再算一遍, 好像也没错,前面 $a=2+42=44$ 。那么, 那么 ……谁错了? 我们似乎发明了一种新的表格乘法, 这种乘法结果: $\mathrm{I} \times \mathrm{II} \neq \mathrm{II} \times \mathrm{I}$ 。 我们不妨把结果整个算出来：

哇, 真的非常不同, 每个数字都不一样, $\mathrm{I} \times \mathrm{II} \neq \mathrm{II} \times \mathrm{II}$ 唉, 这可真让人惋惜。

但是，我们必须学会面对现实。我们已经说过了, 物理学, 必须从唯一可以被实践的数据出发, 而不是靠想象和常识习惯。我们要学会依赖于数学, 而不是日常语言, 因为只有数学才具有唯一的意义, 才能告诉我们唯一的真实。我们必须认识到这一点: 数学怎么说, 我们就得接受什么。如果数学说 I $\times$ II $\neq$ II $\times \mathrm{I}$, 那么我们就得这么认为, 哪怕被嘲笑, 我们也不能改变这一立场。 何况, 如果仔细审查这里面的意义, 也并没有太大的荒谬:

先搭乘 I 号线,再转 II 号线,这和先搭乘 II 号线,再转 I 号线,导致的结果可能是不同的, 有什么问题吗?

注：本文改编自曹天元的《上帝掷骰子吗？》