5._无偏性

评价点估计好不好有三个指标：无偏性是指估计量的期望和总体期望一样。 有效性是指估计量的方差应尽可能小，相合性是指当取样数量无限大时，估计量和真实值应无限接近

点估计好坏的评价标准

对于参数估计，采用不同的评估方法会有不同的结论，比如要估算一个学校里男生的平均身高，可以随机抽查100名学生，计算样本的平均值、中位数、众数、最大值和最小值的平均数、截尾均值等作为总体的平均值，我们希望得到的估计量能体现总体的真实参数，那么在同一参数的多个估计量当中，哪一个是最好的估计量呢？自然需要给出评价估计量优劣的标准，这就是本节介绍的无偏性、有效性和相合性。

注： 截尾均值是指由于均数较易受极端值的影响，因此可以考虑将数据进行行排序后，按照一定比例去掉最两端的数据，只使用中部的数据来求均数这叫做截尾均值

无偏性

题目释义，偏，偏差的意思。 无偏性，就是没有偏差。无偏性就是要求 样本的期望值 等于 总体的期望值。

考虑下面一种情况：为了估算全校男生的平均身高，我们可以对其随机采样，比如我们采样10次，每次采样10人，这样就得到10组数据，

data1:170,168,182,173,174,175,154,172,160,179 data1: 170,168,182,173,174,175,154,172,160,179 算出平均值 X1ˉ=170+168+182+173+174+175+154+172+160+17910=170.7\bar{X_1}=\frac{170+168+182+173+174+175+154+172+160+179}{10}=170.7

data2:161,165,172,173,174,178,179,180,177,179 data2: 161,165,172,173,174,178,179,180,177,179 算出平均值 X2ˉ=161+165+172+173+174+178+179+180+177+17910=173.8\bar{X_2}=\frac{161+165+172+173+174+178+179+180+177+179}{10}=173.8

data3:181,165,172,173,176,173,175,163,162,176 data3: 181,165,172,173,176,173,175,163,162,176 算出平均值 X3ˉ=181+165+172+173+176+173+175+163+162+17610=171.6\bar{X_3}=\frac{181+165+172+173+176+173+175+163+162+176}{10}=171.6 ... 算出10组平均值，得到10组样本均值。（注意：对于每次采样获得的值叫做观测值，一般用xx表示，而算出来的平均值是样本均值，一般用XX表示）

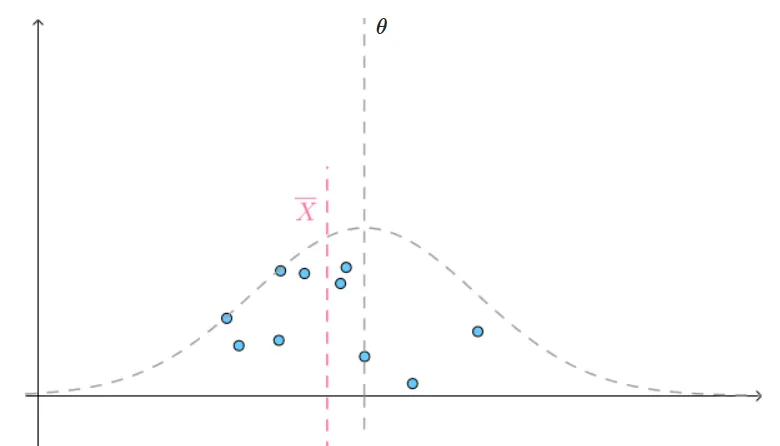
如果设全校男生平均身高的真实值为θ\theta，可以发现每次取样的均值Xˉ\bar{X}都在θ\theta值附近跳动，也许我们永远不知道全校男生的真实值是多少，但是我们可以给出置信区间，比如 95%95 \%把握保证男生的平均身高为 172cm172cm，详见 置信区间

图片{width=500px}

在上面采样里，如果用θ^\hat{\theta} 表示估算的身高，可以看到 θ^\hat{\theta} 是Xˉ\bar{X}的函数，因此，给出如下定义：

定义

估计量 θ^(X1,X2,⋯ ,Xn)\hat{\theta}\left(X_1, X_2, \cdots, X_n\right) 是一个随机变量，对于一次具体的观测结果来说，θ^\hat{\theta}的取值与真实的参数值 θ\theta 一般会有偏差，我们希望 θ^\hat{\theta} 的取值能在 θ\theta 附近波动，而且在多次观测中，θ^\hat{\theta} 的平均值 E(θ^)E(\hat{\theta}) 应与 θ\theta 吻合，由此引出了无偏性的概念．

设 θ^=θ^(X1,X2,⋯ ,Xn)\hat{\theta}=\hat{\theta}\left(X_1, X_2, \cdots, X_n\right) 是未知参数 θ\theta 的估计量，若E(θ^)=θE(\hat{\theta})=\theta 则称 θ^\hat{\theta} 为 θ\theta 的无偏估计量． 如果 lim⁡θ^)=θ\lim \hat{\theta})=\theta 称为渐进无偏估计。

在实际应用中，要求估计量具有无偏性是有实际意义的．例如，在大批商品的交易中，买卖双方一般通过抽样去估计产品的次品率．若估计值高于实际值，将给卖家带来损失．反之，若估计值低于实际值，就会给买家带来损失．但只要采用的估计量是无偏估计量，而且双方的买卖是长期的，则总的来说是互不吃亏的．

无偏性解释

估计量的无偏性有两个含义. 第一个含义是没有系统性的偏差，不论你用什么样的估计量 θ^\hat{\theta} 去估计 θ\theta ，总是时而偏低, 时而偏高. 无偏性表示, 把这些正负偏差在概率上平均起来，其值为 0 。比如您买了一瓶饮料，虽然包装上标准为500ml，但是由于机器问题导致有时候保证超过500ml一点，有时候低于500ml一点，只要再合理范围，我们认为这都是合格的，因此, 无偏估计不等于在任何时候都给出正确无误的估计.

例设 (X1,X2,⋯ ,Xn)\left(X_1, X_2, \cdots, X_n\right) 是来自总体 XX 的一个样本，总体 X∼U(0,θ)X \sim U(0, \theta) 其中 θ>0\theta>0 未知， 试求 （1）θ\theta 的矩估计量 θ^1\hat{\theta}_1 ； （2）θ \theta 的极大似然估计量 θ^2\hat{\theta}_2 ； （3） 问 θ^1,θ^2\hat{\theta}_1, \hat{\theta}_2 是不是未知参数的无偏估计? 若不是，将其修正为无偏估计。

解 (1)由矩估计定义可知 由于 E(X)=θ2E(X)=\frac{\theta}{2} ，则 θ=2E(X)\theta=2 E(X) ，故 θ\theta 的矩估计量 θ^1=2Xˉ\hat{\theta}_1=2 \bar{X}.

(2) 似然函数 L(θ)={1θn,0⩽x1,⋯ ,xn⩽θ0, 其他 L(\theta)=\left\{\begin{array}{ll}\frac{1}{\theta^n}, & 0 \leqslant x_1, \cdots, x_n \leqslant \theta \\ 0, & \text { 其他 }\end{array}\right. ． 因 L(θ)L(\theta) 不可导，可按最大似然法的基本思想确定 θ^\hat{\theta} 。欲使 L(θ)L(\theta) 最大，θ\theta 应尽量小但又不能太小，它必须同时满足 θ⩾xi(i=1,⋯ ,n)\theta \geqslant x_i \quad(i=1, \cdots, n) ，即 θ⩾max⁡(x1,⋯ ,xn)\theta \geqslant \max \left(x_1, \cdots, x_n\right) ，否则 L(θ)=0L(\theta)=0 ，而 0 不可能是 L(θ)L(\theta) 的最大值。因此，当 θ=max⁡{x1,⋯ ,xn}\theta=\max \left\{x_1, \cdots, x_n\right\} 时，L(θ)L(\theta) 可达最大。所以 θ\theta 的最大似然估计为 θ^=max⁡{X1,⋯ ,Xn}\hat{\theta}=\max \left\{X_1, \cdots, X_n\right\} ．

此例说明,当似然函数L(θ)关于θ单调递增(或递减)时,其极值点为θ的最大(或最小)取值点

现在我们分析一下上面两个估计的通俗意义，假设抽查一批钢板厚度服从均匀分布(0,θ)(0,\theta)，抽查的结果是：2.1cm2.4cm2.2cm2.1cm2.3cm2.1cm \quad 2.4cm \quad 2.2cm \quad 2.1cm \quad 2.3cm 其平均值为 Xˉ=(2.1+2.4+2.2+2.1+2.3)/5=2.2cm\bar{X}=(2.1+2.4+2.2+2.1+2.3)/5=2.2cm ,当使用矩估计时，θ=2Xˉ=2.2∗2=4.4\theta=2\bar{X}=2.2 * 2= 4.4 , 而当使用极大似然估计时，θ\theta 为样本里最大值，即θ=2.4\theta=2.4 ，因此一个认为均匀分布是(0,4.4)(0,4.4) , 一个认为均匀分布是(0,2.4)(0,2.4)

(3)

①E(θ^1)=E(2Xˉ)=2E(X)=2×θ2=θE\left(\hat{\theta}_1\right)=E(2 \bar{X})=2 E(X)=2 \times \frac{\theta}{2}=\theta ；

②由次序统计量的分布知当 y∈(0,θ)y \in(0, \theta) 时， X(n)X_{(n)} 的概率密度

函数为

fn(y)=n(yθ)n−1⋅1θ=nyn−1θnf_n(y)=n\left(\frac{y}{\theta}\right)^{n-1} \cdot \frac{1}{\theta}=\frac{n y^{n-1}}{\theta^n}

故 E(θ^2)=E(X(n))=∫0θy⋅nyn−1θndy=nn+1θ\quad E\left(\hat{\theta}_2\right)=E\left(X_{(n)}\right)=\int_0^\theta y \cdot \frac{n y^{n-1}}{\theta^n} d y=\frac{n}{n+1} \theta 因此，矩估计是无偏估计而极大似然估计不是无偏估计。 但是注意到 lim⁡n→+∞E(θ^2)=θ\lim _{n \rightarrow+\infty} E\left(\hat{\theta}_2\right)=\theta ，因此 X(n)X_{( n )} 是 θ\theta 的渐近无偏估计。 定义: θ^2∗=n+1nθ^2=n+1nX(n)\hat{\theta}_2^*=\frac{n+1}{n} \hat{\theta}_2=\frac{n+1}{n} X_{(n)} 则满足 E(θ^2∗)=θE\left(\hat{\theta}_2^*\right)=\theta ，即修正后的 n+1nX(n)\frac{n+1}{n} X_{( n )} 是 θ\theta 的无偏估计。

方差

例 已知 B2=1n∑i=1n(Xi−Xˉ)2B_2=\frac{1}{n} \sum_{i=1}^n\left(X_i-\bar{X}\right)^2 和 S2=1n−1∑i=1n(Xi−Xˉ)2S^2=\frac{1}{n-1} \sum_{i=1}^n\left(X_i-\bar{X}\right)^2 都是总体方差 σ2\sigma^2 的估计量，问：哪个估计量更好？

解 由于

E(S2)=D(X)=σ2E\left(S^2\right)=D(X)=\sigma^2

故样本方差 S2=1n−1∑i=1n(Xi−Xˉ)2S^2=\frac{1}{n-1} \sum_{i=1}^n\left(X_i-\bar{X}\right)^2 是 σ2\sigma^2 的无偏估计量．而

E(B2)=E(n−1nS2)=n−1nσ2≠σ2E\left(B_2\right)=E\left(\frac{n-1}{n} S^2\right)=\frac{n-1}{n} \sigma^2 \neq \sigma^2

所以 B2=1n∑i=1n(Xi−Xˉ)2B_2=\frac{1}{n} \sum_{i=1}^n\left(X_i-\bar{X}\right)^2 不是 σ2\sigma^2 的无偏估计量． 这也正是在实际应用中样本方差采用 S2=1n−1∑i=1n(Xi−Xˉ)2S^2=\frac{1}{n-1} \sum_{i=1}^n\left(X_i-\bar{X}\right)^2 而不用 B2=1n∑i=1n(Xi−Xˉ)2B_2=\frac{1}{n} \sum_{i=1}^n\left(X_i-\bar{X}\right)^2 的原因。

上述两例的结论与总体的分布类型没有关系。只要总体均值存在，样本均值总是它的无偏估计量；只要总体方差存在，样本方差总是它的无偏估计量．

本题解释：在样本的均值与方差 里，给出了方差要除以n−1n-1 而不是除以nn， 就是为了拟合 无偏性，最主要的是自由度少了1

例设总体 X∼N(μ,σ2),(X1,X2,⋯ ,Xn)X \sim N\left(\mu, \sigma^2\right),\left(X_1, X_2, \cdots, X_n\right) 为来自该总体的一个样本， 已求得：当 μ\mu 已知时， σ2\sigma^2 的矩估计量 σ^12=1n∑i=1nXi2−μ2\hat{\sigma}_1^2=\frac{1}{n} \sum_{i=1}^n X_i^2-\mu^2 ； 当 μ\mu末知时，σ2\sigma^2 的矩估计量 σ^22=1n∑i=1nXi2−(Xˉ)2=1n∑i=1n(Xi−Xˉ)2=Sn2\hat{\sigma}_2^2=\frac{1}{n} \sum_{i=1}^n X_i^2-(\bar{X})^2=\frac{1}{n} \sum_{i=1}^n\left(X_i-\bar{X}\right)^2=S_n^2. 分别讨论是 σ^12、σ^22\hat{\sigma}_1^2 、 \hat{\sigma}_2^2 的无偏性.

解

E(σ^12)=1n∑i=1nE(Xi−μ)2=1n∑i=1nE(X−μ)2=E(X−μ)2=E(X−E(X))2=D(X)=σ2\begin{aligned} E\left(\hat{\sigma}_1^2\right) & =\frac{1}{n} \sum_{i=1}^n E\left(X_i-\mu\right)^2=\frac{1}{n} \sum_{i=1}^n E(X-\mu)^2 \\ & =E(X-\mu)^2=E(X-E(X))^2=D(X)=\sigma^2 \end{aligned}

故 σ^12\hat{\sigma}_1^2 是 σ2\sigma^2 的无偏估计.

E(σ^22)=E(Sn2)=n−1nσ2≠σ2,n>2E\left(\hat{\sigma}_2^2\right)=E\left(S_n^2\right)=\frac{n-1}{n} \sigma^2 \neq \sigma^2, n>2

故 σ^22=Sn2\hat{\sigma}_2^2=S_n^2 不是 σ2\sigma^2 的无偏估计. 将 Sn2S_n^2 修正为 S2S^2 ，满足 E(S2)=σ2E\left(S^2\right)=\sigma^2 ，则 S2S^2 是 σ2\sigma^2 的无偏估计量.

上面粒子可以这么理解：假设测量5组学生每组10人，然后得到5组的平均值 172,173,172,175,174172,173,172,175,174，再用这5组均值估算全校学生的身高，现在告诉你①全校学生的真实身高是173，那我们就要估算方差是多少。②全校学生的真实身高未知，我们估算方差又是多少。对于后面这个情况因为实际均值未知，我们就用样本均值替代总体均值。

方差无偏性定理

若总体 XX 的均值 E(X)=μE(X)=\mu ，方差 D(X)=σ2D(X)=\sigma^2 ，样本为 (X1,X2,⋯ ,Xn)\left(X_1, X_2, \cdots, X_n\right) ， 则有 (1) E(Xˉ)=μE(\bar{X})=\mu, (2) E(S2)=σ2,E(Sn2)=n−1nσ2,n≥2E\left(S^2\right)=\sigma^2, E\left(S_n^2\right)=\frac{n-1}{n} \sigma^2, n \geq 2 因此，样本均值是总体均值的无偏估计，样本方差是总体方差的无偏估计，而样本的二 阶中心矩是总体方差的渐䜣无偏估计。

上面定理说明了在样本方差 S2=1n−1∑i=1n(Xi−Xˉ)2S^2=\frac{1}{n-1} \sum_{i=1}^n\left(X_i-\bar{X}\right)^2 中 1n−1\frac{1}{n-1} 的作用．对于样本的二阶中心矩 1n∑i=1n(Xi−Xˉ)2=n−1nS2\frac{1}{n} \sum_{i=1}^n\left(X_i-\bar{X}\right)^2=\frac{n-1}{n} S^2 ，由于其数学期望为 n−1nσ2≠σ2\frac{n-1}{n} \sigma^2 \neq \sigma^2 ，所以 1n∑i=1n(Xi−Xˉ)2\frac{1}{n} \sum_{i=1}^n\left(X_i-\bar{X}\right)^2 是 σ2\sigma^2 的有偏估计． 但由于 lim⁡n→∞E[1n∑i=1n(Xi−Xˉ)2]=σ2\lim _{n \rightarrow \infty} E\left[\frac{1}{n} \sum_{i=1}^n\left(X_i-\bar{X}\right)^2\right]=\sigma^2 ，因此 1n∑i=1n(Xi−Xˉ)2\frac{1}{n} \sum_{i=1}^n\left(X_i-\bar{X}\right)^2 是 σ2\sigma^2 的渐近无偏估计．为了便于与 S2S^2 对比，也将样本的二阶中心矩 1n∑i=1n(Xi−Xˉ)2\frac{1}{n} \sum_{i=1}^n\left(X_i-\bar{X}\right)^2 记为 Sn2S_n^2 ，即 Sn2=1n∑i=1n(Xi−Xˉ)2S_n^2=\frac{1}{n} \sum_{i=1}^n\left(X_i-\bar{X}\right)^2 。

例 设总体 X∼P(λ)X \sim P(\lambda) ，对任意的常数 c∈(0,1)c \in(0,1) ，问 cXˉ+(1−c)S2c \bar{X}+(1-c) S^2是否为 λ\lambda 的无偏估计？

解 由于 X∼P(λ)X \sim P(\lambda) ，故 EX=DX=λE X=D X=\lambda ，由定理知道， Xˉ\bar{X} 和 S2S^2 均为 λ\lambda 的无偏估计．又因为 c+(1−c)=1c+(1-c)=1 ， cXˉ+(1−c)S2c \bar{X}+(1-c) S^2 为 λ\lambda 的无偏估计．

例题

例 设总体 X∼B(1,p),(X1,X2,⋯ ,Xn)X \sim B(1, p),\left(X_1, X_2, \cdots, X_n\right) 为来自总体 XX 的样本，试问 p^=Xˉ\hat{p}=\bar{X} 是否为未知参数 pp 的无偏估计？

解 由于 Ep^=EXˉ=EX=pE \hat{p}=E \bar{X}=E X=p ，所以 p^=Xˉ\hat{p}=\bar{X} 是 pp 的无偏估计．

例 设总体 XX 的概率密度为

f(x)={2x3θ2,θ<x<2θ, 0, 其他, f(x)= \begin{cases}\frac{2 x}{3 \theta^2}, & \theta<x<2 \theta, ~ \\ 0, & \text { 其他, }\end{cases}

其中 θ\theta 是未知参数．X1,X2,⋯ ,XnX_1, X_2, \cdots, X_n 为来自总体 XX 的简单样本，选择适当的常数 cc ，使 c∑i=1nXi2c \sum_{i=1}^n X_i^2 是 θ2\theta^2 的无偏估计量． （解）由于 c∑i=1nXi2c \sum_{i=1}^n X_i^2 是 θ2\theta^2 的无偏估计量，所以

E(c∑i=1nXi2)=θ2E\left(c \sum_{i=1}^n X_i^2\right)=\theta^2

而

E(c∑i=1nXi2)=c∑i=1nE(Xi2)=c∑i=1nE(X2)E(X2)=∫θ2θx22x3θ2dx=52θ2\begin{aligned} E\left(c \sum_{i=1}^n X_i^2\right) & =c \sum_{i=1}^n E\left(X_i^2\right)=c \sum_{i=1}^n E\left(X^2\right) \\ E\left(X^2\right) & =\int_\theta^{2 \theta} x^2 \frac{2 x}{3 \theta^2} d x=\frac{5}{2} \theta^2 \end{aligned}

所以

E(c∑i=1nXi2)=52cnθ2=θ2E\left(c \sum_{i=1}^n X_i^2\right)=\frac{5}{2} c n \theta^2=\theta^2

故

c=25nc=\frac{2}{5 n}
上一章4._点估计_极大似然估计
下一章6._有效性